
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Локальная предельная теорема Муавра-Лапласа.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть производится n независимых испытаний. В каждом испытании возможны два исхода: либо наступит событие A, либо
равномерно для тех m, для которых
находится в каком либо конечном интервале. Практическое значение теоремы заключается в том, что она позволяет вычислить биноминальные вероятности Р(n,m) при большом значении n. Теоретическое значение этой теоремы следующее: дискретное биноминальное распределение при больших значениях n можно заменить непрерывным нормальным распределением т.е. количество переходит в качество. Пример 15. Вероятность того, что станок-автомат произведет годную деталь равна 8/9. За смену изготавливается 280 деталей. Определить вероятность того, что среди них 20 бракованных. Решение. n=280, m=20, p=8/9, q=1/9. По формуле Бернулли эту вероятность вычислит трудно, поэтому используем локальную теорему Муавра-Лапласа:
где
Интегральная предельная теорема Муавра-Лапласа Пусть производится n независимых испытаний. В каждом испытании возможны два исхода: либо наступит событие A, либо
где Эта теорема применяется при вычислении вероятностей
Пример 16. В страховой компании застраховано 10000 автомобилей. Вероятность поломки любого автомобиля в результате аварии равна 0,006. Каждый владелец застрахованной машины платит в год 12 грн. страховых и в случае ее поломки в результате аварии получает от компании 1000 грн. Найти вероятность того, что по истечении года работы компания потерпит убыток. Событие A – компания потерпит убыток, n = 10000, p(A) = 0,006, q = 0,994. Ежегодно кампания получает от клиентов S= 10000*12=120000 грн. Обозначим m – число автомобилей, потерпевших аварию. Тогда компания должна выплатить сумму, равную R = m Требуется найти Р(А) = P(R > S) = P(1000m > 120000) = P(m>120). Перейдем к противоположному событию Ā – компания не потерпит убытки, и найдем вероятность Применим интегральную теорему Муавра-Лапласа
Таким образом, P(A) = 1-Р(Ā) = 1 - 1=0, т.е. вероятность того, что компания потерпит убыток равна нулю.
Закон больших чисел Закон больших чисел - это есть целый ряд теорем, которые устанавливают условия сходимости среднего арифметического случайных величин к среднему арифметическому их математических ожиданий. Рассмотрим последовательность случайных величин Последовательность сходится по вероятности к некоторому числу b при n→∞, если
Теорема Чебышева Пусть
Это утверждение можно записать иначе, в эквивалентной форме.
которую используют при решении прикладных задач. В частности, отсюда следует утверждение: Если
или в эквивалентной форме
Теорема Бернулли. Применим теорему Хинчина к случайной величине
Вероятности р(А) = р, р ( n → ∞ и для любого
или в эквивалентной форме
Смысл этой теоремы заключается в том, что относительная частота появления события по вероятности сходится к вероятности этого события. Обобщением теоремы Бернулли на случай, когда испытания происходят при неодинаковых условиях, что вызывает изменение вероятности появлений события А в каждом испытании, является теорема Пуассона.
Теорема Пуассона. Рассмотрим последовательность n независимых испытаний, в каждом из которых событие А наступает с вероятностью р как и в предыдущем случае, получим М (
Запишем утверждение теоремы Пуассона в эквивалентной форме
где Рассмотрим пример на применение закона больших чисел. Пример 17. из 100 изделий, отправляемых в сборочный цех, было подвергнуто обследованию 200, отобранных случайным образом. Среди них оказалось 25 бракованных. Приняв долю бракованных изделий среди отобранных, за вероятность изготовления бракованного изделия, оценить вероятность того, что во всей партии бракованных изделий окажется в пределах от 15% до 20%. Для решения задачи используем неравенство (36). Вероятность изготовления бракованного изделия по условию Р(0,10 Р(0,10 – 0,125
Первое неравенство Чебышева. Если случайная величина
В частности, если
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1019; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.012 с.) |

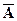 . Если вероятность наступления события постоянна и равна р (0<p<1), то вероятность
. Если вероятность наступления события постоянна и равна р (0<p<1), то вероятность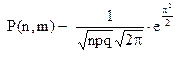 =
=  при
при 

 ,
, , значение
, значение  - определено по таблице Приложения 1, φ(-2,11) = φ(2,11) = 0,043.
- определено по таблице Приложения 1, φ(-2,11) = φ(2,11) = 0,043. ,
, - функция Лапласа.
- функция Лапласа. .
. . (32)
. (32) 1000 грн.
1000 грн.

 .
.
 c, i=1,2..,n Тогда при n → ∞ и для любого
c, i=1,2..,n Тогда при n → ∞ и для любого 

 , (33)
, (33) ,
, (34)
(34) = m – число появлений события А в серии n независимых испытаний. Представим эту случайную величину в виде суммы попарно независимых, одинаково распределенных случайных величин
= m – число появлений события А в серии n независимых испытаний. Представим эту случайную величину в виде суммы попарно независимых, одинаково распределенных случайных величин  =
= 
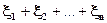 (35)
(35)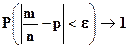 ,
, . (36)
. (36) , i=1,2,…n. Рассуждая также,
, i=1,2,…n. Рассуждая также, , где
, где  =
=  , т.е. относительная частота появления события А сходится по вероятности к средней арифметической вероятностей этого события в каждом испытании.
, т.е. относительная частота появления события А сходится по вероятности к средней арифметической вероятностей этого события в каждом испытании. ,
,  (37)
(37) .Требуется найти вероятность
.Требуется найти вероятность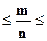 0,15). Вычтем в каждой части неравенства р, получим
0,15). Вычтем в каждой части неравенства р, получим 0,15– 0,125) = Р(– 0,025
0,15– 0,125) = Р(– 0,025  .
. , то
, то 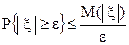 . (38)
. (38) и существует
и существует  , то
, то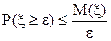 . (39)
. (39)


