
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция Эйлера. Теоремы Эйлера, Ферма и др.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема. Пусть
Утверждение теоремы вытекает из приводимых ниже лемм 1, 2. Лемма 1. Пусть
Доказательство. Среди чисел Лемма 2. Если нод ( Доказательство. Для
попарно не пересекающихся подмножеств
Удалим из Теорема Эйлера.
Доказательство. Пусть
…
где
Так как нод Следствие (Малая теорема Ферма). Если
Доказательство. Достаточно учесть, что Следствие. Если
Доказательство. Если
Теорема Эйлера допускает следующее обобщение: Теорема Кармайкла. Для любых взаимно простых чисел
где
Замечание. Для чисел Доказательство. См. Приложение. ∎ Следующее утверждение является обращением теоремы Ферма: Теорема Люка ( 1876 ). Натуральное число (Доказательство этой теоремы откладывается.) Из Малой теоремы Ферма следует, что если нод
Такие (составные) числа называют псевдопростыми. Теорема Чиполлы Доказательство. Положим
− целые числа. Имеем
где
Допустим, что нод
Пример. Для Замечание. Число Приведём одно утверждение, используемое в криптографии (в алгоритме Теорема. Пусть
является взаимно однозначным на множестве
где Доказательство. Достаточно показать, что
рассматривая случаи: 1) В первом случае имеем:
а во втором случае:
(здесь Китайская теорема об остат к ах. Число
Китайская теорема об остат к ах. Пусть [ (1) причём единственное. Доказательство. Построим искомое
Нетрудно проверить, что число
То
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 633; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.44.46 (0.007 с.) |

 каноническое разложение натурального числа
каноническое разложение натурального числа  . Тогда
. Тогда .
.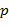 − простое число,
− простое число,  . Тогда
. Тогда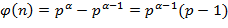 .
. ,
,  ,…,
,…,  имеется в точности
имеется в точности  чисел, кратных
чисел, кратных 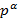 . ∎
. ∎ ,
, 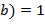 , то
, то  .
.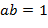 утверждение леммы очевидно. Пусть
утверждение леммы очевидно. Пусть 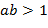 . Рассмотрим множество
. Рассмотрим множество 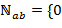 ,
, 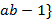 . Его можно представить как объединение
. Его можно представить как объединение
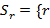 ,
, 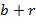 ,
,  ,…,
,…,  ,
,  ,
, 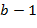 .
.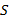 подмножества
подмножества 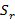 , для которых нод
, для которых нод 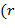 ,
, 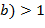 . В результате в
. В результате в 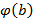 подмножеств
подмножеств 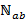 , взаимно простые с
, взаимно простые с 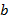 . Далее, любое из подмножеств
. Далее, любое из подмножеств  чисел, взаимно простых с
чисел, взаимно простых с  . Всего же во множестве
. Всего же во множестве  чисел. С другой стороны, в исходном множестве
чисел. С другой стороны, в исходном множестве 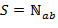 содержится
содержится 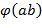 чисел, взаимно простых с
чисел, взаимно простых с 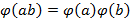 . ∎
. ∎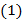 нод
нод 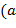 ,
, 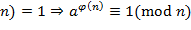 .
.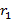 ,
,  ,…,
,…,  , где
, где  ,− числа, образуют приведённую систему вычетов по модулю
,− числа, образуют приведённую систему вычетов по модулю 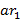 ,
,  ,…,
,…, 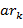 также образуют приведённую систему вычетов по модулю
также образуют приведённую систему вычетов по модулю 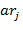 сравнимо по модулю
сравнимо по модулю 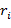 , и обратно. Следовательно, имеет место система сравнений
, и обратно. Следовательно, имеет место система сравнений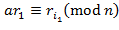 ,
, 
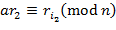 ,
, ,
,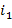 ,
, 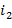 , …,
, …, 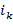 − некоторая перестановка индексов
− некоторая перестановка индексов  , …,
, …,  . Перемножая левые и правые части этих сравнений, получаем
. Перемножая левые и правые части этих сравнений, получаем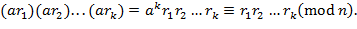
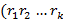 ,
,  , то левую и правую части последнего сравнения можно сократить на
, то левую и правую части последнего сравнения можно сократить на 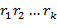 . В результате получим
. В результате получим 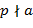 , то
, то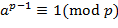 .
.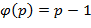 , и применить теорему Эйлера.∎
, и применить теорему Эйлера.∎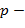 простое число, то
простое число, то для любых
для любых 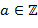 ,
,  .
.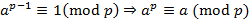 . Если
. Если  , то последнее сравнение заведомо выполняется. Но тогда
, то последнее сравнение заведомо выполняется. Но тогда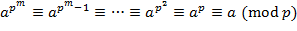 . ∎
. ∎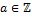 ,
, 
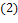
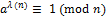 ,
,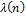 − функция Кармайкла, определяемая следующим образом:
− функция Кармайкла, определяемая следующим образом: ,
, 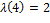 ;
;  , если
, если 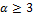 ;
;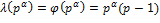 , если
, если  − нечетное простое число;
− нечетное простое число; ,…,
,…, 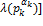 , если
, если 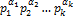 − каноническое разложение числа
− каноническое разложение числа  .
. или
или 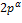 , где
, где 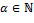 , имеет место равенство
, имеет место равенство 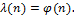 Во всех остальных случаях
Во всех остальных случаях  и для них соотношение (2) улучшает теорему Эйлера.
и для них соотношение (2) улучшает теорему Эйлера. такое, что
такое, что 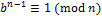 , но
, но  для любого простого делителя
для любого простого делителя  числа
числа  .
.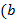 ,
, 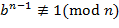 , то
, то 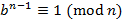 .
. . Существует бесконечно много
. Существует бесконечно много 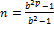 , где
, где 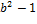 , и отметим, что
, и отметим, что 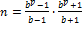 , а
, а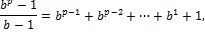
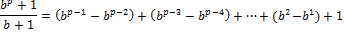
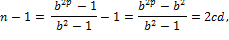
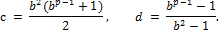
 ,
,  . Тогда
. Тогда 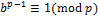 . Поскольку
. Поскольку 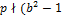 ), то
), то 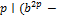 1) и
1) и 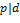 . Если же нод
. Если же нод 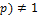 , то
, то  и
и  . В любом случае
. В любом случае 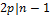 , и
, и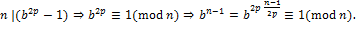 ∎
∎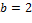 и
и  получим
получим  и
и 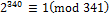 .
.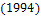 , что множество чисел Кармайкла бесконечно. Первое такое число равно
, что множество чисел Кармайкла бесконечно. Первое такое число равно 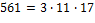 .
. ):
): ,
,  − любое число, взаимно простое с
− любое число, взаимно простое с  . Тогда отображение
. Тогда отображение
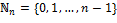 , причем обратным к нему является отображение
, причем обратным к нему является отображение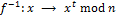 ,
,

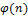 − число, удовлетворяющее сравнению
− число, удовлетворяющее сравнению  .
. ,
,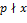 и
и 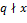 ; 2)
; 2)  , т.е.
, т.е. 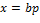 для некоторого
для некоторого 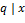 (этот случай аналогичен предыдущему, поэтому не рассматривается). Отметим, что
(этот случай аналогичен предыдущему, поэтому не рассматривается). Отметим, что 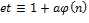 для некоторого
для некоторого  .
. ,
,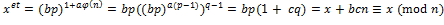
 некоторое целое). ∎
некоторое целое). ∎ называется мультипликативным обратным к
называется мультипликативным обратным к 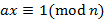 . Очевидно, что
. Очевидно, что 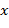 существует тогда и только тогда, когда нод
существует тогда и только тогда, когда нод  . В этом случае в качестве
. В этом случае в качестве 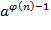 по модулю
по модулю 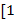 ,
,  содержится в точности одно такое
содержится в точности одно такое 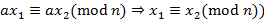 ; соответствующее
; соответствующее  . Другой способ вычисления
. Другой способ вычисления  ) основан на использовании расширенного алгоритма Евклида, в котором наряду с вычислением нод
) основан на использовании расширенного алгоритма Евклида, в котором наряду с вычислением нод  также вычисляются числа
также вычисляются числа  такие, что
такие, что 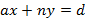 .
.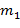 ,…,
,…, 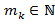 − любые попарно взаимно простые числа;
− любые попарно взаимно простые числа; 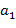 ,…,
,…,  − любые числа;
− любые числа; 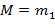 …
…  . Тогда в интервале
. Тогда в интервале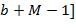 содержится число
содержится число 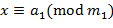 ,…,
,…,  ,
,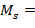
 =
= 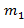 …
… 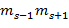 …
…  =
= 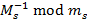 (число
(число 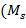 ,
, 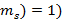 ,
, 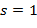 ,…,
,…, 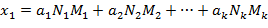 .
. удовлетворяет системе сравнений
удовлетворяет системе сравнений 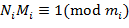 и
и  при
при  ,
, 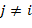 . Если
. Если  и
и  удовлетворяет
удовлетворяет  , где
, где 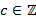 , удовлетворяет
, удовлетворяет 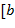 ,
,  . Поскольку число
. Поскольку число  удовлетворяет системе сравнений
удовлетворяет системе сравнений , …,
, …,  ,
,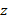 делится без остатка на
делится без остатка на 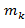 , и, следовательно, на
, и, следовательно, на 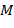 . Так как
. Так как  , то
, то  и
и 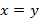 . Значит, в указанном интервале содержится в точности одно число, удовлетворяющее системе сравнений
. Значит, в указанном интервале содержится в точности одно число, удовлетворяющее системе сравнений 


