Деление многочленов над целостным кольцом.
Пусть  − целостное кольцо. − целостное кольцо.
Теорема. (Об однозначности деления с остатком.) Пусть  − многочлен с обратимым старшим коэффициентом. Тогда любому многочлену − многочлен с обратимым старшим коэффициентом. Тогда любому многочлену  сопоставляется одна и только одна пара многочленов сопоставляется одна и только одна пара многочленов 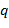 , ,  , для которых , для которых
 , , 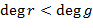 . .
Доказательство. Пусть
 , ,
 , ,
где 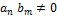 и существует и существует  обратный элемент для обратный элемент для  . Применим индукцию по . Применим индукцию по  . Если . Если  и и 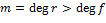 , то положим , то положим  , ,  ; если ; если  , то положим , то положим  , ,  . Допустим, что утверждение теоремы доказано для всех многочленов . Допустим, что утверждение теоремы доказано для всех многочленов  степени степени  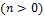 . Можно считать, что . Можно считать, что 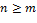 , поскольку в противном случае , поскольку в противном случае  , ,  . Коль скоро это так, то . Коль скоро это так, то
 , ,
где  . По предположению индукции существуют . По предположению индукции существуют  и и  такие, что такие, что  , , 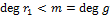 . Положив . Положив   и и  , получим искомую пару многочленов. , получим искомую пару многочленов.
Для доказательства единственности  и и  предположим, что предположим, что
 . .
Тогда  . Так как . Так как  целостное кольцо, то целостное кольцо, то 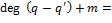
 . Но это возможно только при . Но это возможно только при  и и 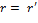 . ∎ . ∎
Многочлены 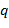 и и  называют соответственно частным и остатком от деления называют соответственно частным и остатком от деления  на на  . Если . Если  , то говорят, что , то говорят, что  делится на делится на  , или , или  кратно кратно  , и пишут , и пишут 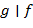 . Если . Если 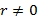 , то пишут , то пишут 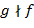 . Операции вычисления частного и остатка обозначим как div и mod, так что . Операции вычисления частного и остатка обозначим как div и mod, так что  и и  . Сам процесс вычисления частного и остатка . Сам процесс вычисления частного и остатка 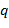 и и  называют евклидовым делением. Если называют евклидовым делением. Если  − поле, то деление на − поле, то деление на  всегда возможно, поскольку в поле все ненулевые элементы обратимы. всегда возможно, поскольку в поле все ненулевые элементы обратимы.
Следствие. В кольце  многочленов над полем многочленов над полем  все идеалы − главные. все идеалы − главные.
Доказательство. Пусть 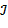 − любой ненулевой идеал в − любой ненулевой идеал в  . Выберем в . Выберем в 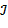 ненулевой многочлен ненулевой многочлен  минимальной степени, и пусть минимальной степени, и пусть  − любой другой многочлен из − любой другой многочлен из 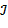 . Разделим . Разделим  на на  , т.е. представим его в виде , т.е. представим его в виде  , , 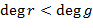 . Так как . Так как  и и
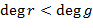 , то ввиду выбора , то ввиду выбора  заключаем, что заключаем, что  − нулевой многочлен. Отсюда следует, что множество − нулевой многочлен. Отсюда следует, что множество 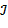 состоит в точности из многочленов, кратных состоит в точности из многочленов, кратных  . Значит, . Значит, 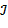 − главный идеал. ∎ − главный идеал. ∎
Замечание. Для колец многочленов от нескольких переменных данное утверждение неверно. Идеалы в  , ,  , ,  не исчерпываются главными. Пример см. Кострикин, с. 217. ∎ не исчерпываются главными. Пример см. Кострикин, с. 217. ∎
НОД и НОК в кольце 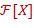 , где , где  − поле. − поле.
Определение. Пусть  , ,  − многочлены, не являющиеся одновременно нулевыми. Многочлен − многочлены, не являющиеся одновременно нулевыми. Многочлен  наибольшей степени такой, что наибольшей степени такой, что  и и  , называется наибольшим общим делителем многочленов , называется наибольшим общим делителем многочленов  и и  , и обозначается через нод , и обозначается через нод  , ,  . .
Отметим следующие свойства, используя которые нетрудно получить алгоритм вычисления нод  , ,  : :
1) нод  , ,  нод нод  , ,  ; ;
2) нод  , ,  ; ;
3) если  , то нод , то нод  , ,  нод нод  , ,  , где , где  . .
Алгоритм Евклида:
пока  и и  делать делать
если 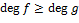 то то 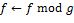 иначе иначе  ; ; 
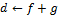 . .
По аналогии с нод  , ,  вводится дуальное понятие − наименьшее общее кратное вводится дуальное понятие − наименьшее общее кратное  нок нок  , ,  , где , где  , − многочлен наименьшей степени такой, что , − многочлен наименьшей степени такой, что 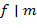 и и  . .
Замечание. Если нод 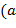 , , 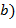 целых чисел целых чисел  , , 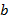 определён однозначно, то определён однозначно, то 
нод 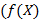 , ,  для многочленов для многочленов  и и  определён с точностью до умножения на ненулевой элемент определён с точностью до умножения на ненулевой элемент 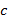 поля ℱ. Иными словами, наряду с поля ℱ. Иными словами, наряду с  многочлен многочлен  также является наибольшим общим делителем многочленов также является наибольшим общим делителем многочленов  и и  . Чтобы устранить неоднозначность, выберем среди многочленов . Чтобы устранить неоднозначность, выберем среди многочленов  унитарный, т.е. тот, у которого старший коэффициент равен единице. Такое же уточнение сделаем и относительно наименьшего общего кратного. унитарный, т.е. тот, у которого старший коэффициент равен единице. Такое же уточнение сделаем и относительно наименьшего общего кратного.
Если нод  , , 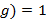 , то многочлены , то многочлены  и и  будем называть взаимно простыми. будем называть взаимно простыми.
Рассмотрим множество многочленов   , , 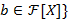 . Нетрудно проверить, что . Нетрудно проверить, что 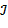 − идеал в − идеал в  . Согласно теореме, . Согласно теореме, 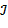 − главный идеал, т.е. − главный идеал, т.е.  для некоторого многочлена для некоторого многочлена 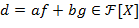 . Используя алгоритм деления, запишем многочлен . Используя алгоритм деления, запишем многочлен  в виде в виде  , где , где  . Ввиду . Ввиду  , , 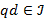 имеет место включение имеет место включение
 . .
Отсюда следует, что  , и, следовательно, , и, следовательно,  . Аналогично доказывается, что . Аналогично доказывается, что  . Пусть теперь . Пусть теперь  любой делитель многочленов любой делитель многочленов  и и  . Тогда . Тогда
 , ,   . .
Очевидно, что  обладает всеми свойствами наибольшего общего делителя многочленов обладает всеми свойствами наибольшего общего делителя многочленов  и и  . Значит, . Значит, 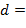 нод нод  , ,  . Таким образом, доказана следующая . Таким образом, доказана следующая
Теорема.
нод ( , , 
для некоторых многочленов  , ,  . .
Определение. Многочлен 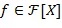 степени степени  называется неприводимым в называется неприводимым в  (или неприводимым над полем (или неприводимым над полем  ), если он не делится ни на какой многочлен ), если он не делится ни на какой многочлен  степени степени  . .
Теорема. Множество унитарных неприводимых многочленов над любым полем  бесконечно. бесконечно.
Это утверждение доказывается так же, как и соответствующее утверждение о бесконечности множества простых чисел в кольце  . ∎ . ∎
Так как множество многочленов заданной степени над конечным полем − конечное число, то справедливо следующая
Теорема. Над конечным полем существуют неприводимые многочлены сколь угодно высокой степени.
Замечание. На самом деле над конечным полем существуют неприводимые многочлены любой степени. Это же справедливо и для поля  рациональных чисел. С другой стороны, над полем ℂ комплексных чисел существуют неприводимые многочлены только первой и второй степени. рациональных чисел. С другой стороны, над полем ℂ комплексных чисел существуют неприводимые многочлены только первой и второй степени.
Неприводимые многочлены играют важную роль в кольце  , такую же, как и простые числа в кольце , такую же, как и простые числа в кольце  . .
Лемма. Пусть 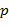 , ,  , ,  − многочлены над полем − многочлены над полем  . Тогда, если . Тогда, если 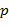 − неприводимый над полем − неприводимый над полем  многочлен и многочлен и 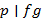 , то либо , то либо  , либо , либо  (либо и то, и другое). (либо и то, и другое).
Теорема. (Основная теорема арифметики кольца 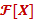 об однозначности разложения на множители.) Каждый многочлен положительной степени об однозначности разложения на множители.) Каждый многочлен положительной степени 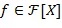 ( ( − поле) модет быть представлен в виде произведения − поле) модет быть представлен в виде произведения
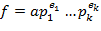 , ,
где  , ,  ,…, ,…,  − различные унитарные неприводимые многочлены из − различные унитарные неприводимые многочлены из  , а , а  ,…, ,…,  − натуральные числа. Это разложение однозначно с точностью до порядка сомножителей. Оно называется каноническим разложен ием многочлена − натуральные числа. Это разложение однозначно с точностью до порядка сомножителей. Оно называется каноническим разложен ием многочлена  в кольце в кольце  . .
Доказательство этих утверждений аналогично доказательствам соответствующих утверждений о разложении чисел на простые множители в кольце  . ∎ . ∎
Если
 , ,  , ,
где  , , 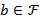 , ,  ; ;  ,…, ,…,  − различные неприводимые над − различные неприводимые над  многочлены; многочлены;  ,…, ,…,  , ,  ,…, ,…, 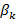 − неотрицательные целые числа, то − неотрицательные целые числа, то
нод  , ,  , нок , нок  , ,  , ,
где 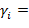 min min  , ,  }, },  , ,  , ,  , ,  , …, , …,  . Отсюда следует, что . Отсюда следует, что
 нод нод  , , 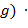 нок нок  , , 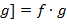 . .
Теорема. Пусть 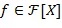 . Факторкольцо . Факторкольцо  является полем тогда и только тогда, когда является полем тогда и только тогда, когда  − неприводимый многочлен над полем − неприводимый многочлен над полем  . .
Доказательство. Элементами кольца  являются классы вычетов являются классы вычетов  , где , где 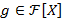 . Классы вычетов . Классы вычетов  и и  совпадают тогда и только тогда, когда совпадают тогда и только тогда, когда  , т.е. и при дении на дают один и тот же остаток. Поэтому различные элементы в , т.е. и при дении на дают один и тот же остаток. Поэтому различные элементы в  можно описать явно, а именно это те классы можно описать явно, а именно это те классы  , где , где  пробегает множество многочленов из пробегает множество многочленов из  степени < степени <  . Отметим, что роль нуля и единицы в . Отметим, что роль нуля и единицы в  играют классы вычетов играют классы вычетов 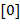 и и  , где , где  и и  − нуль и единица поля − нуль и единица поля  . .
Предположим, что  не является неприводимым многочленом. Тогда не является неприводимым многочленом. Тогда  для некоторых многочленов для некоторых многочленов  , ,  степени степени  , ,  . Так как . Так как  и и 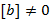 и и
 , то , то  не может быть полем, поскольку содержит делители нуля. не может быть полем, поскольку содержит делители нуля.
Теперь предположим, что  − неприводимый над − неприводимый над  многочлен степени многочлен степени  . Пусть . Пусть 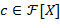 − любой ненулевой многочлен степени − любой ненулевой многочлен степени  (так что (так что  − произвольный элемент кольца − произвольный элемент кольца  ). Многочлены ). Многочлены  и и 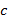 , очевидно, взаимно просты. Согласно теореме нод ( , очевидно, взаимно просты. Согласно теореме нод ( , ,  ) =1= ) =1= 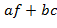 для некоторых для некоторых  , ,  . Но тогда . Но тогда
 , ,
т.е. элемент  имеет обратный, а именно имеет обратный, а именно  . Значит, . Значит,  − поле. ∎ − поле. ∎
Корни многочленов
Пусть 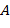 − подкольцо с единицей целостного кольца − подкольцо с единицей целостного кольца  . .
Определение. Элемент  называется корнем (или нулём) многочлена называется корнем (или нулём) многочлена  , если , если  . (Говорят также, что . (Говорят также, что  − корень уравнения − корень уравнения  .) .)
Замечание. Переход от кольца 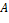 к кольцу к кольцу 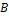 (для которого (для которого 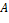 является собственным подкольцом) обычно обусловлен следующим обстоятельством. Многочлен является собственным подкольцом) обычно обусловлен следующим обстоятельством. Многочлен  может не иметь корней в может не иметь корней в 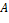 . С другой стороны, ввиду . С другой стороны, ввиду  , многочлен , многочлен  можно рассматривать как элемент кольца можно рассматривать как элемент кольца  . При этом . При этом  может иметь корни в может иметь корни в 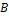 . Например, многочлен . Например, многочлен  не имеет корней в не имеет корней в 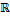 , но имеет два корня в , но имеет два корня в  (именно: (именно:  и – и – 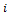 , где , где  ). Как бы там ни было, мы рассмотрим сначала случай ). Как бы там ни было, мы рассмотрим сначала случай  . .
Теорема Безу. Элемент  является корнем многочлена является корнем многочлена 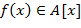 тогда и только тогда, когда тогда и только тогда, когда 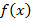 делится на делится на  . .
Доказательство. Многочлен 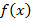 может быть записан в виде может быть записан в виде
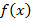 = =   + +  , deg , deg  < deg < deg  = 1. = 1.
Так как  , то , то  тогда и только тогда, когда тогда и только тогда, когда  − нулевой многочлен. ∎ − нулевой многочлен. ∎
Определение. Элемент  называется корнем кратности называется корнем кратности  (или - кратным корнем) многочлена (или - кратным корнем) многочлена  , если , если  делится на делится на 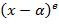 , но не делится на , но не делится на 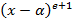 . При . При 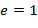 корень корень  называется простым, а при называется простым, а при 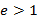 − кратным. − кратным.
Очевидно, что  является является  -кратнымкорнем многочлена -кратнымкорнем многочлена 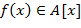 тогда и только тогда, когда тогда и только тогда, когда 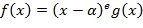 , где , где 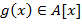 и и  . Так как . Так как 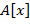 − целостное кольцо, то deg − целостное кольцо, то deg  . .
Теорема. Если  ,…, ,…, 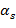 − различные корни ненулевого многочлена − различные корни ненулевого многочлена 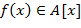 кратностей кратностей  ,…, ,…, 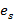 соответственно, то соответственно, то
(1) 
для некоторого многочлена  такого, что такого, что 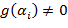 , ,  ,…, ,…, 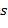 . При этом . При этом
(2) 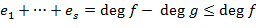 . .
Доказательство. Применим индукцию по  . При . При  доказывать нечего. Пусть доказано, что доказывать нечего. Пусть доказано, что

для некоторых  и многочлена и многочлена  такого, что такого, что  , ,  ,…, ,…,  .Подстановка .Подстановка 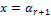 даёт даёт
 . .
Так как 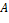 − целостное кольцо и − целостное кольцо и  , ,  ,…, ,…,  , то , то  . Пусть . Пусть  , г , г  (и, очевидно, (и, очевидно,  , ,  ,…, ,…,  ). Тогда ). Тогда
 , ,
где  . Допустим, что . Допустим, что 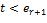 . Тогда, используя закон сокращения в целостном кольце, получаем . Тогда, используя закон сокращения в целостном кольце, получаем  , что, однако, невозможно ввиду , что, однако, невозможно ввиду
 и и  . .
Следовательно,  . Аналогично доказываем, что . Аналогично доказываем, что  . Поэтому . Поэтому  и и
 , ,
где  , ,  ,…, ,…,  . Это и требовалось показать. Наконец, неравенство (2) непосредственно вытекает из (1). ∎ . Это и требовалось показать. Наконец, неравенство (2) непосредственно вытекает из (1). ∎
Замечание. Без предположения о целостности кольца 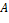 теорема неверна. Например, если теорема неверна. Например, если  ( ( − кольцо целых чисел по модулю 8), то − кольцо целых чисел по модулю 8), то  = =   ; разложение ; разложение  также неоднозначно: также неоднозначно:
 . .
Из теоремы вытекает
Следствие. Ненулевой многочлен 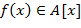 степени степени  имеет, самое большее, имеет, самое большее,  корней. Два многочлена корней. Два многочлена  , ,  степени степени  , принимающие одинаковые значения при подстановке , принимающие одинаковые значения при подстановке  + 1 различных элементов из + 1 различных элементов из 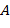 , равны: , равны:  = =  . .
Доказательство. Если допустить, что многочлен  имеет не менее имеет не менее 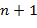 корней, то возникает противоречие с неравенством в (2). Если корней, то возникает противоречие с неравенством в (2). Если  , то многочлен , то многочлен  имеет степень имеет степень  , но не менее , но не менее 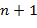 корней, что невозможно. ∎ корней, что невозможно. ∎
|



 − целостное кольцо.
− целостное кольцо. − многочлен с обратимым старшим коэффициентом. Тогда любому многочлену
− многочлен с обратимым старшим коэффициентом. Тогда любому многочлену  сопоставляется одна и только одна пара многочленов
сопоставляется одна и только одна пара многочленов 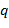 ,
,  , для которых
, для которых ,
, 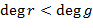 .
. ,
, ,
,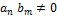 и существует
и существует  обратный элемент для
обратный элемент для  . Применим индукцию по
. Применим индукцию по  . Если
. Если  и
и 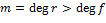 , то положим
, то положим  ,
,  ; если
; если  , то положим
, то положим  ,
,  . Допустим, что утверждение теоремы доказано для всех многочленов
. Допустим, что утверждение теоремы доказано для всех многочленов  степени
степени 
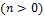 . Можно считать, что
. Можно считать, что 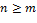 , поскольку в противном случае
, поскольку в противном случае  ,
,  ,
, . По предположению индукции существуют
. По предположению индукции существуют  и
и  такие, что
такие, что  ,
, 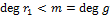 . Положив
. Положив 
 , получим искомую пару многочленов.
, получим искомую пару многочленов. и
и  предположим, что
предположим, что .
. . Так как
. Так как  целостное кольцо, то
целостное кольцо, то 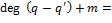
 . Но это возможно только при
. Но это возможно только при  и
и 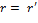 . ∎
. ∎ на
на  . Если
. Если  , то говорят, что
, то говорят, что 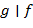 . Если
. Если 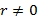 , то пишут
, то пишут 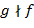 . Операции вычисления частного и остатка обозначим как div и mod, так что
. Операции вычисления частного и остатка обозначим как div и mod, так что  и
и  . Сам процесс вычисления частного и остатка
. Сам процесс вычисления частного и остатка  − поле, то деление на
− поле, то деление на  многочленов над полем
многочленов над полем  все идеалы − главные.
все идеалы − главные. − любой ненулевой идеал в
− любой ненулевой идеал в  и
и ,
,  ,
,  не исчерпываются главными. Пример см. Кострикин, с. 217. ∎
не исчерпываются главными. Пример см. Кострикин, с. 217. ∎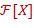 , где
, где  − поле.
− поле. − многочлены, не являющиеся одновременно нулевыми. Многочлен
− многочлены, не являющиеся одновременно нулевыми. Многочлен  наибольшей степени такой, что
наибольшей степени такой, что  и
и  , называется наибольшим общим делителем многочленов
, называется наибольшим общим делителем многочленов  ,
,  .
. нод
нод  ,
,  ;
; ,
,  ;
; , то нод
, то нод  ,
,  и
и  делать
делать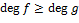 то
то 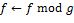 иначе
иначе  ;
; 
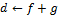 .
. нок
нок  ,
,  , где
, где  , − многочлен наименьшей степени такой, что
, − многочлен наименьшей степени такой, что 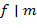 и
и  .
.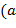 ,
, 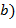 целых чисел
целых чисел  ,
, 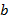 определён однозначно, то
определён однозначно, то 
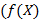 ,
,  для многочленов
для многочленов  определён с точностью до умножения на ненулевой элемент
определён с точностью до умножения на ненулевой элемент 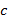 поля ℱ. Иными словами, наряду с
поля ℱ. Иными словами, наряду с  многочлен
многочлен  также является наибольшим общим делителем многочленов
также является наибольшим общим делителем многочленов 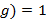 , то многочлены
, то многочлены 
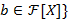 . Нетрудно проверить, что
. Нетрудно проверить, что  для некоторого многочлена
для некоторого многочлена 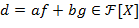 . Используя алгоритм деления, запишем многочлен
. Используя алгоритм деления, запишем многочлен  , где
, где  . Ввиду
. Ввиду 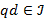 имеет место включение
имеет место включение .
. любой делитель многочленов
любой делитель многочленов  ,
, 
 .
. обладает всеми свойствами наибольшего общего делителя многочленов
обладает всеми свойствами наибольшего общего делителя многочленов 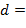 нод
нод  . Таким образом, доказана следующая
. Таким образом, доказана следующая .
.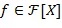 степени
степени  называется неприводимым в
называется неприводимым в  степени
степени  .
. . ∎
. ∎ рациональных чисел. С другой стороны, над полем ℂ комплексных чисел существуют неприводимые многочлены только первой и второй степени.
рациональных чисел. С другой стороны, над полем ℂ комплексных чисел существуют неприводимые многочлены только первой и второй степени.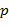 ,
, 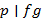 , то либо
, то либо  , либо
, либо  (либо и то, и другое).
(либо и то, и другое).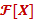 об однозначности разложения на множители.) Каждый многочлен положительной степени
об однозначности разложения на множители.) Каждый многочлен положительной степени 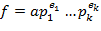 ,
, ,
,  ,…,
,…,  − различные унитарные неприводимые многочлены из
− различные унитарные неприводимые многочлены из  ,…,
,…,  − натуральные числа. Это разложение однозначно с точностью до порядка сомножителей. Оно называется каноническим разложен ием многочлена
− натуральные числа. Это разложение однозначно с точностью до порядка сомножителей. Оно называется каноническим разложен ием многочлена  ,
,  ,
,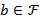 ,
,  ;
;  ,…,
,…,  ,
,  ,…,
,…, 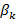 − неотрицательные целые числа, то
− неотрицательные целые числа, то , нок
, нок  ,
,  ,
,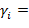 min
min  ,
,  },
},  ,
,  ,
,  ,
,  , …,
, …,  . Отсюда следует, что
. Отсюда следует, что нод
нод 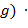 нок
нок 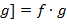 .
. является полем тогда и только тогда, когда
является полем тогда и только тогда, когда  являются классы вычетов
являются классы вычетов  , где
, где 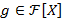 . Классы вычетов
. Классы вычетов  и
и  совпадают тогда и только тогда, когда
совпадают тогда и только тогда, когда  , т.е. и при дении на дают один и тот же остаток. Поэтому различные элементы в
, т.е. и при дении на дают один и тот же остаток. Поэтому различные элементы в  , где
, где  степени <
степени <  . Отметим, что роль нуля и единицы в
. Отметим, что роль нуля и единицы в 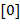 и
и  , где
, где  и
и  − нуль и единица поля
− нуль и единица поля  для некоторых многочленов
для некоторых многочленов  ,
,  . Так как
. Так как  и
и 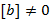 и
и , то
, то  . Пусть
. Пусть 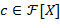 − любой ненулевой многочлен степени
− любой ненулевой многочлен степени  (так что
(так что  − произвольный элемент кольца
− произвольный элемент кольца 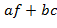 для некоторых
для некоторых  ,
, . Значит,
. Значит, 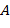 − подкольцо с единицей целостного кольца
− подкольцо с единицей целостного кольца  .
. называется корнем (или нулём) многочлена
называется корнем (или нулём) многочлена  , если
, если  . (Говорят также, что
. (Говорят также, что  − корень уравнения
− корень уравнения  .)
.)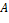 к кольцу
к кольцу 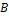 (для которого
(для которого  может не иметь корней в
может не иметь корней в  , многочлен
, многочлен  можно рассматривать как элемент кольца
можно рассматривать как элемент кольца  . При этом
. При этом  не имеет корней в
не имеет корней в 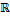 , но имеет два корня в
, но имеет два корня в  (именно:
(именно:  и –
и – 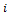 , где
, где  ). Как бы там ни было, мы рассмотрим сначала случай
). Как бы там ни было, мы рассмотрим сначала случай  .
. является корнем многочлена
является корнем многочлена 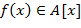 тогда и только тогда, когда
тогда и только тогда, когда 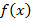 делится на
делится на  .
.
 +
+  , deg
, deg  , то
, то  тогда и только тогда, когда
тогда и только тогда, когда  (или - кратным корнем) многочлена
(или - кратным корнем) многочлена  делится на
делится на 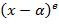 , но не делится на
, но не делится на 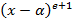 . При
. При 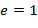 корень
корень  называется простым, а при
называется простым, а при 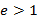 − кратным.
− кратным.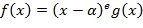 , где
, где 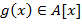 и
и  . Так как
. Так как 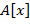 − целостное кольцо, то deg
− целостное кольцо, то deg  .
.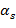 − различные корни ненулевого многочлена
− различные корни ненулевого многочлена 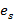 соответственно, то
соответственно, то
 такого, что
такого, что 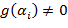 ,
, 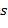 . При этом
. При этом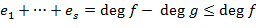 .
. . При
. При  доказывать нечего. Пусть доказано, что
доказывать нечего. Пусть доказано, что
 и многочлена
и многочлена  такого, что
такого, что  ,
,  ,…,
,…, 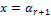 даёт
даёт .
. ,
,  . Пусть
. Пусть  , г
, г  (и, очевидно,
(и, очевидно,  ,
,  ,
, . Допустим, что
. Допустим, что 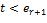 . Тогда, используя закон сокращения в целостном кольце, получаем
. Тогда, используя закон сокращения в целостном кольце, получаем  , что, однако, невозможно ввиду
, что, однако, невозможно ввиду и
и  .
. . Аналогично доказываем, что
. Аналогично доказываем, что  . Поэтому
. Поэтому  и
и ,
, ,
,  . Это и требовалось показать. Наконец, неравенство (2) непосредственно вытекает из (1). ∎
. Это и требовалось показать. Наконец, неравенство (2) непосредственно вытекает из (1). ∎ (
( − кольцо целых чисел по модулю 8), то
− кольцо целых чисел по модулю 8), то  =
= 
 ; разложение
; разложение  также неоднозначно:
также неоднозначно: .
. степени
степени  .
.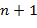 корней, то возникает противоречие с неравенством в (2). Если
корней, то возникает противоречие с неравенством в (2). Если  , то многочлен
, то многочлен  имеет степень
имеет степень  , но не менее
, но не менее 


