
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Число неприводимых многочленов заданной степени над конечным полем.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Обозначим через Теорема.
где Доказательство. Пусть
любой степени
Вычисляя степени многочленов в обеих частях этого равенства, получаем соотношение:
из которого, применяя формулу обращения Мёбиуса, получаем выражение для Из предыдущих результатов следует, что для любого
ЛИТЕРАТУРА
Алексеев В. Б. Теорема Абеля в задачах и решениях. – М.: МЦМНО, 2001. Биркгоф Г., Барти Т. Современная прикладная алгебра. – М.: Мир, 1976. Боревич З. И., Шафаревич И. Р. Теория чисел. – М: Наука, 1972. Бухштаб А. А. Теория чисел. – М: Наука, 1966. Винберг Э. Б. Курс алгебры. – М.: Фактория, 2002. Воеводин В. В. Линейная алгебра. − М.: Наука, 1980. Ван дер Варден Б. Л. Алгебра. – М.: Наука, 1947, 1979. Виноградов И. М. Основы теории чисел. Изд. 7-ое. – М.: Наука, 1965. Глухов М. М., Елизаров В. П., Нечаев А. А. Алгебра. В 2-х т. – М.: Гелиос АРВ, 2003. Горенстейн Д. Конечные простые группы. Введение в их классификацию. – М.: Мир, 1985. Елизаров В. П. Конечныв кольца. – М., 1993; М.: Гелиос АРВ, 2006. Елизаров В. П., Нечаев А. А. Высшая алгебра. Ч. 1, 3. – М., 1976, Ч. 2, 4. – М., 1977. Ильин В. А., Позняк Э. Г. Линейная алгебра. – М.: Наука, 1984. Калужнин Л. А. Введение в общую алгебру. – М.: Наука, 1973. Каргополов М. И., Мерзляков Ю. И. Основы теории групп. – М.: Наука, 1972. Клиффорд А., Престон Г. Алгебраическая теория полугрупп. – М.: Мир, 1972. Кон П. Универсальные алгебры. – М.: Мир, 1968. Кострикин А. И. Введение в алгебру. – М.: Наука, 1977. Кострикин А. И. Введение в алгебру. Ч. 1-3. – М.: Физмат, 2000, 2002. Кострикин А. И., Манин Ю. И. Линейная алгебра и геометрия. – М.: Наука, 1986. Куликов Л. Я. Алгебра и теория чисел. – М: Высшая школа, 1979. Курош А. Г. Курс высшей алгебры. – М.: Наука, 1975. Курош А. Г. Теория групп. – М.: Наука, 1944, 1967(3-е изд.).
Курош А. Г. Лекции по общей алгебре. − М.: Физмат, 1962. Кэртис Ч., Райнер И. Теория представлений конечных групп и ассоциативных алгебр. – М.: Наука, 1969. Ламбек И. Кольца и модули. – М.: Мир, 1971. Ленг С. Алгебра. – М.: Мир, 1968. Лидл Р., Нидеррайтер Г. Конечные поля. – В 2-х томах. – М.: Мир, 1988. Лидл Р., Пильц Г. Прикладная абстрактная алгебра. – Екатеринбург: Изд-во УГУ, 1996. Линдон Р., Шупп П. Комбинаторная теория групп. – М.: Мир, 1980. Ляпин Е. С. Полугруппы. − М.: Физматгиз, 1960. Ляпин Е. С., Евсеев А. Е. Алгебра и теория чисел. Чч. 1-2. – М.: Просвещение, 1974, 1978.
Мальцев А. И. Основы линейной алгебры. – М.: Гостехиздат, 1956. Берлекэмп Э. Алгебраическая теория кодирования. – М.: Мир, 1971. Каргополов М. И., Мерзляков Ю. И. Основы теории групп. – М.: Наука, 1972. Магнус В., Коррас А., Солитэр Д. Комбинатопрная тгория групп. – М: Наука, 1974. Мальцев А. И. Алгебраические системы. − М.: Наука, 1970. Общая алгебра. Справочная математическая библиотека. Т. 1,2. – М: Наука, 1990. Окунев Л. Я. Высшая алгебра. − М.: Просвещение, 1966. Скорняков Л. А. Элементы алгебры. – М: Наука, 1980. Скорняков Л. А. Элементы общей алгебры. – М: Наука, 1983. Ольшанский А. Ю. Геометрия определяющих соотношгний в группах. – М: Наука, 1989. Плоткин Б. И. Группы автоморфизмов алгебраических систем. – М: Наука, 1966. Погорелов Б. А. Основы теории групп подстановок. – М., 1985. Постников М. М. Основы теории Галуа. − М.: Физматгиз, 1960. Прасолов В. Многочлены. − М.: МЦМНО, 1999. Узков А. И. Поля. – М., 1969. Узков А. И. Группы и теория Галуа. – М., 1971. Фаддеев Д. К. Лекции по алгебре. – М: Наука, 1984. Фукс Л. Бесконечные абелевы группы. Тт. 1-2. – М.: Мир, 1974, 1977. Холл Теория групп. – М: ИЛ, 1962. Шафаревич И. Р. Основные понятия алгебры. – М; Ижевск, R&C Dinamics, 2001. ТЕОРИЯ КОДИРОВАНИЯ Кассами Т., Токура Н., Ивадари Е., Инагаки Я. Теория кодирования. – М.: Мир, 1978. Мак-Вильямс Ф. Дж., Слоэн Н. Дж. Теория кодов, исправляющих ошибки. – М.: Связь, 1979. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. – М.: Мир, 1976.
|
|||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 642; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.195.78 (0.008 с.) |

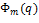 число унитарных неприводимых многочленов степени
число унитарных неприводимых многочленов степени  над полем
над полем  .
.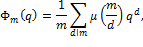
 − функция Мёбиуса.
− функция Мёбиуса. − один из унитарных неприводимых многочленов степени
− один из унитарных неприводимых многочленов степени  над
над 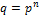 . Его поле разложения изоморфно факторкольцу
. Его поле разложения изоморфно факторкольцу  . Если
. Если  и
и 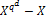 имеют общий корень, то
имеют общий корень, то  , если
, если  . Так как многочлен
. Так как многочлен 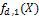 ,
, 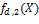 , …,
, …, 
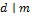 , причём ровно по одному разу. Поэтому
, причём ровно по одному разу. Поэтому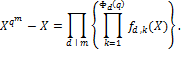

 . ∎
. ∎



