Симметрическая и знакопеременная группы
Пусть  − множество из − множество из  элементов. Природа элементов множества элементов. Природа элементов множества  несущественна; поэтому удобно считать, что несущественна; поэтому удобно считать, что  , ,  , …, , …,  . Совокупность всех биективных (т.е. взаимно однозначных) отображений . Совокупность всех биективных (т.е. взаимно однозначных) отображений  множества множества  на себя с операцией композиции отображений образует группу; её называют симметрической группой степени на себя с операцией композиции отображений образует группу; её называют симметрической группой степени  (или на (или на  точках) и обозначают через точках) и обозначают через  , но чаще всего как , но чаще всего как  . Произвольный элемент . Произвольный элемент  называют подстановкой, или пе рестановкой на множестве называют подстановкой, или пе рестановкой на множестве  . .
Замечание. Термины ″подстановка″ и ″перестановка″ будут считаться синонимами, хотя следует отметить определённое различие между ними: подстановка − это замена одного объекта другим, а перестановка − это перемещение объекта с одного места на другое. Далее, для определённости, будем пользоваться термином перестановка.
В наглядной форме перестановку  , ,  записывают в виде двустрочной таблицы записывают в виде двустрочной таблицы
(1) 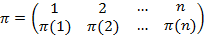 , ,
где нижняя строка содержит те же элементы, что и верхняя, но, возможно, в другом порядке. Поскольку верхняя строка таблицы стандартна, то перестановка записывается в виде слова  . Перестановка . Перестановка
  , ,
соответствующая тождественному отображению, называется единичной, или тождественной.
Произведение (умножение)  перестановок перестановок  и σ определяется в соответствии с общим правилом композиции отображений: и σ определяется в соответствии с общим правилом композиции отображений:
 , ,  . .
Таблица для перестановки  , обратной по отношению к перестановке , обратной по отношению к перестановке  , получается из таблицы , получается из таблицы 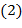 обычной перестановкой строк с последующим упорядочением столбцов так, чтобы верхняя строка получила стандартный вид: обычной перестановкой строк с последующим упорядочением столбцов так, чтобы верхняя строка получила стандартный вид:  , ,  ,…, ,…,  . Напомним, что . Напомним, что  . .
Пример. Пусть  , ,  Тогда Тогда  , ,  , ,
 , ,  . .
Другой общепринятый способ представления перестановки на множестве  − это разложение её на независимые циклы вида − это разложение её на независимые циклы вида
 , ,  , ,
где  , а , а  − наименьшее число, для которого − наименьшее число, для которого  , ,  Такому циклу соответствует перестановка Такому циклу соответствует перестановка
 , ,
которую будем обозначать как
 , ,  , ,  ,…, ,…, 
и называть простым циклом длины  . Эта перестановка оставляет на месте элементы множества . Эта перестановка оставляет на месте элементы множества  , где , где
 , ,  , ,  , …, , …,  , ,
т.е.  , если , если  , и перемещает элемент , и перемещает элемент  в в  , т.е. , т.е.  , если , если  . .
Всякая перестановка  может быть разложена в произведение может быть разложена в произведение

простых циклов  , ,  , …, , …,  . Такое разложение однозначно, если не принимать во внимание порядок сомножителей, поскольку простые циклы перестановочны: . Такое разложение однозначно, если не принимать во внимание порядок сомножителей, поскольку простые циклы перестановочны:  , ,  . Циклы длины . Циклы длины  называются тривиальными. Поскольку им соответствуют неподвижные точки множества называются тривиальными. Поскольку им соответствуют неподвижные точки множества  , то их при записи разложения обычно опускают. , то их при записи разложения обычно опускают.
Пример. Перестановка

разлагается в произведение циклов длины  , ,  и и  : :  . .
Циклы длины  называются транспозициями. Транспозиция называются транспозициями. Транспозиция  , ,  меняет местами элементы меняет местами элементы  и и  , оставляя остальные элементы неподвижными. Очевидно, что , оставляя остальные элементы неподвижными. Очевидно, что  и и  (заметим, что преобразования с таким свойством называют инволютивными). (заметим, что преобразования с таким свойством называют инволютивными).
Теорема. Всякая перестановка разлагается в произведение транспозиций.
Доказательство. Имеем
 . .
Аналогично и любой другой цикл представим в виде произведения транспозиций. Отсюда следует, что и произведение простых циклов, в которое разлагается любая перестановка, можно представить в виде произведения транспозиций. ∎
Замечание. Транспозиции, вообще говоря, не коммутируют. Например,
 , но , но  . Разложение перестановки в произведение транспозиций в общем случае неоднозначно. . Разложение перестановки в произведение транспозиций в общем случае неоднозначно.
Пусть  − любая перестановка, − любая перестановка,  ,…, ,…,  − любая функция от − любая функция от  переменных. переменных.
Положим
( ,…, ,…,  ,…, ,…,  . .
Говорят, что функция  получена действием получена действием  на на  . .
Пример. Пусть  , ,  ,…, ,…,  . Тогда . Тогда 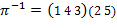 и и  ,…, ,…,  . . 
Функция  ,…, ,…,  называется кососимметрической, если называется кососимметрической, если  для любой транспозиции для любой транспозиции  на множестве на множестве  , т.е. , т.е.
 , ,  ,…, ,…,  , ,  , ,  ,…, ,…,  , ,  для любых для любых   . .
Пример кососимметрической функции. Определитель Вандермонда
 ,…, ,…, 
при перестановке столбцов меняет знак. Значит,  − кососимметрическая функция. − кососимметрическая функция.
Лемма. Пусть  , ,  − любые перестановки, − любые перестановки,  ,…, ,…,  − любая функция. Тогда − любая функция. Тогда
 . .
Доказательство:
(( ) ∘ ) ∘  ,…, ,…,  ,…, ,…, 
 ,…, ,…,  ,…, ,…, 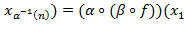 ,…, ,…,  ∎ ∎
Теорема. Пусть  − любая перестановка, а − любая перестановка, а
 
− любое разложение перестановки  в произведение транспозиций. Тогда число в произведение транспозиций. Тогда число

полностью определяется перестановкой  и не зависит от способа её разложения. и не зависит от способа её разложения.
Число  , называемое сигнатурой (или чётностью) перестановки , называемое сигнатурой (или чётностью) перестановки  , удовлетворяет свойству: , удовлетворяет свойству:
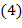  для всех для всех  , ,  . .
Доказательство. Пусть  ,…, ,…,  − любая кососимметрическая функция, не равная тождественно нулю. Например, − любая кососимметрическая функция, не равная тождественно нулю. Например,  ,…, ,…,  Согласно лемме Согласно лемме

Поскольку левая часть этого соотношения зависит от  , но не зависит от её разложения в произведение транспозиций, то немедленно получаем требуемое утверждение. Кроме того, , но не зависит от её разложения в произведение транспозиций, то немедленно получаем требуемое утверждение. Кроме того,
 , ,
что доказывает (9). ∎
Перестановка  называется чётной, если называется чётной, если  , и нечётной, если , и нечётной, если  . .
Любая транспозиция − нечётная перестановка.
Теорема. Если перестановка  разлагается в произведение простых циклов разлагается в произведение простых циклов  , …, , …,  , с длинами , с длинами  ,…, ,…,  , то , то  , где , где

Доказательство. Так как простой цикл  , имеющий длину , имеющий длину  , разлагается в произведение , разлагается в произведение  транспозиций, то транспозиций, то  . Остаётся учесть, что . Остаётся учесть, что  . ∎ . ∎
Теорема. 
Доказательство. Нижнюю строку в 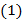 можно выбрать можно выбрать  способами .∎ способами .∎
Теорема. Чётные перестановки в  образуют подгруппу порядка образуют подгруппу порядка  . (Эту подгруппу называют знакопеременной группой степени . (Эту подгруппу называют знакопеременной группой степени  и обозначают через и обозначают через  .) .)
Доказательство. Имеем
 , ,  ∈ ∈  ; ;
 − единица в − единица в  ; ;
 ). ).
Другими словами, для  все аксиомы группы выполняются. Вычислим её порядок. все аксиомы группы выполняются. Вычислим её порядок.
Представим  в виде объединения в виде объединения  , где , где  − множество нечётных перестановок. Рассмотрим отображение − множество нечётных перестановок. Рассмотрим отображение  , определяемое правилом , определяемое правилом  , где , где  − транспозиция − транспозиция   . Поскольку . Поскольку  , то , то  . Следовательно, отображение . Следовательно, отображение  инъективно и, ввиду конечности инъективно и, ввиду конечности  , биективно. Оно переводит чётные перестановки в нечётные, а нечётные − в чётные. Значит, , биективно. Оно переводит чётные перестановки в нечётные, а нечётные − в чётные. Значит,  . ∎ . ∎
Морфизмы групп. Пусть ( , ∘, , ∘,  ), ( ), ( , ∗, , ∗,  ) − группы. ) − группы.
Определение. Отображение   → →  группы группы  в группу в группу  называется гомоморфизмом, если называется гомоморфизмом, если
(1)  , ∀ , ∀  , ,  . .
Отметим простейшие свойства гомоморфизмов:
1) Единица отображается в единицу. Действительно,  , ∀ , ∀  . Значит, . Значит,  , откуда следует, что , откуда следует, что 
2)  Имеем Имеем



Ядром гомоморфизма f называется множество
 . .
Утверждение. 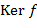 − подгруппа в − подгруппа в  . .
Доказательство. Имеем:
 , ,  ; ;
 ; ;
 . .
Другими словами, для  , ,  выполняются все аксиомы группы. ∎ выполняются все аксиомы группы. ∎
Аналогично доказывается следующее
Утверждение.  − подгруппа в − подгруппа в  . .
Далее будем опускать знаки  и и  . .
Определение. Взаимно однозначный (биективный) гомоморфизм  называется изоморфизмом. называется изоморфизмом.
Утверждение. Если  − изоморфизм, то существует обратное отображение − изоморфизм, то существует обратное отображение  , также являющееся изоморфизмом. , также являющееся изоморфизмом.
Доказательство. Так как  −биекция, то обратное отображение −биекция, то обратное отображение  заведомо существует. Поэтому достаточно убедиться в выполнении свойства заведомо существует. Поэтому достаточно убедиться в выполнении свойства  . Ввиду биективности . Ввиду биективности  для любых для любых 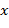 , ,  найдутся такие найдутся такие  , ,  , что , что  , ,  и и  , ,  . Но тогда . Но тогда  ∎ ∎
Группы G и H называются изоморфными (обозначение:  ), если существуют изоморфизмы, переводящие одну группу в другую. Изоморфные группы имеют одинаковые алгебраические свойства (если не рассматривать какие-либо дополнительно определённые на них структуры). В абстрактной теории групп к ним относятся как к одинаковым объектам. ), если существуют изоморфизмы, переводящие одну группу в другую. Изоморфные группы имеют одинаковые алгебраические свойства (если не рассматривать какие-либо дополнительно определённые на них структуры). В абстрактной теории групп к ним относятся как к одинаковым объектам.
Замечание. В определении гомоморфизма от отображения  не требуется не только биективности, но и сюръективности. Однако последнее не очень-то существенно. Поскольку Im не требуется не только биективности, но и сюръективности. Однако последнее не очень-то существенно. Поскольку Im  − подгруппа в − подгруппа в  , можно вместо отображения , можно вместо отображения  рассматривать отображение 𝜑: рассматривать отображение 𝜑:  , которое уже будет сюръективным. Главное же отличие гомоморфизма от изоморфизма заключается в наличии нетривиального ядра , которое уже будет сюръективным. Главное же отличие гомоморфизма от изоморфизма заключается в наличии нетривиального ядра 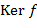 , являющегося мерой неинъективности. , являющегося мерой неинъективности.
Утверждение. Сюръективный гомоморфизм  является изоморфизмом тогда и только тогда, когда ядро отображения является изоморфизмом тогда и только тогда, когда ядро отображения  тривиально, т.е. тривиально, т.е.  }. }.
Доказательство. Если ядро 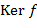 нетривиально, то отображение нетривиально, то отображение  не является инъекцией, следовательно, не является изоморфизмом. Теперь предположим, что ядро тривиально, т.е. состоит из одного элемента не является инъекцией, следовательно, не является изоморфизмом. Теперь предположим, что ядро тривиально, т.е. состоит из одного элемента  . Допустим, что . Допустим, что  для некоторых для некоторых  , ,  ∈ ∈  . Тогда . Тогда
 . .
Другими словами, если  , то , то  . Значит, . Значит,  − инъективное отображение и, следовательно, изоморфизм. ∎ − инъективное отображение и, следовательно, изоморфизм. ∎
Теорема Кэли. Любая конечная группа G порядка  изоморфна некоторой подгруппе симметрической группы изоморфна некоторой подгруппе симметрической группы  . .
Доказательство. Пусть 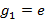 , ,  ,…, ,…,  − все элементы группы − все элементы группы  . Для произвольного . Для произвольного  рассмотрим отображение рассмотрим отображение  , определяемое формулой , определяемое формулой
 . .
Так как  , то , то  . Поэтому . Поэтому  − биекция на − биекция на  , и, следовательно, , и, следовательно,

− подстановка на  точках точках  , ,  ,…, ,…,  . Положим теперь . Положим теперь
 } }
и покажем, что множество  образует группу относительно композиции(произведения) отображений, определяемых, как обычно, по правилу образует группу относительно композиции(произведения) отображений, определяемых, как обычно, по правилу  Для этого проверим выполнимость аксиом Для этого проверим выполнимость аксиом  : :
 . Поскольку . Поскольку  , то , то
  . .
Другими словами, множество  замкнуто относительно операции замкнуто относительно операции  . .
 . Как любая композиция отображений, операция ассоциативна: . Как любая композиция отображений, операция ассоциативна:
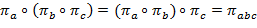 . .
 . Подстановка . Подстановка  − нейтральный элемент (единица) в − нейтральный элемент (единица) в  . .
 . Так как . Так как  , то , то  , т.е. каждый элемент в , т.е. каждый элемент в  имеет обратный. имеет обратный.
Таким образом,  − группа. Изоморфизм групп − группа. Изоморфизм групп  и и  устанавливается соответствием устанавливается соответствием
 , которое биективно и удовлетворяет, согласно (2), свойству сохранения операции: , которое биективно и удовлетворяет, согласно (2), свойству сохранения операции:  . ∎ . ∎
Замечание. Теорема Кэли имеет важное значение в теории групп. Она выделяет универсальный объект − семейство симметрических групп  , ,  , ,  , ,  ,…, как хранилище всех конечных групп, рассматриваемых с точностью до изоморфизма. ,…, как хранилище всех конечных групп, рассматриваемых с точностью до изоморфизма.
Другие морфизмы. Гомоморфизм, являющийся отображением на, называется сюръективным, или эпиморфизмом. Гомоморфизм 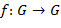 группы группы  в себя называется эндоморфизмом. Изоморфизм группы на себя называется автоморфизмом. Множество всех эндоморфизмов образует полугруппу, а множество всех автоморфизмов − группу. в себя называется эндоморфизмом. Изоморфизм группы на себя называется автоморфизмом. Множество всех эндоморфизмов образует полугруппу, а множество всех автоморфизмов − группу.
Смежные классы. Пусть  − группа, а − группа, а  − её подгруппа. Левый смежный класс группы G по подгруппе H определяется как множество − её подгруппа. Левый смежный класс группы G по подгруппе H определяется как множество
 , ,  . .
Всякий элемент из  называется представителем смежного класса. Отображение называется представителем смежного класса. Отображение
 : :  является биекцией H на является биекцией H на  . Поэтому любые два смежных класса . Поэтому любые два смежных класса  и и  равномощны. равномощны.
Смежные классы  и и  , имеющие хотя бы один общий элемент совпадают. Действительно, пусть , имеющие хотя бы один общий элемент совпадают. Действительно, пусть   , где , где  , ,  ∈ ∈  . Тогда . Тогда   , ,   . Так как h ∈ . Так как h ∈  и и  = =  , то , то  H H  . .
Таким образом, G есть объединение непересекающихся левых смежных классов:
 . .
Аналогичные замечания справедливы и для правых смежных классов
 , ,  ∈ G. ∈ G.
Число левых смежных классов группы G обозначается через (G:  ) и называется индексом подгруппы H в G. Индекс тривиальной подгруппы H ) и называется индексом подгруппы H в G. Индекс тривиальной подгруппы H  } равен порядку группы G. } равен порядку группы G.
Очевидно, что
(G:  | | 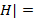 | | 
В частности, имеет место
Теорема Лагранжа. Порядок конечной группы делится без остатка на порядок любой её подгруппы.
Следствие. Если порядок группы G равен простому числу, то G не имеет собственных подгрупп, т.е. отличных от самой группы G и тривиальной подгруппы 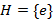 порядка порядка 
Упражнения.
Замечание. Теорема Лагранжа, вообще говоря, не допускает обращения: если m делит порядок | 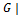 , то это ещё не означает, что в группе , то это ещё не означает, что в группе  существует подгруппа порядка m. Например, в знакопеременной группе существует подгруппа порядка m. Например, в знакопеременной группе  нет подгрупп порядка 6. (Проверить самостоятельно.) Однако для абелевых групп обращение теоремы Лагранжа имеет место. Кроме того, если m = нет подгрупп порядка 6. (Проверить самостоятельно.) Однако для абелевых групп обращение теоремы Лагранжа имеет место. Кроме того, если m =  степень простого числа, то в группе степень простого числа, то в группе  существует подгруппа порядка m (см. теорему Силова). существует подгруппа порядка m (см. теорему Силова).
Множество левых смежных классов обозначается через G ∕  (или же через (или же через  , если есть необходимость отличать его от множества правых смежных классов , если есть необходимость отличать его от множества правых смежных классов  ). Очевидно, что для абелевых групп ). Очевидно, что для абелевых групп  , но в общем случае множество левых смежных классов может не совпадать с множеством правых смежных классов. , но в общем случае множество левых смежных классов может не совпадать с множеством правых смежных классов.
Примеры. 1) Пусть  , ,  , ,  , ,  , ,  . Поскольку . Поскольку  и и  − абелевы группы, то множества левых и правых смежных классов совпадают. Имеем следующее разложение на − абелевы группы, то множества левых и правых смежных классов совпадают. Имеем следующее разложение на  смежные классы: смежные классы:
 , ,
где
 , ,  , , 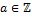 . .
2) Пусть  , ,  = =  (12)>. Разложения группы (12)>. Разложения группы  по подгруппе по подгруппе  в левые в левые  и правые смежные и правые смежные  классы имеют вид: классы имеют вид: 
 , ,
где
 , ,  , ,  ; ;
 , ,  , , 
Нормальные делители. В группах особенно важную роль играют те подгруппы, относительно которых левые и правые смежные классы совпадают. Такие подгруппы называют нормальными.
Определение. Подгруппа  называется нормальной или нормальным делителем группы называется нормальной или нормальным делителем группы  , что обозначается , что обозначается  , если , если
 для любого для любого  , ,
т.е. каждый левый смежный класс  совпадает с правым смежным классом совпадает с правым смежным классом  . .
Если  – собственная подгруппа в – собственная подгруппа в  , то пишем , то пишем  . .
Лемма. Любое из следующих условий на подгруппу  группы группы  равносильно её нормальности: равносильно её нормальности:
(1)  для любого для любого  . .
(2)  для любых для любых  , ,  ; ;
Доказательство. (1)  . (2) . (2) 
  . ∎ . ∎
В абелевых группах, в силу коммутативности групповой операции, любая подгруппа является нормальным делителем.
Группа  называется простой, если в ней нет неединичных собственных нормальных подгрупп. Примером таких групп являются группы простого порядка называется простой, если в ней нет неединичных собственных нормальных подгрупп. Примером таких групп являются группы простого порядка 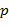 , поскольку в них, как следует из теоремы Лагранжа, нет неединичных собственных подгрупп. , поскольку в них, как следует из теоремы Лагранжа, нет неединичных собственных подгрупп.
В неабелевых группах могут быть подгруппы как являющиеся, так и не являющиеся нормальными делителями.
Пример. Пусть  . 1) . 1)  , ,  , ,  . Левыми смежными классами группы . Левыми смежными классами группы 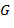 по по  являются: являются:  и и  , ,  , ,  , где , где  . Такие же и правые классы. Значит, . Такие же и правые классы. Значит,  − нормальный делитель в − нормальный делитель в  . 2) Пусть теперь . 2) Пусть теперь  { {  , (12)}. Рассмотрим разложение , (12)}. Рассмотрим разложение  в левые и правые смежные классы по подгруппе в левые и правые смежные классы по подгруппе  : :
 , (12)}∪{(13), , (12)}∪{(13),  , ,  }; };
 , , 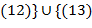 , ,  , ,  . .
Множества смежных классов  и и  не совпадают. Значит, не совпадают. Значит,  не является нормальной подгруппой в не является нормальной подгруппой в  . (Замечание: термин ″ ненормальная подгруппа ″ рекомендуется не употреблять!) . (Замечание: термин ″ ненормальная подгруппа ″ рекомендуется не употреблять!)
Важным свойством нормальной подгруппы является тот факт, что множество левых (равно, как и правых) смежных классов по ней можно наделить групповой структурой.
Теорема. Пусть   − нормальная подгруппа. Множество всех различных левых смежных классов − нормальная подгруппа. Множество всех различных левых смежных классов  | |  с операцией умножения с операцией умножения

образует группу  ∕ ∕  , которая называется факторгруппой группы , которая называется факторгруппой группы  по нормальной подгруппе по нормальной подгруппе  . .
Доказательство. Вначале докажем, что операция ∘ определена корректно, т.е. не зависит от выбора представителей смежных классов.Требуется показать, что
 , ,  . .
Напомним, что  | 


 − множество из
− множество из  элементов. Природа элементов множества
элементов. Природа элементов множества  ,
,  , …,
, …,  . Совокупность всех биективных (т.е. взаимно однозначных) отображений
. Совокупность всех биективных (т.е. взаимно однозначных) отображений  множества
множества  , но чаще всего как
, но чаще всего как  . Произвольный элемент
. Произвольный элемент  называют подстановкой, или пе рестановкой на множестве
называют подстановкой, или пе рестановкой на множестве  ,
,  записывают в виде двустрочной таблицы
записывают в виде двустрочной таблицы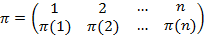 ,
, . Перестановка
. Перестановка
 ,
, перестановок
перестановок  и σ определяется в соответствии с общим правилом композиции отображений:
и σ определяется в соответствии с общим правилом композиции отображений: ,
,  , обратной по отношению к перестановке
, обратной по отношению к перестановке  , получается из таблицы
, получается из таблицы 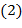 обычной перестановкой строк с последующим упорядочением столбцов так, чтобы верхняя строка получила стандартный вид:
обычной перестановкой строк с последующим упорядочением столбцов так, чтобы верхняя строка получила стандартный вид:  ,
,  .
. ,
,  Тогда
Тогда  ,
,  ,
, ,
,  .
. ,
,  ,
, , а
, а  − наименьшее число, для которого
− наименьшее число, для которого  ,
,  Такому циклу соответствует перестановка
Такому циклу соответствует перестановка ,
, ,
,  ,
,  ,…,
,…, 
 . Эта перестановка оставляет на месте элементы множества
. Эта перестановка оставляет на месте элементы множества  , где
, где ,
,  ,
, , если
, если  , и перемещает элемент
, и перемещает элемент  в
в  , т.е.
, т.е.  , если
, если  .
.
 ,
,  , …,
, …,  . Такое разложение однозначно, если не принимать во внимание порядок сомножителей, поскольку простые циклы перестановочны:
. Такое разложение однозначно, если не принимать во внимание порядок сомножителей, поскольку простые циклы перестановочны:  ,
,  . Циклы длины
. Циклы длины 
 и
и  :
:  .
. называются транспозициями. Транспозиция
называются транспозициями. Транспозиция  ,
,  меняет местами элементы
меняет местами элементы  и
и  и
и  (заметим, что преобразования с таким свойством называют инволютивными).
(заметим, что преобразования с таким свойством называют инволютивными). .
. , но
, но  . Разложение перестановки в произведение транспозиций в общем случае неоднозначно.
. Разложение перестановки в произведение транспозиций в общем случае неоднозначно. ,…,
,…,  − любая функция от
− любая функция от  ,…,
,…,  ,…,
,…,  .
. получена действием
получена действием  .
. ,
,  . Тогда
. Тогда 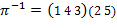 и
и  ,…,
,…,  .
. 
 называется кососимметрической, если
называется кососимметрической, если  для любой транспозиции
для любой транспозиции  на множестве
на множестве  ,
,  ,…,
,…,  ,
,  ,
,  для любых
для любых 

 ,
,  − любые перестановки,
− любые перестановки,  .
. ) ∘
) ∘  ,…,
,…,  ,…,
,…, 
 ,…,
,…,  ,…,
,…, 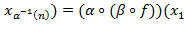 ,…,
,…,  ∎
∎


 , называемое сигнатурой (или чётностью) перестановки
, называемое сигнатурой (или чётностью) перестановки 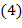
 для всех
для всех  Согласно лемме
Согласно лемме
 ,
, , и нечётной, если
, и нечётной, если  .
. ,…,
,…,  , то
, то  , где
, где
 , имеющий длину
, имеющий длину  , разлагается в произведение
, разлагается в произведение  транспозиций, то
транспозиций, то  . Остаётся учесть, что
. Остаётся учесть, что  . ∎
. ∎
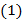 можно выбрать
можно выбрать  способами .∎
способами .∎ . (Эту подгруппу называют знакопеременной группой степени
. (Эту подгруппу называют знакопеременной группой степени  .)
.) ∈
∈  ;
; − единица в
− единица в  ).
). , где
, где  − множество нечётных перестановок. Рассмотрим отображение
− множество нечётных перестановок. Рассмотрим отображение  , определяемое правилом
, определяемое правилом  , где
, где 
 . Поскольку
. Поскольку  , то
, то  . Следовательно, отображение
. Следовательно, отображение  . ∎
. ∎ , ∘,
, ∘,  ), (
), ( , ∗,
, ∗,  ) − группы.
) − группы.
 группы
группы  в группу
в группу  , ∀
, ∀  ,
,  .
. , ∀
, ∀  . Значит,
. Значит,  , откуда следует, что
, откуда следует, что 
 Имеем
Имеем


 .
.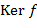 − подгруппа в
− подгруппа в  .
. ;
; ;
; .
. ,
,  выполняются все аксиомы группы. ∎
выполняются все аксиомы группы. ∎ − подгруппа в
− подгруппа в  и
и  .
. называется изоморфизмом.
называется изоморфизмом. , также являющееся изоморфизмом.
, также являющееся изоморфизмом. заведомо существует. Поэтому достаточно убедиться в выполнении свойства
заведомо существует. Поэтому достаточно убедиться в выполнении свойства  . Ввиду биективности
. Ввиду биективности 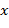 ,
,  найдутся такие
найдутся такие  ,
,  и
и  ,
,  . Но тогда
. Но тогда  ∎
∎ ), если существуют изоморфизмы, переводящие одну группу в другую. Изоморфные группы имеют одинаковые алгебраические свойства (если не рассматривать какие-либо дополнительно определённые на них структуры). В абстрактной теории групп к ним относятся как к одинаковым объектам.
), если существуют изоморфизмы, переводящие одну группу в другую. Изоморфные группы имеют одинаковые алгебраические свойства (если не рассматривать какие-либо дополнительно определённые на них структуры). В абстрактной теории групп к ним относятся как к одинаковым объектам. , которое уже будет сюръективным. Главное же отличие гомоморфизма от изоморфизма заключается в наличии нетривиального ядра
, которое уже будет сюръективным. Главное же отличие гомоморфизма от изоморфизма заключается в наличии нетривиального ядра  }.
}. . Допустим, что
. Допустим, что  для некоторых
для некоторых  ∈
∈  .
. , то
, то  . Значит,
. Значит, 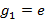 ,
,  ,…,
,…,  − все элементы группы
− все элементы группы  . Для произвольного
. Для произвольного  рассмотрим отображение
рассмотрим отображение  , определяемое формулой
, определяемое формулой .
. , то
, то  . Поэтому
. Поэтому  − биекция на
− биекция на 
 ,
,  }
} образует группу относительно композиции(произведения) отображений, определяемых, как обычно, по правилу
образует группу относительно композиции(произведения) отображений, определяемых, как обычно, по правилу  Для этого проверим выполнимость аксиом
Для этого проверим выполнимость аксиом  :
: . Поскольку
. Поскольку  , то
, то .
. . Как любая композиция отображений, операция ассоциативна:
. Как любая композиция отображений, операция ассоциативна: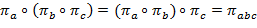 .
. . Подстановка
. Подстановка  − нейтральный элемент (единица) в
− нейтральный элемент (единица) в  . Так как
. Так как  , то
, то  , т.е. каждый элемент в
, т.е. каждый элемент в  , которое биективно и удовлетворяет, согласно (2), свойству сохранения операции:
, которое биективно и удовлетворяет, согласно (2), свойству сохранения операции:  . ∎
. ∎ ,
, 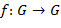 группы
группы  − её подгруппа. Левый смежный класс группы G по подгруппе H определяется как множество
− её подгруппа. Левый смежный класс группы G по подгруппе H определяется как множество ,
,  .
. называется представителем смежного класса. Отображение
называется представителем смежного класса. Отображение является биекцией H на
является биекцией H на  и
и  равномощны.
равномощны.
 , где
, где  ,
,  ∈
∈ 
 ,
, 
 . Так как h ∈
. Так как h ∈  =
=  .
. .
. ,
,  ∈ G.
∈ G. ) и называется индексом подгруппы H в G. Индекс тривиальной подгруппы H
) и называется индексом подгруппы H в G. Индекс тривиальной подгруппы H  } равен порядку группы G.
} равен порядку группы G. |
| 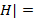 |
| 
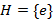 порядка
порядка 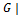 , то это ещё не означает, что в группе
, то это ещё не означает, что в группе  существует подгруппа порядка m. Например, в знакопеременной группе
существует подгруппа порядка m. Например, в знакопеременной группе  нет подгрупп порядка 6. (Проверить самостоятельно.) Однако для абелевых групп обращение теоремы Лагранжа имеет место. Кроме того, если m =
нет подгрупп порядка 6. (Проверить самостоятельно.) Однако для абелевых групп обращение теоремы Лагранжа имеет место. Кроме того, если m =  степень простого числа, то в группе
степень простого числа, то в группе  (или же через
(или же через  , если есть необходимость отличать его от множества правых смежных классов
, если есть необходимость отличать его от множества правых смежных классов  ). Очевидно, что для абелевых групп
). Очевидно, что для абелевых групп  , но в общем случае множество левых смежных классов может не совпадать с множеством правых смежных классов.
, но в общем случае множество левых смежных классов может не совпадать с множеством правых смежных классов. ,
,  ,
,  ,
,  . Поскольку
. Поскольку  − абелевы группы, то множества левых и правых смежных классов совпадают. Имеем следующее разложение на
− абелевы группы, то множества левых и правых смежных классов совпадают. Имеем следующее разложение на  ,
, ,
,  ,
, 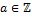 .
. ,
,  =
=  (12)>. Разложения группы
(12)>. Разложения группы  и правые смежные
и правые смежные  классы имеют вид:
классы имеют вид: 
 ,
, ,
,  ,
,  ;
; ,
,  ,
, 
 называется нормальной или нормальным делителем группы
называется нормальной или нормальным делителем группы  , если
, если для любого
для любого  .
. .
. для любого
для любого  для любых
для любых  ,
,  . (2)
. (2) 

 . ∎
. ∎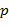 , поскольку в них, как следует из теоремы Лагранжа, нет неединичных собственных подгрупп.
, поскольку в них, как следует из теоремы Лагранжа, нет неединичных собственных подгрупп. . 1)
. 1)  ,
,  ,
,  . Левыми смежными классами группы
. Левыми смежными классами группы 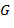 по
по  и
и  ,
,  ,
,  , где
, где  . Такие же и правые классы. Значит,
. Такие же и правые классы. Значит,  − нормальный делитель в
− нормальный делитель в  . 2) Пусть теперь
. 2) Пусть теперь  {
{  , (12)}. Рассмотрим разложение
, (12)}. Рассмотрим разложение  :
: , (12)}∪{(13),
, (12)}∪{(13),  ,
,  };
};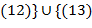 ,
,  ,
,  .
. и
и  не совпадают. Значит,
не совпадают. Значит,  не является нормальной подгруппой в
не является нормальной подгруппой в 
 |
|  с операцией умножения
с операцией умножения
 ,
,  .
.


