
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Замечание о главных идеалах.Содержание книги
Поиск на нашем сайте
Утверждение. В коммутативном кольце Доказательство. Если Следствие. Коммутативное кольцо Доказательство. Любое поле содержит два идеала: нулевое (0) и единичное (1).Других (т.е. собственных) идеалов в поле нет. Если Замечание. Следующий контрпример показывает, что как конечное, так и бесконечное некоммутативное кольцо, содержащее необратимый элемент, может не иметь собственных идеалов. Рассмотрим кольцо
Пусть
Таким образом,
Морфизмы колец. Определение. Пусть
для любых Далее вместо ″кольцевой гомоморфизм″ будем говорить также ″гомоморфизм колец″ или просто ″гомоморфизм″, если ясно, что речь идёт о кольцах. Ядром кольцевого гомоморфизма
где Теорема. Ядро кольцевого гомоморфизма Доказательство. Пусть
Очевидно, что Теорема. Пусть Доказательство. Поскольку
т.е. В дополнение к теореме отметим, что Гомоморфизм мономорфизмом, или инъективным гомоморфизмом, если эпиморфизмом, или сюръективным гомоморфизмом, если образ отображения изоморфизмом, или биективным гомоморфизмом, если Утверждение. Если Доказательство этого утверждения нетрудно осуществить по аналогии с доказательством соответствующего утверждения об изоморфизмах групп. ∎ Ясно, что инъективный кольцевой гомоморфизм
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 258; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.248.150 (0.005 с.) |

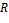 с единицей множество
с единицей множество  всех кратных
всех кратных  любого фиксированного элемента
любого фиксированного элемента  является идеалом в
является идеалом в  и
и 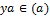 , то
, то 
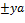 = (
= ( )
) 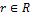 имеем
имеем 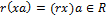 и
и 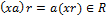 . ∎
. ∎ , среди кратных которого нет единицы. Поэтому
, среди кратных которого нет единицы. Поэтому  является собственным идеалом в
является собственным идеалом в 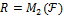 матриц
матриц  второго порядка над произвольным полем ℱ. Пусть в этом кольце
второго порядка над произвольным полем ℱ. Пусть в этом кольце  означает матрицу, у которой
означает матрицу, у которой 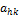 =1, а на остальных местах нули. Другими словами,
=1, а на остальных местах нули. Другими словами, ,
,  ,
,  ,
, 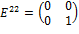 .
.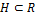 − ненулевой идеал в
− ненулевой идеал в  − матрица из этого идеала с ненулевым элементом
− матрица из этого идеала с ненулевым элементом 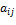 . Тогда идеал должен содержать все матрицы вида
. Тогда идеал должен содержать все матрицы вида 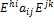 =
= 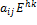 . Выберем любую матрицу
. Выберем любую матрицу 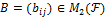 . Так как
. Так как 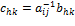 , а затем, обозначив через
, а затем, обозначив через  матрицу с элементами
матрицу с элементами  на главной диагонали и нулями вне её, мы можем представить
на главной диагонали и нулями вне её, мы можем представить 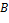 в виде
в виде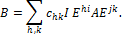
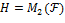 . Отсюда следует, матричное кольцо не имеет собственных идеалов, причем конечно или бесконечно в зависимости от того, конечно или бесконечно
. Отсюда следует, матричное кольцо не имеет собственных идеалов, причем конечно или бесконечно в зависимости от того, конечно или бесконечно  .∎
.∎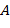 ,
,  кольца. Отображение
кольца. Отображение 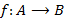 называется кольцевым гомоморфизмом, если оно сохраняет обе операции, т.е.
называется кольцевым гомоморфизмом, если оно сохраняет обе операции, т.е.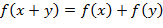 ;
;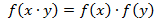
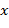 ,
, 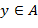 . (Знаки
. (Знаки  и
и  в левой и правой частях этих равенств имеют разный смысл: слева это операции в кольце
в левой и правой частях этих равенств имеют разный смысл: слева это операции в кольце  .)
.)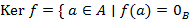 },
},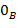 − нуль в кольце
− нуль в кольце 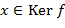 ,
, 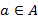 . Тогда
. Тогда ,
, 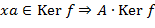 ,
,  .
.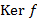 − подкольцо в
− подкольцо в 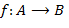 − гомоморфизм колец. Тогда образ
− гомоморфизм колец. Тогда образ 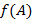 отображения
отображения 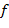 − подкольцо в
− подкольцо в 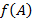 − аддитивная абелева группа (подгруппа группы
− аддитивная абелева группа (подгруппа группы 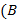 ,
,  ). Пусть
). Пусть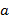 ,
,  , а
, а 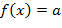 ,
,  Тогда
Тогда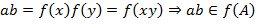 ,
,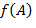 − подкольцо в
− подкольцо в 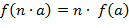 для любых
для любых 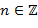 ,
,  служит единицей кольца
служит единицей кольца 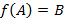 .
.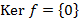 (в этом случае
(в этом случае 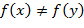 , если
, если 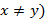 ;
;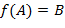 (в этом случае
(в этом случае 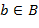 существует
существует 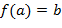 );
);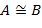 .
. также является изоморфизмом колец.
также является изоморфизмом колец.


