Функция Мёбиуса. Формула обращения Мёбиуса
Функция Мёбиуса  натурального аргумента натурального аргумента  определяется следующим:образом: определяется следующим:образом:

Первые 13 значений 
Далее символ  означает, что суммирование распространяется на все натуральные делители означает, что суммирование распространяется на все натуральные делители  числа числа  . .
Лемма.

Доказательство. Для  утверждение очевидно. Пусть утверждение очевидно. Пусть  и и 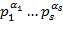 − каноническое разложение числа − каноническое разложение числа  . Тогда, учитывая, что делители . Тогда, учитывая, что делители  имеют вид имеют вид  , где , где  , ,  ,…, ,…,  ; ;  , получаем , получаем


поскольку

Теорема. (Аддитивная формула обращения Мёбиуса.) Пусть  и и  − функции натурального аргумента − функции натурального аргумента  . Тогда, если . Тогда, если

то

Доказательство. Имеем


Пусть  . Тогда . Тогда  прификсированном прификсированном  пробегает все значения делителей числа пробегает все значения делителей числа  . Это означает, что знаки суммирования в последней двойной сумме можно поменять местами, т.е. . Это означает, что знаки суммирования в последней двойной сумме можно поменять местами, т.е.

Теперь, учитывая, что

получаем
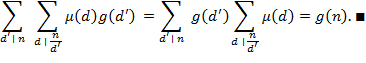
Имеется другая форма доказанной теоремы:
Теорема. (Мультипликативная формула обращения Мёбиуса.) Пусть

где символ  обозначает произведение, распространенное на все делители обозначает произведение, распространенное на все делители  числа числа  . .
Тогда

Доказательство:

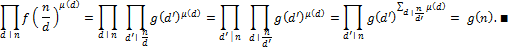
Примеры использования формулы обращения Мёбиуса:
 . Задача о числе кольцевых последовательностей. См.: Холл М. Комбинаторика. . Задача о числе кольцевых последовательностей. См.: Холл М. Комбинаторика.  М.: Мир, М.: Мир,  , § , §  . .
 . Число неприводимых многочленов заданной степени над конечным полем . Число неприводимых многочленов заданной степени над конечным полем  из из  элементов. См.: Берлекэмп Э. Алгебраическая теория кодирования. − М.: Мир, 1970, Гл. 3. элементов. См.: Берлекэмп Э. Алгебраическая теория кодирования. − М.: Мир, 1970, Гл. 3.
Глухов М. М., Елизаров В. П., Нечаев А. А. Алгебра. В 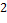 -х т. -х т.  М.: Гелиос, М.: Гелиос, 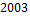 . Т. . Т. 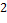 , § , § 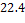 . .
Для самостоятельного изучения:
Обращение Мёбиуса на частично упорядоченных множествах. Принцип включения-исключения как частный случай формулы обращения Мёбиуса. См.: Холл М. Комбинаторика.  М.: Мир, М.: Мир,  , § , § 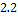 ; Бендер Э., Гольдман Дж. О приложениях обращения Мёбиуса в комбинаторном анализе. ; Бендер Э., Гольдман Дж. О приложениях обращения Мёбиуса в комбинаторном анализе.  В кн.: Перечислительные задачи комбинаторного анализа. В кн.: Перечислительные задачи комбинаторного анализа.  М.: Мир, 1971. М.: Мир, 1971.  С. С. 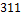 - -  . .
Сравнения для чисел сочетаний
Пусть  − простое число. − простое число.
Лемма.

Доказательство. При  числитель в формуле числитель в формуле


Следствие.

Доказательство.

Лемма. Пусть  , ,  , ,  , ,  − неотрицательные целые числа, причем − неотрицательные целые числа, причем  , , 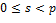 . Тогда . Тогда

Доказательство. Имеем

С другой стороны,


Сравнивая коэффициенты при одинаковых степенях  , получаем требуемый результат. ∎ , получаем требуемый результат. ∎
Пусть
 , ,  ; ;
 , , 
− представления неотрицательных целых чисел  и и  по основанию по основанию  . (Здесь . (Здесь  любое целое, при котором любое целое, при котором  , ,  ). На множестве неотрицательных целых чисел определим отношение частичного порядка (отношение предшествования) ). На множестве неотрицательных целых чисел определим отношение частичного порядка (отношение предшествования) 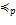 , полагая , полагая  , тогда и только тогда, когда , тогда и только тогда, когда
 , ,  ,…, ,…, 
Теорема Лукаса (  ). ).

Доказательство. Согласно предыдущей лемме,

где   , ,  . Применяя лемму повторно к . Применяя лемму повторно к  надлежащее число раз, получаем требуемый результат. ∎ надлежащее число раз, получаем требуемый результат. ∎
Замечание. Теорема не верна для непростых  . Например (см. Берлекэмп, с. . Например (см. Берлекэмп, с.  ), ),


Следствие.

II. Алгебраические структуры
II. 1. Множества с бинарными операциями. Группоиды, полугруппы, моноиды
Бинарной алгебраической операцией (или законом композиции) на непустом множестве S называется отображение  : :  , сопоставляющее паре , сопоставляющее паре 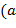 , , 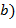 элементов элементов  , ,  однозначно определённый элемент однозначно определённый элемент  , ,  . На множестве . На множестве 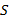 может быть задано много операций может быть задано много операций  . (Если, например, . (Если, например, 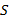 конечно, то число способов равно конечно, то число способов равно  , где , где  − число элементов в − число элементов в 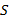 .) Желая выделить одну их них, например, .) Желая выделить одну их них, например,  , пишут , пишут  , ,  . Такой объект называют бинарной алгеброй, или группоидом. Вместо . Такой объект называют бинарной алгеброй, или группоидом. Вместо  , ,  часто пишут часто пишут 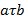 , а саму операцию обозначают каким-либо символом ( , а саму операцию обозначают каким-либо символом ( , ,  , ,  , ,  и т.п.). и т.п.).
Замечание. Наряду с бинарными операциями рассматривают более общие  -арные операции (унарные при -арные операции (унарные при  , тернарные при , тернарные при  и т.д.). Связанные с ними алгебраические структуры (системы) составляют предмет исследования т.н. универсальных алгебр. и т.д.). Связанные с ними алгебраические структуры (системы) составляют предмет исследования т.н. универсальных алгебр.
Бинарная операция  на множестве на множестве 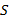 называется ассоциативной, если называется ассоциативной, если
 , для любых , для любых  , , 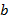 , ,  . .
Группоид с ассоциативной операцией называют полугруппой.
Пример неассоциативного группоида. На множестве  определим операцию определим операцию  как как  . Операция неассоциативна: . Операция неассоциативна:  , но , но  . .
Теорема. Если бинарная операция  на множестве на множестве  ассоциативна, то значение выражения ассоциативна, то значение выражения  не зависит от расстановки в нём скобок. не зависит от расстановки в нём скобок.
Доказательство. При  , , 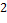 или или  утверждение очевидно. Для утверждение очевидно. Для 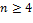 достаточно, применяя индукцию, показать, что достаточно, применяя индукцию, показать, что
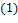 
для любых  , ,  . По предположению индукции расстановка скобок в . По предположению индукции расстановка скобок в
 не существенна; в частности, не существенна; в частности,  . .
Если  , то , то  . .
Если  , то , то
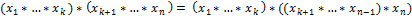
 . .
К такому же виду приводится и правая часть доказываемого равенства (1). ∎
Элемент  называется нейтральным относительно операции называется нейтральным относительно операции  , если , если
 для любого для любого  . .
Полугруппу  , ,  с элементом с элементом  называют моноидом (или полугруппой с единицей) и обозначают называют моноидом (или полугруппой с единицей) и обозначают  , ,  , ,  . .
В полугруппе (группоиде) может быть не более одного нейтрального элемента: если
 , ,  − нейтральные элементы, то − нейтральные элементы, то 
Группоид (полугруппу)  , ,  называют подгруппоидом (подполугруппой) группоида (полугруппы) называют подгруппоидом (подполугруппой) группоида (полугруппы)  , ,  , если , если
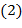  и и  для любых для любых  , , 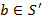 . .
В этом случае говорят, что подмножество  замкнуто относительно операции замкнуто относительно операции  . Моноид . Моноид  , ,  , ,  называют подмоноидом моноида называют подмоноидом моноида  , ,  , ,  , если выполняется , если выполняется 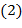 и и  . .
Элемент  моноида моноида  , ,  , ,  называется обратимым, если найдётся элемент называется обратимым, если найдётся элемент 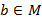 такой, что такой, что  (очевидно, что тогда и (очевидно, что тогда и 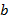 обратим). Если таким же свойством обладает и элемент обратим). Если таким же свойством обладает и элемент  , т.е. , т.е.  , то из равенств , то из равенств 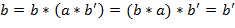 следует, что элемент следует, что элемент 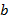 является на самом деле единственным (по отношению к является на самом деле единственным (по отношению к  ). Это позволяет говорить об обратном элементе ). Это позволяет говорить об обратном элементе  , к(обратимому) элементу , к(обратимому) элементу  , со свойствами: , со свойствами:  , ,  . .
Если  , , 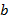 − обратимые элементы моноида − обратимые элементы моноида  , ,  , ,  , то их произведение , то их произведение  − также обратимый элемент, поскольку − также обратимый элемент, поскольку  , ,  . Очевидно, что . Очевидно, что  − обратимый элемент. Следовательно, имеет место − обратимый элемент. Следовательно, имеет место
Теорема. Множество всех обратимых элементов моноида  , ,  , ,  замкнуто относительно операции ∗ и образует подмоноид в замкнуто относительно операции ∗ и образует подмоноид в  , ,  , ,  . .
Группы
Определение группы. Моноид  , ,  , ,  , все элементы которого обратимы, называется группой. , все элементы которого обратимы, называется группой.
Другими словами, группа − это множество  с бинарной операцией с бинарной операцией  , для которых выполняются следующие аксиомы: , для которых выполняются следующие аксиомы:
 . (Замкнутость операции.) . (Замкнутость операции.)  , ,  . .
 . (Ассоциативность операции.) . (Ассоциативность операции.)  , , 
 . (Существование нейтрального элемента.) ∃ . (Существование нейтрального элемента.) ∃  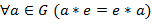 . .
 . (Существование обратного элемента.) . (Существование обратного элемента.)  . .
Замечание. Возвращаясь к введённым выше алгебраическим структурам, мы наблюдаем среди них следующую иерархию: пара  , ,  является группоидом, если выполняется аксиома является группоидом, если выполняется аксиома  ; полугруппой, если выполняются аксиомы ; полугруппой, если выполняются аксиомы  и и  ; моноидом, если выполняются аксиомы ; моноидом, если выполняются аксиомы  , ,  и и  ; группой, если выполняются аксиомы ; группой, если выполняются аксиомы  , ,  , ,  и и  . .
Удобно считать, что наряду с бинарной операцией в группе определена унарная операция взятия обратного  : :  , , 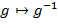 . Справедливы формулы: . Справедливы формулы:
 , ,  . .
Естественным образом определяются степени элементов с очевидными свойствами:
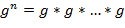 ( ( раз), раз),
 ( ( раз), раз), 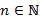 , ,
 ; ;  , ( , ( , ,  , ,  . .
Переставлять элементы в выражении  , вообще говоря, нельзя (т.е. , вообще говоря, нельзя (т.е.  ). Если ). Если 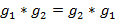 , то элементы называются перестановочными, или коммутирующими. Если любые два элемента , то элементы называются перестановочными, или коммутирующими. Если любые два элемента  группы коммутируют, то группа группы коммутируют, то группа  называется коммутативной, или абелевой (в честь норвежского математика Риль Хенрика Абеля ( называется коммутативной, или абелевой (в честь норвежского математика Риль Хенрика Абеля ( - -  )). )).
Операция в группе чаще всего обозначается либо символом  (сложение), либо символом (сложение), либо символом  (умножение). При этом группа называется соответственно аддитивной или мультипликативной, её нейтральный элемент − соответственно нулём ( (умножение). При этом группа называется соответственно аддитивной или мультипликативной, её нейтральный элемент − соответственно нулём ( ) или единицей ( ) или единицей ( ). В аддитивной группе элемент, элемент, обратный к элементу ). В аддитивной группе элемент, элемент, обратный к элементу  , называется противоположным и обозначается , называется противоположным и обозначается  , а вместо , а вместо  пишут пишут  . В мультипликативной группе вместо . В мультипликативной группе вместо  обычно пишут обычно пишут  , опуская символ операции. , опуская символ операции.
Примеры аддитивных групп. 1)  , ,  , ,  , ,  , , 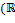 , ,  , ,  , ,  – аддитивные группы кольца – аддитивные группы кольца  и полей и полей 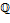 , , 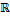 , ,  . Пишут просто . Пишут просто  , , 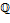 , , 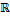 , ,  . 2) Любое кольцо . 2) Любое кольцо  по сложению − абелева группа. В частности, кольцо многочленов по сложению − абелева группа. В частности, кольцо многочленов  ,…, ,…,  ] и кольцо матриц ] и кольцо матриц  , ,  порядка порядка  над полем над полем  − абелевы группы. 3) Любое векторное пространство − абелевы группы. 3) Любое векторное пространство  над полем над полем  относительно сложения − абелева группа. 4) относительно сложения − абелева группа. 4)  , 1,…, , 1,…,  − полная система наименьших неотрицательных вычетов по модулю − полная система наименьших неотрицательных вычетов по модулю  с операцией сложения по модулю с операцией сложения по модулю  . .
Примеры мультипликативных групп. 1)  , ,  , ,  − мультипликативные группы полей − мультипликативные группы полей 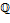 , , 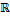 , ,  . 2) . 2) 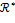 − множество обратимых элементов любого кольца − множество обратимых элементов любого кольца  с единицей относительно умножения. В частности, с единицей относительно умножения. В частности,  = =  ; ;  , ,  − множество обратимых матриц из − множество обратимых матриц из  . 3) . 3)  − − 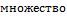 всех (вещественных и комплексных) корней всех (вещественных и комплексных) корней
 , ,  , 1,…, , 1,…,  , ,  − мнимая единица, − мнимая единица,
уравнения  − мультипликативная абелева группа. 4) − мультипликативная абелева группа. 4) 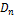 − множество вращений правильного − множество вращений правильного  -угольника в плоскости и в пространстве − некоммутативная группа (при -угольника в плоскости и в пространстве − некоммутативная группа (при  ). ).
Далее чаще используется мультипликативная форма записи операции. Группа обычно обозначается одной буквой без указания операции. Множество всех элементов группы  называется основным множеством группы и обозначается той же буквой называется основным множеством группы и обозначается той же буквой  . Если основное множество конечно, то группа называется конечной; в противном случае она называется бесконечной. Число элемент конечной группы называется её порядком. Группа . Если основное множество конечно, то группа называется конечной; в противном случае она называется бесконечной. Число элемент конечной группы называется её порядком. Группа  порядка 1 называется единичной, или т ривиальной. О бесконечной группе говорят, что она имеет бесконечный порядок. Для обозначения порядка группы (мощности основного множества) используются равноправные символы Card порядка 1 называется единичной, или т ривиальной. О бесконечной группе говорят, что она имеет бесконечный порядок. Для обозначения порядка группы (мощности основного множества) используются равноправные символы Card  (кардинальное число), (кардинальное число),  и ( и (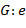 ). ).
Если 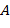 , ,  − подмножества (основного множества) группы, то полагаем − подмножества (основного множества) группы, то полагаем
 , ,  , ,  . .
Подгруппой группы  называется подмножество в называется подмножество в  само являющееся группой относительно той же операции, что и в само являющееся группой относительно той же операции, что и в  . Другими словами, подмножество . Другими словами, подмножество  является подгруппой тогда и только тогда, когда является подгруппой тогда и только тогда, когда  ( ( единица в единица в  ) и замкнуто относительно умножения и взятия обратного, т.е. ) и замкнуто относительно умножения и взятия обратного, т.е.  , ,  (на самом деле здесь даже равенства). Если (на самом деле здесь даже равенства). Если  − подгруппа в − подгруппа в  , то пишут , то пишут  ; если при этом ; если при этом  , то , то  называется собственной подгруппой и это обозначается как называется собственной подгруппой и это обозначается как  . .
Примеры.
|



 натурального аргумента
натурального аргумента  определяется следующим:образом:
определяется следующим:образом:

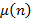

 означает, что суммирование распространяется на все натуральные делители
означает, что суммирование распространяется на все натуральные делители  числа
числа 
 утверждение очевидно. Пусть
утверждение очевидно. Пусть  и
и 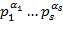 − каноническое разложение числа
− каноническое разложение числа  , где
, где  ,
,  ,…,
,…,  ;
;  , получаем
, получаем


 и
и  − функции натурального аргумента
− функции натурального аргумента 



 . Тогда
. Тогда  пробегает все значения делителей числа
пробегает все значения делителей числа  . Это означает, что знаки суммирования в последней двойной сумме можно поменять местами, т.е.
. Это означает, что знаки суммирования в последней двойной сумме можно поменять местами, т.е.

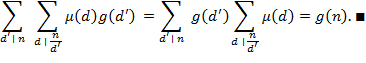

 обозначает произведение, распространенное на все делители
обозначает произведение, распространенное на все делители  числа
числа  .
.

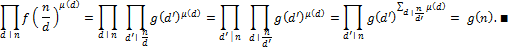
 . Задача о числе кольцевых последовательностей. См.: Холл М. Комбинаторика.
. Задача о числе кольцевых последовательностей. См.: Холл М. Комбинаторика.  М.: Мир,
М.: Мир,  , §
, §  .
.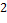 . Число неприводимых многочленов заданной степени над конечным полем
. Число неприводимых многочленов заданной степени над конечным полем  из
из  элементов. См.: Берлекэмп Э. Алгебраическая теория кодирования. − М.: Мир, 1970, Гл. 3.
элементов. См.: Берлекэмп Э. Алгебраическая теория кодирования. − М.: Мир, 1970, Гл. 3.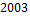 . Т.
. Т. 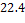 .
.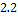 ; Бендер Э., Гольдман Дж. О приложениях обращения Мёбиуса в комбинаторном анализе.
; Бендер Э., Гольдман Дж. О приложениях обращения Мёбиуса в комбинаторном анализе.  М.: Мир, 1971.
М.: Мир, 1971.  С.
С. 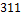 -
-  .
. − простое число.
− простое число.
 числитель в формуле
числитель в формуле



 ,
,  ,
,  ,
,  − неотрицательные целые числа, причем
− неотрицательные целые числа, причем  ,
, 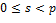 . Тогда
. Тогда



 , получаем требуемый результат. ∎
, получаем требуемый результат. ∎ ,
,  ;
; ,
, 
 и
и  . (Здесь
. (Здесь  любое целое, при котором
любое целое, при котором  ). На множестве неотрицательных целых чисел определим отношение частичного порядка (отношение предшествования)
). На множестве неотрицательных целых чисел определим отношение частичного порядка (отношение предшествования) 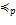 , полагая
, полагая  , тогда и только тогда, когда
, тогда и только тогда, когда ,
,  ,…,
,…, 
 ).
).


 ,
,  . Применяя лемму повторно к
. Применяя лемму повторно к  надлежащее число раз, получаем требуемый результат. ∎
надлежащее число раз, получаем требуемый результат. ∎ ),
),


 :
:  , сопоставляющее паре
, сопоставляющее паре 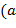 ,
, 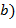 элементов
элементов  ,
,  однозначно определённый элемент
однозначно определённый элемент  ,
,  . На множестве
. На множестве 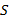 может быть задано много операций
может быть задано много операций  , где
, где  − число элементов в
− число элементов в  ,
,  . Такой объект называют бинарной алгеброй, или группоидом. Вместо
. Такой объект называют бинарной алгеброй, или группоидом. Вместо  ,
,  часто пишут
часто пишут 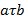 , а саму операцию обозначают каким-либо символом (
, а саму операцию обозначают каким-либо символом ( ,
,  ,
,  ,
,  и т.п.).
и т.п.). , тернарные при
, тернарные при  и т.д.). Связанные с ними алгебраические структуры (системы) составляют предмет исследования т.н. универсальных алгебр.
и т.д.). Связанные с ними алгебраические структуры (системы) составляют предмет исследования т.н. универсальных алгебр. , для любых
, для любых 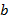 ,
,  .
. определим операцию
определим операцию  . Операция неассоциативна:
. Операция неассоциативна:  , но
, но  .
. на множестве
на множестве  ассоциативна, то значение выражения
ассоциативна, то значение выражения  не зависит от расстановки в нём скобок.
не зависит от расстановки в нём скобок. утверждение очевидно. Для
утверждение очевидно. Для 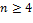 достаточно, применяя индукцию, показать, что
достаточно, применяя индукцию, показать, что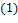

 ,
,  . По предположению индукции расстановка скобок в
. По предположению индукции расстановка скобок в не существенна; в частности,
не существенна; в частности,  .
. , то
, то  .
. , то
, то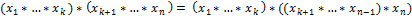
 .
. называется нейтральным относительно операции
называется нейтральным относительно операции  для любого
для любого  .
. с элементом
с элементом  называют моноидом (или полугруппой с единицей) и обозначают
называют моноидом (или полугруппой с единицей) и обозначают  .
. ,
,  − нейтральные элементы, то
− нейтральные элементы, то 
 ,
,  ,
, 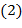
 и
и  для любых
для любых 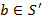 .
. замкнуто относительно операции
замкнуто относительно операции  ,
,  называют подмоноидом моноида
называют подмоноидом моноида  ,
,  .
.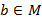 такой, что
такой, что  (очевидно, что тогда и
(очевидно, что тогда и  , т.е.
, т.е.  , то из равенств
, то из равенств 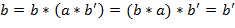 следует, что элемент
следует, что элемент  , к(обратимому) элементу
, к(обратимому) элементу  ,
,  .
. − также обратимый элемент, поскольку
− также обратимый элемент, поскольку  ,
,  . Очевидно, что
. Очевидно, что  ,
,  с бинарной операцией
с бинарной операцией  . (Замкнутость операции.)
. (Замкнутость операции.)  ,
,  .
. . (Ассоциативность операции.)
. (Ассоциативность операции.) 
 . (Существование нейтрального элемента.) ∃
. (Существование нейтрального элемента.) ∃ 
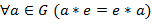 .
.  . (Существование обратного элемента.)
. (Существование обратного элемента.)  .
.  :
:  ,
, 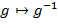 . Справедливы формулы:
. Справедливы формулы: ,
,  .
.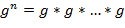 (
( (
(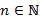 ,
, ;
;  , (
, ( ,
,  ,
,  .
. , вообще говоря, нельзя (т.е.
, вообще говоря, нельзя (т.е.  ). Если
). Если 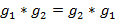 , то элементы называются перестановочными, или коммутирующими. Если любые два элемента
, то элементы называются перестановочными, или коммутирующими. Если любые два элемента  группы коммутируют, то группа
группы коммутируют, то группа  -
-  )).
)). ) или единицей (
) или единицей ( , называется противоположным и обозначается
, называется противоположным и обозначается  , а вместо
, а вместо  пишут
пишут  . В мультипликативной группе вместо
. В мультипликативной группе вместо  обычно пишут
обычно пишут  , опуская символ операции.
, опуская символ операции. ,
,  ,
,  ,
, 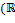 ,
,  ,
,  и полей
и полей 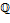 ,
, 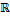 ,
,  . Пишут просто
. Пишут просто  по сложению − абелева группа. В частности, кольцо многочленов
по сложению − абелева группа. В частности, кольцо многочленов  ,…,
,…,  ] и кольцо матриц
] и кольцо матриц  ,
,  порядка
порядка  − абелевы группы. 3) Любое векторное пространство
− абелевы группы. 3) Любое векторное пространство  над полем
над полем  , 1,…,
, 1,…,  − полная система наименьших неотрицательных вычетов по модулю
− полная система наименьших неотрицательных вычетов по модулю  ,
,  ,
,  − мультипликативные группы полей
− мультипликативные группы полей 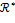 − множество обратимых элементов любого кольца
− множество обратимых элементов любого кольца  =
=  ;
;  ,
,  . 3)
. 3)  −
− 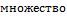 всех (вещественных и комплексных) корней
всех (вещественных и комплексных) корней ,
,  , 1,…,
, 1,…,  ,
,  − мнимая единица,
− мнимая единица, − мультипликативная абелева группа. 4)
− мультипликативная абелева группа. 4) 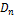 − множество вращений правильного
− множество вращений правильного  ).
). порядка 1 называется единичной, или т ривиальной. О бесконечной группе говорят, что она имеет бесконечный порядок. Для обозначения порядка группы (мощности основного множества) используются равноправные символы Card
порядка 1 называется единичной, или т ривиальной. О бесконечной группе говорят, что она имеет бесконечный порядок. Для обозначения порядка группы (мощности основного множества) используются равноправные символы Card  и (
и (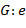 ).
). ,
,  − подмножества (основного множества) группы, то полагаем
− подмножества (основного множества) группы, то полагаем ,
,  ,
,  .
. является подгруппой тогда и только тогда, когда
является подгруппой тогда и только тогда, когда  (
( единица в
единица в  ,
,  (на самом деле здесь даже равенства). Если
(на самом деле здесь даже равенства). Если  − подгруппа в
− подгруппа в  ; если при этом
; если при этом  , то
, то  .
.


