Интерполяционная формула Лагранжа.
Теорема. (Интерполяционная формула Лагранжа.) Пусть  ; ;  , ,  ,…, ,…,  − различные, и − различные, и  , , 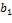 ,…, ,…, 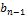 − любые элементы поля − любые элементы поля  . Тогда существует в точности один многочлен . Тогда существует в точности один многочлен  степени степени  такой, что такой, что  для для  , ,  ,…, ,…,  . Этот многочлен имеет вид . Этот многочлен имеет вид

Доказательство. Так как  при при 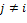 и и  , то , то  для для  . .
Пусть 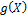 − другой многочлен, обладающий теми же свойствами, что и − другой многочлен, обладающий теми же свойствами, что и 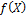 . Тогда многочлен . Тогда многочлен  степени степени  имеет имеет  корней. Значит, корней. Значит,  − нулевой многочлен, и − нулевой многочлен, и 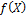 − единственный многочлен с требуемыми свойствами. ∎ − единственный многочлен с требуемыми свойствами. ∎
Другие формулы. Если  − конечное поле, то − конечное поле, то

Дискретное преобразование Фурье. Если 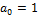 , ,  ,…, ,…,  , где , где  − элемент порядка − элемент порядка  мультипликативной группы поля мультипликативной группы поля  , ,  , то , то

Поле отношений. ( вкратце )
Имеется много общих свойств между кольцами  и и 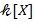 . Наша дальнейшая цель вложить . Наша дальнейшая цель вложить 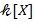 в поле, так же, как в поле, так же, как  вкладывается в вкладывается в  . .
Пусть 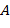 − целостное кольцо. Рассмотрим множество пар ( − целостное кольцо. Рассмотрим множество пар ( , , 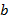 ) ∈ ) ∈   , где , где   . Пары ( . Пары ( , , 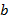 ) будем называть дробями и обозначать через ) будем называть дробями и обозначать через  (что более привычно). На множестве дробей определим отношение равенства: (что более привычно). На множестве дробей определим отношение равенства:

Нетрудно проверить, что данное отношение обладает следующими свойствами:



Первые два свойства очевидны. Докажем третье свойство:

Таким образом, отношение равенства является отношением эквивалентности на множестве   и, следовательно, определяет разбиение этого множества на непересекающиеся классы. Класс эквивалентности, содержащий дробь и, следовательно, определяет разбиение этого множества на непересекающиеся классы. Класс эквивалентности, содержащий дробь  , обозначим через , обозначим через  . Так что . Так что

На множество классов, которое обозначим через  , можно перенести обычные операции сложения и умножения: , можно перенести обычные операции сложения и умножения:

Нетрудно показать, что эти операции определены корректно, т.е. не зависят от выбора представителей классов, а именно:

Нетрудно проверить также, что множество  относительно введённых операций сложения и умножения дробей образует поле. Чтобы оно содержало кольцо относительно введённых операций сложения и умножения дробей образует поле. Чтобы оно содержало кольцо 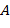 нужно отождествить некоторые дроби с элементами из нужно отождествить некоторые дроби с элементами из 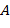 . Это достигается следующим образом. Элементу . Это достигается следующим образом. Элементу 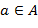 отнесём дроби отнесём дроби  , где , где 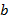 − любой элемент из − любой элемент из  (на самом деле элементу (на самом деле элементу 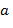 будет отнесена одна дробь, поскольку все дроби будет отнесена одна дробь, поскольку все дроби  равны). Далее квадратные скобки в записи равны). Далее квадратные скобки в записи  будем опускать. будем опускать.
Поле ( , +, ∙) называется полем отношений, или полем частных кольца , +, ∙) называется полем отношений, или полем частных кольца 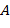 . Таким образом, доказано существование объемлющего поля для целостного кольца. Заметим, что кольцо могло и не содержать единицу, а в поле частных она появится. (Пример: . Таким образом, доказано существование объемлющего поля для целостного кольца. Заметим, что кольцо могло и не содержать единицу, а в поле частных она появится. (Пример:  , где , где  , ,  .) .)
Конструкция полей отношений часто используется в математике. Например, поле рациональных чисел  есть не что иное, как поле отношений есть не что иное, как поле отношений  кольца кольца  . Нетрудно проверить также, что . Нетрудно проверить также, что  , если , если 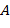 − поле. − поле.
Другой важный пример полей отношений даёт кольцо  , где , где  – поле (в более общем случае – поле (в более общем случае  ,…, ,…,  − кольцо многочленов от переменных). Поле отношений − кольцо многочленов от переменных). Поле отношений  кольца кольца 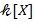 называется полем рациональных дробей от переменной называется полем рациональных дробей от переменной  с коэффициентами в с коэффициентами в  и обозначается через и обозначается через  (квадратные скобки меняются на круглые). (квадратные скобки меняются на круглые).
Поле  бесконечно и имеет характеристику, совпадающую с характеристикой поля бесконечно и имеет характеристику, совпадающую с характеристикой поля  . Каждая рациональная дробь записывается в виде . Каждая рациональная дробь записывается в виде  , где , где  , ,  − многочлены из − многочлены из 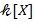 , ,  − ненулевой многочлен; − ненулевой многочлен;  называется числителем, а называется числителем, а  − знаменателем дроби − знаменателем дроби  . Дробь не меняется, если числитель и знаменатель умножить на один и тот же ненулевой многочлен или сократить на общий множитель. Значение . Дробь не меняется, если числитель и знаменатель умножить на один и тот же ненулевой многочлен или сократить на общий множитель. Значение  не зависит от представления дроби не зависит от представления дроби  в виде отношения (частного) двух многочленов в виде отношения (частного) двух многочленов  и и  . Рациональная дробь называется несократимой, если её числитель взаимно прост со знаменателем. Любая рациональная дробь . Рациональная дробь называется несократимой, если её числитель взаимно прост со знаменателем. Любая рациональная дробь  однозначно представляется несократимой дробью однозначно представляется несократимой дробью  , где , где  и и  − частные от деления − частные от деления  и и  на их наибольший общий делитель нод на их наибольший общий делитель нод  , ,  . Старший коэффициент знаменателя можно вынести и его обратное значение присоединить к числителю. Несократимая дробь со знаменателем, являющимся унитарным многочленом, называется нормализованной. Если deg . Старший коэффициент знаменателя можно вынести и его обратное значение присоединить к числителю. Несократимая дробь со знаменателем, являющимся унитарным многочленом, называется нормализованной. Если deg  , т.е. степень числителя меньше степени знаменателя, то несократимая дробь называется правильной. , т.е. степень числителя меньше степени знаменателя, то несократимая дробь называется правильной.
Теорема. Каждая рациональная дробь из  представима в виде суммы многочлена и правильной лроби. представима в виде суммы многочлена и правильной лроби.
Доказательство. Использовать теорему о делении с остатком. ∎
Определение. Правильная рациональная дробь  из из  называется простейшей, если называется простейшей, если  , ,  , где , где  − неприводимый многочлен, и deg − неприводимый многочлен, и deg  . .
Теорема. Каждая правильная рациональная дробь  из из  может быть разложена в сумму простейших дробей, причём единственным способом. может быть разложена в сумму простейших дробей, причём единственным способом.
Конкретно, если 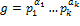 – каноническое разложение многочлена – каноническое разложение многочлена  в произведение неприводимых сомножителей в произведение неприводимых сомножителей  , ,  , ,  (многочлены (многочлены  , ,  , ,  , ,  − унитарные), то − унитарные), то

для некоторых 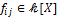 , ,  . .
Доказательство. Опускается. ∎
Элементы теории полей.
Если  − подполе поля − подполе поля 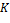 , то , то 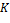 называют расширением поля называют расширением поля  . Далее запись . Далее запись  означает, что означает, что 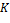 − расширение поля − расширение поля  . Если . Если  − подполе поля − подполе поля  , а , а  − подполе поля − подполе поля 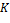 , т.е. , т.е.  , то , то  называют промежуточным полем расширения называют промежуточным полем расширения  . Цепочку расширений . Цепочку расширений
 , ,
где  − промежуточное поле расширения − промежуточное поле расширения  , , 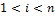 , называют , называют  - этажной башней полей. - этажной башней полей.
Любое расширение  можно рассматривать как векторное пространство над полем можно рассматривать как векторное пространство над полем  (относительно сложения в (относительно сложения в 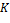 и умножения на элементы поля и умножения на элементы поля  ). Размерность ). Размерность  этого пространства называют степенью расширения этого пространства называют степенью расширения  и обозначают и обозначают  . Если эта степень конечна, то расширение называют конечным, в противном случае − бесконечным. Всякий базис поля . Если эта степень конечна, то расширение называют конечным, в противном случае − бесконечным. Всякий базис поля 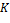 как векторного пространства над как векторного пространства над  называют базисом расширения называют базисом расширения  . .
Теорема. Пусть  − промежуточное поле расширения − промежуточное поле расширения  . Расширение . Расширение  конечно тогда и только тогда, когда конечны расширения конечно тогда и только тогда, когда конечны расширения  и и  . В случае их конечности . В случае их конечности
 , ,
причём если  ,…, ,…,  − базис расширения − базис расширения  и и  ,…, ,…,  − базис расширения − базис расширения  , то элементы , то элементы  , ,  , ,  , составляют базис расширения , составляют базис расширения  . .
Доказательство. Предположим сначала, что расширения  и и  конечны. Тогда любой элемент конечны. Тогда любой элемент  записывается в виде записывается в виде
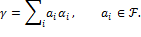
В свою очередь,

Следовательно,
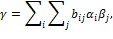
т.е.  − линейная комбинация над − линейная комбинация над  элементов элементов  . Предположим, что элементы . Предположим, что элементы  линейно зависимы над линейно зависимы над  , т.е. , т.е.  при некоторых при некоторых 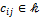 , не равных нулю одновременно. Тогда , не равных нулю одновременно. Тогда

для всех 1 ≤ 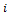 ≤ ≤  , 1 ≤ j ≤ , 1 ≤ j ≤  , поскольку элементы , поскольку элементы  ,…, ,…,  линейно независимы над линейно независимы над  , а элементы , а элементы  ,…, ,…,  линейно независимы над линейно независимы над  . Другими словами, элементы . Другими словами, элементы  составляют базис расширения составляют базис расширения  и и  . .
Обратно, если 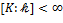 , то и , то и  , поскольку , поскольку  − подпространство в − подпространство в  . Если . Если  , ,  , ,  − базис пространства − базис пространства 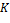 над над  , то произвольный элемент , то произвольный элемент  будет линейной комбинацией элементов будет линейной комбинацией элементов  , ,  , ,  с коэффициентами из с коэффициентами из  и, ввиду и, ввиду  , тем более с коэффициентами из , тем более с коэффициентами из  . Поэтому . Поэтому  . ∎ . ∎
Определение. Пусть 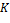 − расширение поля − расширение поля  , ,  . Элемент . Элемент  называется алгебраическим над (относительно) называется алгебраическим над (относительно)  , если он является корнем некоторого ненулевого многочлена , если он является корнем некоторого ненулевого многочлена  . Элемент . Элемент  , не являющийся алгебраическим над , не являющийся алгебраическим над  , называется т рансцендентным над , называется т рансцендентным над  . Расширение . Расширение  называется алгебраическим, если всякий элемент из называется алгебраическим, если всякий элемент из 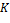 алгебраичен над алгебраичен над  . .
Теорема. Всякое конечное расширение  алгебраично над алгебраично над  . .
Доказательство. Пусть 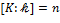 . Тогда степени . Тогда степени  , ,  , ,  , ,  , ,  любого элемента любого элемента
 линейно зависимы над линейно зависимы над  , т.е. , т.е.

при некоторых  , не равных нулю одновременно. Так что , не равных нулю одновременно. Так что  − корень некоторого ненулевого многочлена − корень некоторого ненулевого многочлена  . Значит, . Значит,  − алгебраический элемент над − алгебраический элемент над  . ∎ . ∎
Определение. Пусть 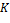 − расширение поля − расширение поля  и и  − алгебраический элемент над − алгебраический элемент над  . Выберем среди всех ненулевых многочленов . Выберем среди всех ненулевых многочленов  , для которых , для которых  , нормированный многочлен , нормированный многочлен  наименьшей степени. Он называется минимальным многочленом элемента наименьшей степени. Он называется минимальным многочленом элемента  относительно поля относительно поля  . Под степенью элемента . Под степенью элемента  над полем над полем  понимается степень его минимального многочлена. понимается степень его минимального многочлена.
Отметим следующие свойства минимального многочлена 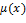 : :
1) если  и и  , то , то 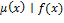 ; ;
2)  − неприводимый в − неприводимый в  многочлен. многочлен.
Действительно, 1) если  , то , то  − остаток от деления − остаток от деления  на на  − имел бы − имел бы  своим корнем, что противоречит выбору своим корнем, что противоречит выбору  , так как в этом случае , так как в этом случае  − ненулевой многочлен и deg − ненулевой многочлен и deg  . Далее, 2) если допустить, что . Далее, 2) если допустить, что  , где , где 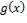 , , 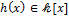 и и 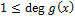 , ,  , то , то  является корнем либо является корнем либо 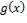 , либо , либо  , что также противоречит выбору , что также противоречит выбору  . .
Определение. Пусть  − подполе поля − подполе поля 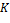 и и  − любое подмножество в − любое подмножество в 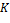 . Определим поле . Определим поле  как пересечение всех подполей поля как пересечение всех подполей поля 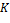 , содержащих одновременно , содержащих одновременно  и и  ; оно называется расширением поля ; оно называется расширением поля  , полученным присоединением элементов множества , полученным присоединением элементов множества  . Если . Если
 , ,  , ,  − конечное множество, то будем писать − конечное множество, то будем писать 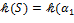 , ,  , ,  . Если . Если  состоит из одного элемента состоит из одного элемента  , то поле , то поле 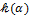 называется простым расширением поля называется простым расширением поля  , а , а  − образующим (или порождающим) элементом этого расширения. − образующим (или порождающим) элементом этого расширения.
Теорема. Пусть 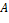 , , 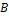 − любые подмножества расширения − любые подмножества расширения 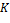 поля поля  . Тогда . Тогда
 . .
Доказательство. Поле  содержит поле содержит поле  и множество и множество 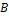 , а следовательно, и поле , а следовательно, и поле  . Обратно, поле . Обратно, поле  содержит множество содержит множество  , а следовательно, поле , а следовательно, поле  . ∎ . ∎
Следствие. Пусть  , ,  , ,  . Тогда . Тогда
 , ,  , ,  ). ).
Замечание. Отметим, что поле  , ,  , ,  образовано в точности дробями образовано в точности дробями

где  , ,  − многочлены от − многочлены от  переменных c коэффициентами из поля переменных c коэффициентами из поля  и и  , ,  , ,  ) ≠ 0. ) ≠ 0.
Уместно пояснить также, что записи  , ,  , ,  и и  , ,  , ,  отличаются тем, что круглые скобки обозначают всегда расширение до поля, т.е. образование всех рациональных выражений (дробей), а квадратные обозначают расширение до кольца, т.е. образование всех целых выражений отличаются тем, что круглые скобки обозначают всегда расширение до поля, т.е. образование всех рациональных выражений (дробей), а квадратные обозначают расширение до кольца, т.е. образование всех целых выражений  ,…, ,…,  . ∎ . ∎
Изучим строение простых расширений поля  . Далее два расширения . Далее два расширения 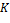 и и  поля поля  будем называть эквивалентными (относительно будем называть эквивалентными (относительно  ), если существует изоморфизм ), если существует изоморфизм   , переводящий элементы поля , переводящий элементы поля  в себя. в себя.
Теорема. Пусть 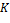 − расширение поля − расширение поля  , содержащее трансцендентный элемент , содержащее трансцендентный элемент  относительно поля относительно поля  . Тогда поле . Тогда поле 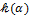 эквивалентно полю эквивалентно полю  рациональных дробей от переменной рациональных дробей от переменной  с коэффициентами в с коэффициентами в  . .
Доказательство. Напомним, что элементами поля  являются дроби являются дроби  , где , где  , ,  и и 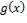 − ненулевой многочлен. При этом дроби − ненулевой многочлен. При этом дроби  и и  являются равными, т.е. представляют один и тот же элемент поля являются равными, т.е. представляют один и тот же элемент поля  , если , если  − нулевой многочлен. Поскольку − нулевой многочлен. Поскольку  для ненулевых многочленов, то для дроби для ненулевых многочленов, то для дроби  имеет смысл значение имеет смысл значение  . Разные дроби (как разные элементы поля . Разные дроби (как разные элементы поля  ) имеют разные значения в ) имеют разные значения в 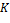 . Действительно, если . Действительно, если  = =  , то , то  , откуда следует, что , откуда следует, что
 − нулевой многочлен, и дроби − нулевой многочлен, и дроби  и и  представляют один и тот же элемент поля представляют один и тот же элемент поля  . Таким образом, между дробями . Таким образом, между дробями  и значениями и значениями  можно установить взаимно однозначное соответствие. Оно сохраняется и при операциях сложения и умножения: можно установить взаимно однозначное соответствие. Оно сохраняется и при операциях сложения и умножения:


Поскольку поле 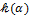 состоит в точности из элементов состоит в точности из элементов  , где , где  , ,  и и  − ненулевой многочлен, то поля − ненулевой многочлен, то поля  и и 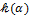 изоморфны. Установленный изоморфизм переводит элементы поля изоморфны. Установленный изоморфизм переводит элементы поля  в себя. Поэтому поля в себя. Поэтому поля  и и 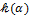 эквивалентны. ∎ эквивалентны. ∎
Теорема. Пусть 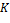 − расширение поля − расширение поля  , содержащее алгебраический элемент , содержащее алгебраический элемент  над над  , и пусть , и пусть  − минимальный многочлен элемента − минимальный многочлен элемента  степени степени  . Тогда: . Тогда:
1) простое алгебраическое расширение 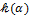 эквивалентно факторкольцу эквивалентно факторкольцу 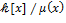 ; ;
2) [  ] = ] =  и {1, и {1,  , …, , …,  − базис векторного пространства − базис векторного пространства 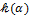 над над  ; ;
3) каждый элемент 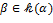 алгебраичен над алгебраичен над  , и его степень , и его степень  − делитель числа − делитель числа  . .
Доказательство. 1) Рассмотрим отображение  , определяемое следующим образом: , определяемое следующим образом: 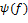 = =  для любого для любого  ∈ ∈  . Очевидно, что . Очевидно, что  является гомоморфизмом колец, и Ker является гомоморфизмом колец, и Ker  = { = {  ∈ ∈  }= ( }= ( ). Пусть ). Пусть  − образ отображения − образ отображения  , т.е. множество значений многочленов , т.е. множество значений многочленов  ∈ ∈  при при  . Отметим, что . Отметим, что
 и и  . .
Согласно теореме о гомоморфизмах колец имеем  . Так как . Так как 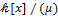 – поле (см.), то и – поле (см.), то и  – поле, но тогда, по определению простого расширения, – поле, но тогда, по определению простого расширения, 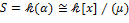 . Очевидно, что поля . Очевидно, что поля  и и 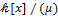 не только изоморфны, но и эквивалентны. не только изоморфны, но и эквивалентны.
2) Так как 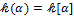 , то любой элемент , то любой элемент 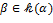 можно записать в виде можно записать в виде  для некоторого для некоторого  . Пусть . Пусть  − остаток от деления − остаток от деления  на на  . Тогда . Тогда  = =  . Так как . Так как  , то , то  является линейной комбинацией элементов является линейной комбинацией элементов  , ,  , ,  , ,  с коэффициентами из с коэффициентами из  . Остаётся показать, что элементы . Остаётся показать, что элементы  , ,  , ,  , ,  линейно независимы над линейно независимы над  . Для этого предположим противное: пусть . Для этого предположим противное: пусть
 , ,
где  и не все и не все  . Полагая . Полагая  , имеем: , имеем:  − ненулевой многочлен, − ненулевой многочлен,  и и  , но это противоречит выбору минимального многочлена , но это противоречит выбору минимального многочлена  . Следовательно, элементы . Следовательно, элементы  , ,  , ,  , ,  линейно независимы над линейно независимы над  и и 
3) Так как 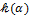 − конечное расширение поля − конечное расширение поля  , то любой элемент , то любой элемент 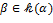 алгебраичен над алгебраичен над  . Пусть . Пусть  − степень элемента − степень элемента  над над  . Тогда, учитывая теорему и тот факт, что . Тогда, учитывая теорему и тот факт, что  − подполе поля − подполе поля  , имеем , имеем
 , ,
откуда следует, что  . ∎ . ∎
Теорема. Пусть  и и  − два расширения поля − два расширения поля  , и пусть , и пусть  и и  − алгебраические над полем − алгебраические над полем  элементы, имеющие олин и тот же минимальный многочлен элементы, имеющие олин и тот же минимальный многочлен  степени степени  . Тогда отображение . Тогда отображение

|



 ;
;  ,
,  ,…,
,…,  − различные, и
− различные, и  ,
, 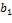 ,…,
,…, 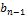 − любые элементы поля
− любые элементы поля  . Тогда существует в точности один многочлен
. Тогда существует в точности один многочлен  степени
степени  такой, что
такой, что  для
для  ,
,  ,…,
,…,  . Этот многочлен имеет вид
. Этот многочлен имеет вид
 при
при 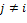 и
и  , то
, то  .
.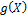 − другой многочлен, обладающий теми же свойствами, что и
− другой многочлен, обладающий теми же свойствами, что и 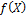 . Тогда многочлен
. Тогда многочлен  степени
степени  корней. Значит,
корней. Значит,  − нулевой многочлен, и
− нулевой многочлен, и  − конечное поле, то
− конечное поле, то
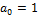 ,
,  ,…,
,…,  , где
, где  − элемент порядка
− элемент порядка  ,
,  , то
, то
 и
и 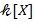 . Наша дальнейшая цель вложить
. Наша дальнейшая цель вложить  .
.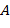 − целостное кольцо. Рассмотрим множество пар (
− целостное кольцо. Рассмотрим множество пар ( ,
, 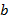 ) ∈
) ∈ 
 , где
, где 
 . Пары (
. Пары ( (что более привычно). На множестве дробей определим отношение равенства:
(что более привычно). На множестве дробей определим отношение равенства:





 . Так что
. Так что
 , можно перенести обычные операции сложения и умножения:
, можно перенести обычные операции сложения и умножения:

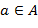 отнесём дроби
отнесём дроби  , где
, где 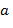 будет отнесена одна дробь, поскольку все дроби
будет отнесена одна дробь, поскольку все дроби  равны). Далее квадратные скобки в записи
равны). Далее квадратные скобки в записи  , где
, где  ,
,  .)
.) кольца
кольца  , если
, если  , где
, где  – поле (в более общем случае
– поле (в более общем случае  ,…,
,…,  − кольцо многочленов от переменных). Поле отношений
− кольцо многочленов от переменных). Поле отношений  кольца
кольца  с коэффициентами в
с коэффициентами в  (квадратные скобки меняются на круглые).
(квадратные скобки меняются на круглые). , где
, где  ,
,  − многочлены из
− многочлены из  не зависит от представления дроби
не зависит от представления дроби  , где
, где  и
и  − частные от деления
− частные от деления  ,
,  . Старший коэффициент знаменателя можно вынести и его обратное значение присоединить к числителю. Несократимая дробь со знаменателем, являющимся унитарным многочленом, называется нормализованной. Если deg
. Старший коэффициент знаменателя можно вынести и его обратное значение присоединить к числителю. Несократимая дробь со знаменателем, являющимся унитарным многочленом, называется нормализованной. Если deg  , т.е. степень числителя меньше степени знаменателя, то несократимая дробь называется правильной.
, т.е. степень числителя меньше степени знаменателя, то несократимая дробь называется правильной. представима в виде суммы многочлена и правильной лроби.
представима в виде суммы многочлена и правильной лроби. из
из  ,
,  − неприводимый многочлен, и deg
− неприводимый многочлен, и deg  .
.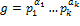 – каноническое разложение многочлена
– каноническое разложение многочлена  в произведение неприводимых сомножителей
в произведение неприводимых сомножителей  ,
,  ,
,  (многочлены
(многочлены 
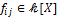 ,
,  .
. − подполе поля
− подполе поля 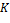 , то
, то  означает, что
означает, что  , то
, то  ,
, − промежуточное поле расширения
− промежуточное поле расширения  ,
, 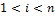 , называют
, называют  этого пространства называют степенью расширения
этого пространства называют степенью расширения  . Если эта степень конечна, то расширение называют конечным, в противном случае − бесконечным. Всякий базис поля
. Если эта степень конечна, то расширение называют конечным, в противном случае − бесконечным. Всякий базис поля  и
и  . В случае их конечности
. В случае их конечности ,
, ,…,
,…,  − базис расширения
− базис расширения  ,…,
,…,  − базис расширения
− базис расширения  ,
,  ,
,  , составляют базис расширения
, составляют базис расширения  записывается в виде
записывается в виде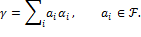

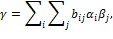
 − линейная комбинация над
− линейная комбинация над  при некоторых
при некоторых 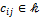 , не равных нулю одновременно. Тогда
, не равных нулю одновременно. Тогда
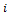 ≤
≤  , 1 ≤ j ≤
, 1 ≤ j ≤  , поскольку элементы
, поскольку элементы  .
.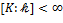 , то и
, то и  , поскольку
, поскольку  − подпространство в
− подпространство в  ,
,  − базис пространства
− базис пространства  , тем более с коэффициентами из
, тем более с коэффициентами из  . ∎
. ∎ . Элемент
. Элемент  . Элемент
. Элемент 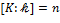 . Тогда степени
. Тогда степени  ,
,  ,
,  любого элемента
любого элемента
 , не равных нулю одновременно. Так что
, не равных нулю одновременно. Так что  . Значит,
. Значит,  , нормированный многочлен
, нормированный многочлен  наименьшей степени. Он называется минимальным многочленом элемента
наименьшей степени. Он называется минимальным многочленом элемента 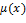 :
: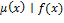 ;
; − неприводимый в
− неприводимый в  многочлен.
многочлен. , то
, то  − остаток от деления
− остаток от деления  на
на  . Далее, 2) если допустить, что
. Далее, 2) если допустить, что  , где
, где 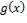 ,
, 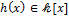 и
и 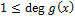 ,
,  , то
, то  , что также противоречит выбору
, что также противоречит выбору  − любое подмножество в
− любое подмножество в  как пересечение всех подполей поля
как пересечение всех подполей поля  ,
,  − конечное множество, то будем писать
− конечное множество, то будем писать 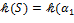 ,
,  . Если
. Если 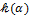 называется простым расширением поля
называется простым расширением поля  ,
,  − любые подмножества расширения
− любые подмножества расширения  .
. содержит поле
содержит поле  и множество
и множество  . Обратно, поле
. Обратно, поле  содержит множество
содержит множество  , а следовательно, поле
, а следовательно, поле  . Тогда
. Тогда ,
,  ).
).
 ,
,  ,
,  ) ≠ 0.
) ≠ 0. ,
,  отличаются тем, что круглые скобки обозначают всегда расширение до поля, т.е. образование всех рациональных выражений (дробей), а квадратные обозначают расширение до кольца, т.е. образование всех целых выражений
отличаются тем, что круглые скобки обозначают всегда расширение до поля, т.е. образование всех рациональных выражений (дробей), а квадратные обозначают расширение до кольца, т.е. образование всех целых выражений  ,…,
,…,  поля
поля 
 рациональных дробей от переменной
рациональных дробей от переменной  с коэффициентами в
с коэффициентами в  , где
, где  и
и  и
и  являются равными, т.е. представляют один и тот же элемент поля
являются равными, т.е. представляют один и тот же элемент поля  − нулевой многочлен. Поскольку
− нулевой многочлен. Поскольку  для ненулевых многочленов, то для дроби
для ненулевых многочленов, то для дроби  . Разные дроби (как разные элементы поля
. Разные дроби (как разные элементы поля  =
=  , то
, то  , откуда следует, что
, откуда следует, что и значениями
и значениями  можно установить взаимно однозначное соответствие. Оно сохраняется и при операциях сложения и умножения:
можно установить взаимно однозначное соответствие. Оно сохраняется и при операциях сложения и умножения:

 и
и  − минимальный многочлен элемента
− минимальный многочлен элемента 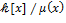 ;
; ] =
] =  − базис векторного пространства
− базис векторного пространства 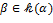 алгебраичен над
алгебраичен над  − делитель числа
− делитель числа  , определяемое следующим образом:
, определяемое следующим образом: 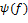 =
=  для любого
для любого  является гомоморфизмом колец, и Ker
является гомоморфизмом колец, и Ker  }= (
}= ( ). Пусть
). Пусть  − образ отображения
− образ отображения  ∈
∈  . Отметим, что
. Отметим, что и
и  .
. . Так как
. Так как 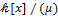 – поле (см.), то и
– поле (см.), то и 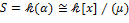 . Очевидно, что поля
. Очевидно, что поля  и
и 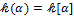 , то любой элемент
, то любой элемент  для некоторого
для некоторого  − остаток от деления
− остаток от деления  на
на  . Так как
. Так как  , то
, то  является линейной комбинацией элементов
является линейной комбинацией элементов  с коэффициентами из
с коэффициентами из  ,
, и не все
и не все  . Полагая
. Полагая  , имеем:
, имеем:  − ненулевой многочлен,
− ненулевой многочлен,  и
и  , но это противоречит выбору минимального многочлена
, но это противоречит выбору минимального многочлена 
 − подполе поля
− подполе поля  ,
, . ∎
. ∎ − два расширения поля
− два расширения поля  − алгебраические над полем
− алгебраические над полем 



