
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые результаты о многочленах над конечными полями.Содержание книги
Поиск на нашем сайте
Теорема. Если Доказательство. Пусть
Теорема. Каждый многочлен Доказательство. Если Теорема. Каждый делитель Доказательство. Пусть deg
Но
т.е. Теорема. Пусть Доказательство. По теореме Теорема. Пусть Доказательство. По теореме элементы
Получается, что порядок Теорема. Все корни неприводимого многочлена имеют один и тот же порядок. Доказательство. Пусть
следует, что Определение. Порядок корней неприводимого многочлена называется показателем, которому данный многочлен принадлежит. Если неприводимый многочлен принадлежит показателю
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.101 (0.005 с.) |

 − корень многочлена
− корень многочлена  , то
, то  также является корнем многочлена
также является корнем многочлена  .
. . Тогда
. Тогда . ∎
. ∎ , неприводимый над
, неприводимый над  , является делителем многочлена
, является делителем многочлена  .
. , то теорема верна. Пусть
, то теорема верна. Пусть  и
и  – корень многочлена
– корень многочлена  . Это расширение является полем
. Это расширение является полем  и совокупность его ненулевых элементов образует группу порядка
и совокупность его ненулевых элементов образует группу порядка  . Поэтому порядок элемента
. Поэтому порядок элемента  . Тогда по теореме многочлен
. Тогда по теореме многочлен  . Рассмотрим расширение
. Рассмотрим расширение 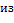
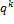 элементов, каждый из которых может быть представлен в виде линейной комбинации
элементов, каждый из которых может быть представлен в виде линейной комбинации  , где
, где  ,
,  ,…,
,…,  ∈
∈ 
 . Отсюда следует, что
. Отсюда следует, что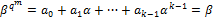 ,
, корень многочлена
корень многочлена  равно
равно  , то
, то  и, следовательно,
и, следовательно,  . ∎
. ∎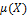 − минимальный многочлен над
− минимальный многочлен над  , то порядок элемента
, то порядок элемента  .
. . Тогда
. Тогда  , а
, а  . ∎
. ∎ образуют совокупность всех корней многочлена
образуют совокупность всех корней многочлена  при
при . Тогда
. Тогда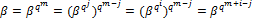 ,
, .
.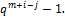 С другой стороны,
С другой стороны, 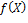 отличается от минимального многочлена для
отличается от минимального многочлена для  . Поэтому по теореме порядок
. Поэтому по теореме порядок  при некотором
при некотором 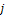 . Пусть
. Пусть  и
и  − порядки этих корней. Тогда из соотношений
− порядки этих корней. Тогда из соотношений ,
,
 и
и  . Но тогда
. Но тогда  . ∎
. ∎ , но не является делителем многочлена
, но не является делителем многочлена  при
при  . Неприводимый многочлен степени
. Неприводимый многочлен степени 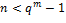 .
.


