

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Классы вычетов и факторкольца.
Пусть  − идеал кольца − идеал кольца  . Поскольку каждый идеал кольца является нормальной подгруппой аддитивной группы кольца, то идеал . Поскольку каждый идеал кольца является нормальной подгруппой аддитивной группы кольца, то идеал  задаёт некоторое разбиение множества задаёт некоторое разбиение множества  на смежные классы по аддитивной подгруппе на смежные классы по аддитивной подгруппе  . В данном случае эти классы называются классами вычетов кольца . В данном случае эти классы называются классами вычетов кольца 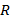 по модулю идеала по модулю идеала  . Соответствующее множество классов (фактор-множество) обозначим через . Соответствующее множество классов (фактор-множество) обозначим через  . Класс вычетов, содержащий элемент . Класс вычетов, содержащий элемент  , будем обозначать через , будем обозначать через  = =  ; он состоит из элементов вида ; он состоит из элементов вида  , , 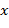 ∈ ∈  . Так как один и тот же класс может быть представлен разными элементами, то будет уместно напомнить, что . Так как один и тот же класс может быть представлен разными элементами, то будет уместно напомнить, что  ⟺ ⟺  . .
Лемма. Пусть  и и  . Тогда . Тогда  и и  . .
Доказательство. Из  и и  следует, что следует, что  и и  для некоторых для некоторых  , ,  . Тогда . Тогда
( )−( )−( = = 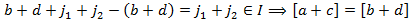 ; ;
 ∎ ∎
На элементах (классах) множества  определим операции ⊕ (сложение) и ⊙ (умножение), полагая: определим операции ⊕ (сложение) и ⊙ (умножение), полагая:
 , ,  . .
Из доказанной выше леммы следует, что эти операции определены корректно, т.е. не зависят от выбора представителей классов вычетов.
Теорема. Структура ( , ⊕, ⊙) является кольцом, которое называют факторкольцом кольца , ⊕, ⊙) является кольцом, которое называют факторкольцом кольца  по идеалу по идеалу  . .
Доказательство. Проверим выполнимость аксиом кольца. Тот факт, что ( , ⊕) –группа по существу уже доказан ранее в теореме. Сложение коммутативно: , ⊕) –группа по существу уже доказан ранее в теореме. Сложение коммутативно:
 . .
Значит, группа  , ,  абелева. Операция умножения ассоциативна: абелева. Операция умножения ассоциативна:
 . .
Дистрибутивные законы также выполняются:
( , ,
 . ∎ . ∎
Элементы  , ,  , принадлежащие одному и тому же классу вычетов по модулю идеала , принадлежащие одному и тому же классу вычетов по модулю идеала  , будем называть сравнимыми по модулю , будем называть сравнимыми по модулю  и записывать это как и записывать это как  . Отметим следующие свойства определённого сравнения: если . Отметим следующие свойства определённого сравнения: если   , то , то
 , ,  , , 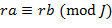 и и 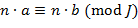
для любых  и и 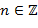 ; если, кроме того, ; если, кроме того,  , то , то  и и   . .
Пример. (Продолжение примера.) Пусть  , +, , +,  − кольцо целых чисел, − кольцо целых чисел,
 , ,  , ,  , где , где 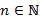 , − идеал (главный) в кольце , − идеал (главный) в кольце  , состоящий из чисел, кратных , состоящий из чисел, кратных  . Элементами кольца . Элементами кольца  , ,  , ,  являются те же смежные классы, что и в примере с операциями: являются те же смежные классы, что и в примере с операциями: 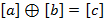 , ,  , где , где 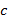 и и  − остатки от деления соответственно − остатки от деления соответственно 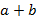 и и  на на  . Это кольцо называют кольцом целых чисел по модулю . Это кольцо называют кольцом целых чисел по модулю  и обозначают обычно через и обозначают обычно через  . .
О кольце  . .
Теорема. Кольцо  является полем тогда и только тогда, когда является полем тогда и только тогда, когда  − простое число. − простое число.
Доказательство. Пусть  − составное число, т.е. − составное число, т.е. 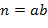 для некоторых целых для некоторых целых  , ,  . Тогда . Тогда  , откуда следует, что , откуда следует, что  − кольцо с делителями нуля. Значит, − кольцо с делителями нуля. Значит,  − не поле. − не поле.
Теперь предположим, что  − простое число. Пусть − простое число. Пусть  – любой ненулевой элемент. Так как – любой ненулевой элемент. Так как  при при  , то элементы , то элементы  , , 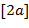 , …, , …,  различны и совпадают с элементами различны и совпадают с элементами  , ,  , …, , …,  (но, возможно, в другом порядке), то (но, возможно, в другом порядке), то
 ]. ].
На языке сравнений это означает, что  . Так как числа . Так как числа  , ,  , …, , …,  ) взаимно просты с ) взаимно просты с 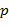 , то обе части полученного сравнения можно сократить на эти числа. В результате получаем , то обе части полученного сравнения можно сократить на эти числа. В результате получаем
 , ,
т.е. элемент  имеет обратный. Значит, имеет обратный. Значит, 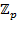 − поле. ∎ − поле. ∎
Из этой теоремы следует, что существуют поля, содержащие конечное число элементов. Они находят многочисленные применения в различных областях математики. Конечное поле, содержащее 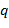 элементов, будем обозначать через элементов, будем обозначать через  (используют также обозначение (используют также обозначение 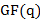 – от – от  − поле Галуа − по имени фр. математика Э. Галуа, заложившего фундаментальные основы теории групп). В частности, − поле Галуа − по имени фр. математика Э. Галуа, заложившего фундаментальные основы теории групп). В частности,  , если , если 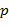 − простое число. Заметим, что − простое число. Заметим, что  и и  , как кольца с делителями нуля, не являются полями. Вместе с тем поле , как кольца с делителями нуля, не являются полями. Вместе с тем поле  существует, а поле существует, а поле  не существует. Далее будет установлено, при каких не существует. Далее будет установлено, при каких  существует поле существует поле  , и уточнено строение этих полей. , и уточнено строение этих полей.
Теорема (основная теорема о гомоморфизмах колец). Пусть 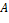 , , 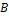 − −  . Тогда: . Тогда:
1) Если  − сюръективный гомоморфизм, то − сюръективный гомоморфизм, то  − идеал в − идеал в 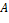 , а , а  . .
2) Обратно, если 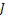 − идеал в − идеал в 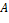 , то отображение , то отображение  , определяемое по правилу , определяемое по правилу  , является сюръективным гомоморфизмом с ядром , является сюръективным гомоморфизмом с ядром  . .
Гомоморфизм  называют естественным, или каноническим. называют естественным, или каноническим.
Доказательство. 1) Тот факт, что 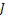 − идеал в − идеал в 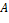 , доказан в лемме. Покажем, что изоморфизм между , доказан в лемме. Покажем, что изоморфизм между  и и 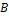 устанавливается с помощью отображения устанавливается с помощью отображения  , сопоставляющего классу вычетов , сопоставляющего классу вычетов  элемент элемент 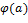 . Отображение . Отображение  определено корректно: если определено корректно: если  тот же класс вычетов. что и тот же класс вычетов. что и  , то , то  для некоторого для некоторого  и и
 , ,
так что значение  определено однозначно. Далее, если определено однозначно. Далее, если  , то , то  , поскольку в противном случае приходим к противоречию: , поскольку в противном случае приходим к противоречию:
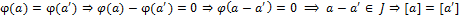 . .
Следовательно,  − инъекция. Поскольку − инъекция. Поскольку  сюръекция, т.е. сюръекция, т.е.  , то для любого , то для любого  найдётся найдётся 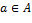 такой, что такой, что  . Отсюда следует, что и . Отсюда следует, что и  − сюръекция, но тогда − сюръекция, но тогда  − биекция. Кроме того, для любых − биекция. Кроме того, для любых 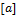 , ,  имеем имеем

и, аналогично,
 . .
Следовательно,  −изоморфизм. −изоморфизм.
2) Для любых  , ,  имеем имеем

и, аналогично,
 . .
Следовательно,  − гомоморфизм, очевидно, сюръективный. Так как − гомоморфизм, очевидно, сюръективный. Так как
 и и  , ,
то  . ∎ . ∎
Характеристика кольца (поля) .
Определение. Характеристикой кольца  называется наименьшее называется наименьшее 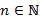 , при котором , при котором  для любого для любого  . Если такое . Если такое  существует, то кольцо существует, то кольцо  называется кольцом положительной характеристики называется кольцом положительной характеристики  . Если же такое . Если же такое  не существует, то говорят, что характеристика кольца не существует, то говорят, что характеристика кольца  равна нулю, а само равна нулю, а само  называют кольцом нулевой характеристики. называют кольцом нулевой характеристики.
Характеристика кольца  обозначается как Char обозначается как Char  . .
Примеры. 1) ℤ − кольцо, ℚ, ℝ, ℂ − поля нулевой характеристики. 2)  , где , где 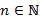 , − конечное кольцо положительной характеристики , − конечное кольцо положительной характеристики  . .
Если  − кольцо с единицей, то значение характеристики кольца полностью определяется аддитивными свойствами единицы: если − кольцо с единицей, то значение характеристики кольца полностью определяется аддитивными свойствами единицы: если  при любом при любом 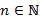 , то Char , то Char  ; если же существуют ; если же существуют  , при которых , при которых  , то Char , то Char  , где , где  − наименьшее из таких − наименьшее из таких  , поскольку , поскольку  ⟹ ⟹  = 0. = 0.
Теорема. Характеристика любого ненулевого кольца  с единицей и без делителей нуля равна либо нулю, либо некоторому простому числу с единицей и без делителей нуля равна либо нулю, либо некоторому простому числу 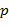 . .
Доказательство. Случай Char  возможен. Пусть Char возможен. Пусть Char  . Так как . Так как  содержит не менее двух элементов, то содержит не менее двух элементов, то 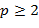 . Допустим на минутку, что . Допустим на минутку, что  − составное число, т.е. − составное число, т.е.  ,где ,где  , ,  − некоторые целые. Тогда из − некоторые целые. Тогда из 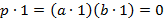 следует, что или следует, что или  , или , или  (либо и то, и другое). Пусть, для определённости, (либо и то, и другое). Пусть, для определённости,  , но тогда Char , но тогда Char  , что противоречит выбору числа , что противоречит выбору числа 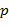 . Значит, . Значит, 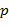 − простое число. ∎ − простое число. ∎
Теорема. (Равенство Шёнемана.) В коммутативном кольце  простой характеристики простой характеристики  имеет место тождество имеет место тождество
 для всех для всех 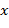 , ,  и и 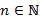 . .
Доказательство. Согласно лемме,  для любых для любых  и и  . Тогда . Тогда

Теперь, используя индукцию по  ,устанавливаем первое тождество: ,устанавливаем первое тождество:  , а из него вытекает второе: , а из него вытекает второе:  . ∎ . ∎
Следствие. При тех же предположениях
 для всех для всех  ,…, ,…,  и и  , ,  , ,
Определение. Подполем 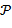 поля поля  называется подкольцо в называется подкольцо в  , само являющееся полем. , само являющееся полем.
Например,  − поле рациональных чисел − является подполем поля − поле рациональных чисел − является подполем поля  вещественных чисел, которое, в свою очередь, является подполем поля вещественных чисел, которое, в свою очередь, является подполем поля  комплексных чисел. комплексных чисел.
Если  , то говорят, что поле , то говорят, что поле  является расширением своего подполя является расширением своего подполя  (или надполем по отношению к (или надполем по отношению к 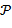 ). Из определения подполя следует, что нуль и единица поля ). Из определения подполя следует, что нуль и единица поля  лежат в лежат в 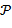 и также являются для и также являются для 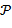 нулём и единицей. нулём и единицей.
Утверждение. Пересечение подполей  и и  поля поля  является подполем в является подполем в  . .
Доказательство. Проверить выполнимость аксиом поля для  ∩ ∩  . ∎ . ∎
Определение. Поле называется простым, если оно не содержит никаких подполей, отличных от него самого.
Примеры. 1) Поле 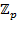 − простое поле для любого простого числа − простое поле для любого простого числа 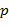 . Это следукт из того, что аддитивная группа . Это следукт из того, что аддитивная группа 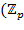 , ,  имеет простой порядок и по теореме Лагранжа не имеет собственных подгрупп. 2) имеет простой порядок и по теореме Лагранжа не имеет собственных подгрупп. 2)  − простое поле. В данном случае, наряду с числом 1, простое полполе поля − простое поле. В данном случае, наряду с числом 1, простое полполе поля  должно содержать все кратные ему, а также все дроби. Но это и будет множество должно содержать все кратные ему, а также все дроби. Но это и будет множество  . .
Отметим, что других простых полей, по существу отличающихся от указанных в примере, нет, о чём свидетельствует следующая
Теорема. Каждое поле  содержит только одно простое поле содержит только одно простое поле  , причём , причём  , если Char , если Char  , и , и  , если Char , если Char  . .
Доказательство. Допуская существование двух простых подполей  и и  поля поля  , мы неизбежно придём к противоречию, поскольку их пересечение , мы неизбежно придём к противоречию, поскольку их пересечение  содержится как в содержится как в  , так и в , так и в  , отлично от них и является подполем поля , отлично от них и является подполем поля  . Значит, простое поле . Значит, простое поле 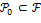 единственно. единственно.
Уточним структуру поля  . Это поле, как всякое подполе поля . Это поле, как всякое подполе поля  , содержит единицу , содержит единицу  поля поля  . Элементы вида . Элементы вида 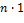 , ,  , с операциями , с операциями
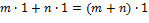 , , 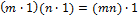 , ,  , ,  , ,
образуют коммутативное кольцо 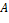 , являющееся подкольцом поля , являющееся подкольцом поля  . Рассмотрим отображение . Рассмотрим отображение
 , ,
определяемое правилом  . Это отображение является сюръективным гомоморфизмом кольца . Это отображение является сюръективным гомоморфизмом кольца  на кольцо на кольцо 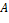 с ядром Ker с ядром Ker  . По теореме о гомоморфизмах колец . По теореме о гомоморфизмах колец  . Возможны два случая: . Возможны два случая:
  . В этом случае ядро тривиально, т.е. Ker . В этом случае ядро тривиально, т.е. Ker 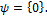 Следовательно, Следовательно,  − изоморфизм − изоморфизм  ) и дроби ) и дроби  , имеющие смысл в , имеющие смысл в  (поскольку (поскольку 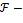 поле), образуют поле, изоморфное ℚ. Оно и будет простым подполем в поле), образуют поле, изоморфное ℚ. Оно и будет простым подполем в  . .
2.  . Поскольку . Поскольку  Char Char  − простое число, то − простое число, то  − поле. Так что − поле. Так что  ≅ ≅  − поле. Поскольку − поле. Поскольку  , то на самом деле , то на самом деле  . ∎ . ∎
Многочлены.
Пусть  − коммутативное кольцо с единицей − коммутативное кольцо с единицей  . .
Определение. Многочленом (или полиномом) над кольцом  называется формальное выражение вида называется формальное выражение вида

где 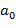 , …, , …,  − элементы кольца − элементы кольца  , называемые коэффициентами многочлена, , называемые коэффициентами многочлена, 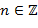 , ,  , ,  − некоторый (формальный) символ, не принадлежащий кольцу − некоторый (формальный) символ, не принадлежащий кольцу  , называемый переменной (или неизвестной). , называемый переменной (или неизвестной).
Замечание. Данное определение на самом деле не является достаточно строгим. В нём есть одно сомнительное место, касающееся связи коэффициентов  и посторонней переменной и посторонней переменной  . Этого вопроса обычно избегают. Однако можно дать совершенно безукоризненное определение многочлена как элемента кольца многочленов. Изложим его вкратце. (См.) . Этого вопроса обычно избегают. Однако можно дать совершенно безукоризненное определение многочлена как элемента кольца многочленов. Изложим его вкратце. (См.)
Рассмотрим множество  всех бесконечных последовательностей всех бесконечных последовательностей
 , ,  , ,  , ,  , ,  , ,
у которых все  , кроме конечного числа, равны нулю. Для , кроме конечного числа, равны нулю. Для  , ,  , ,  , ,  и и
 , , 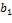 , ,  , , 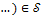 определим сумму определим сумму  и произведение и произведение  , полагая , полагая
 , , 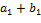 , , 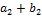 , ,  , ,
 , ,  , ,  , ,  , ,
где

Относительно этих операций  является коммутативным кольцом с единицей является коммутативным кольцом с единицей
 , ,  , ,  , ,  . Действительно, сложение и умножение двух последовательностей с конечным числом ненулевых членов даёт снова аналогичную последовательность. Сложение последовательностей ассоциативно и коммутативно. Нулём в . Действительно, сложение и умножение двух последовательностей с конечным числом ненулевых членов даёт снова аналогичную последовательность. Сложение последовательностей ассоциативно и коммутативно. Нулём в  является нулевая последовательность является нулевая последовательность  , ,  , ,  , ,  , противоположным для , противоположным для  , ,  , ,  , ,  является элемент является элемент  = =
( , ,  , ,  , ,  . Умножение в . Умножение в  ассоциативно: пусть ассоциативно: пусть
 , ,  , ,  , ,  , ,  , , 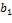 , ,  , ,  , ,  , ,  , ,  , …) , …)
− три произвольных элемента из  ; тогда ; тогда
 = ( = (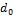 , ,  , ,  , …), , …),  = ( = ( , ,  , ,  , …), , …),
где

Вычисление  даёт тот же результат. Поскольку умножение в исходном кольце даёт тот же результат. Поскольку умножение в исходном кольце  коммутативно, то оно коммутативно и в коммутативно, то оно коммутативно и в  . Наконец, в . Наконец, в  выполняется дистрибутивный закон: выполняется дистрибутивный закон:  . Значит, . Значит,  коммутативное кольцо с единицей. коммутативное кольцо с единицей.
Множество  последовательностей ( последовательностей ( , ,  , ,  , ,  , у которых лишь первая компонента может быть ненулевой, образует в , у которых лишь первая компонента может быть ненулевой, образует в  подкольцо, изоморфное подкольцо, изоморфное  (изоморфизм задаётся соответствием (изоморфизм задаётся соответствием  , ,  , ,  , , 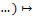  . Отождествляя . Отождествляя  и и  , можно считать, что , можно считать, что  − подкольцо в − подкольцо в  , а , а  – расширение кольца – расширение кольца  . Обозначим через . Обозначим через 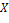 последовательность ( последовательность ( , ,  , ,  , ,  , ,  и назовём и назовём 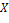 переменной (или неизвестной) над переменной (или неизвестной) над  . Легко проверить, что . Легко проверить, что
 ,…, ,…,  , ,  , ,  , ,  для всех для всех  , ,
где  является является 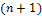 -ой компонентой. Если, кроме того, положить -ой компонентой. Если, кроме того, положить 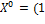 , ,  , ,  , ,  , то для любой последовательности , то для любой последовательности  , ,  , ,  , ,  имеем: имеем:  , ,  , ,  , , 
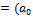 , ,  , ,  , , 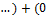 , ,  , ,  , , 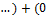 , ,  , ,  , 0, , 0, 
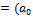 , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , , 
 , ,  , ,  , ,  , ,  , ,  , ,   , ,  , ,  , , 

Таким образом, если  − последний ненулевой элемент в − последний ненулевой элемент в  , ,  , ,  , ,  , ,  , ,  , то в новых обозначениях , то в новых обозначениях

Такое представление  единственно. Действительно, если допустить, что единственно. Действительно, если допустить, что

− другое представление  , то , то  , ,  , ,  , , 
 , , 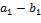 , ,  , , 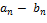 , ,  , ,  , ,  , ,
откуда следует, что  ,…, ,…, 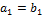 , ,  . .
Определение. Введённое кольцо  обозначается через обозначается через  и называется кольцом многочленов над и называется кольцом многочленов над  от одной переменной от одной переменной 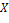 , а его элементы − многочленами (или поли , а его элементы − многочленами (или поли
|



 − идеал кольца
− идеал кольца  . Поскольку каждый идеал кольца является нормальной подгруппой аддитивной группы кольца, то идеал
. Поскольку каждый идеал кольца является нормальной подгруппой аддитивной группы кольца, то идеал 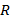 по модулю идеала
по модулю идеала  . Класс вычетов, содержащий элемент
. Класс вычетов, содержащий элемент  , будем обозначать через
, будем обозначать через  =
=  ; он состоит из элементов вида
; он состоит из элементов вида  ,
, 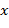 ∈
∈  ⟺
⟺  .
. . Тогда
. Тогда  и
и  .
. и
и  для некоторых
для некоторых  ,
,  . Тогда
. Тогда )−(
)−( =
= 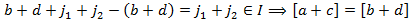 ;
; ∎
∎ ,
,  .
. .
. ,
, 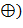 абелева. Операция умножения ассоциативна:
абелева. Операция умножения ассоциативна: .
. ,
, . ∎
. ∎ ,
,  , принадлежащие одному и тому же классу вычетов по модулю идеала
, принадлежащие одному и тому же классу вычетов по модулю идеала  . Отметим следующие свойства определённого сравнения: если
. Отметим следующие свойства определённого сравнения: если 
 , то
, то ,
,  ,
, 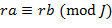 и
и 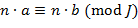
 и
и 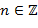 ; если, кроме того,
; если, кроме того,  , то
, то  и
и 
 , +,
, +,  − кольцо целых чисел,
− кольцо целых чисел, ,
,  ,
,  , где
, где 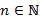 , − идеал (главный) в кольце
, − идеал (главный) в кольце  , состоящий из чисел, кратных
, состоящий из чисел, кратных  . Элементами кольца
. Элементами кольца  ,
,  ,
,  являются те же смежные классы, что и в примере с операциями:
являются те же смежные классы, что и в примере с операциями: 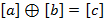 ,
,  , где
, где 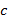 и
и  − остатки от деления соответственно
− остатки от деления соответственно 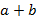 и
и  на
на  .
. .
.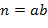 для некоторых целых
для некоторых целых  ,
,  . Тогда
. Тогда  , откуда следует, что
, откуда следует, что  − простое число. Пусть
− простое число. Пусть  – любой ненулевой элемент. Так как
– любой ненулевой элемент. Так как  при
при  , то элементы
, то элементы  ,
, 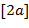 , …,
, …,  различны и совпадают с элементами
различны и совпадают с элементами  ,
,  , …,
, …,  (но, возможно, в другом порядке), то
(но, возможно, в другом порядке), то ].
]. . Так как числа
. Так как числа  ,
,  , …,
, …,  ) взаимно просты с
) взаимно просты с 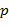 , то обе части полученного сравнения можно сократить на эти числа. В результате получаем
, то обе части полученного сравнения можно сократить на эти числа. В результате получаем ,
, имеет обратный. Значит,
имеет обратный. Значит, 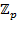 − поле. ∎
− поле. ∎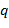 элементов, будем обозначать через
элементов, будем обозначать через  (используют также обозначение
(используют также обозначение 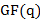 – от
– от  − поле Галуа − по имени фр. математика Э. Галуа, заложившего фундаментальные основы теории групп). В частности,
− поле Галуа − по имени фр. математика Э. Галуа, заложившего фундаментальные основы теории групп). В частности,  , если
, если  и
и  , как кольца с делителями нуля, не являются полями. Вместе с тем поле
, как кольца с делителями нуля, не являются полями. Вместе с тем поле  существует, а поле
существует, а поле  не существует. Далее будет установлено, при каких
не существует. Далее будет установлено, при каких  существует поле
существует поле 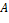 ,
, 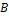 −
−  . Тогда:
. Тогда: − сюръективный гомоморфизм, то
− сюръективный гомоморфизм, то  − идеал в
− идеал в  .
.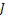 − идеал в
− идеал в  , определяемое по правилу
, определяемое по правилу  , является сюръективным гомоморфизмом с ядром
, является сюръективным гомоморфизмом с ядром  .
. называют естественным, или каноническим.
называют естественным, или каноническим. и
и  , сопоставляющего классу вычетов
, сопоставляющего классу вычетов  элемент
элемент 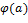 . Отображение
. Отображение  тот же класс вычетов. что и
тот же класс вычетов. что и  , то
, то  для некоторого
для некоторого  и
и ,
, определено однозначно. Далее, если
определено однозначно. Далее, если  , то
, то  , поскольку в противном случае приходим к противоречию:
, поскольку в противном случае приходим к противоречию: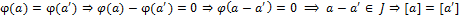 .
. сюръекция, т.е.
сюръекция, т.е.  , то для любого
, то для любого  найдётся
найдётся 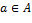 такой, что
такой, что  . Отсюда следует, что и
. Отсюда следует, что и  имеем
имеем
 .
. ,
,  имеем
имеем
 .
. и
и  ,
, для любого
для любого  . Если такое
. Если такое  при любом
при любом  ; если же существуют
; если же существуют  , то Char
, то Char  , где
, где  − наименьшее из таких
− наименьшее из таких  = 0.
= 0. . Так как
. Так как 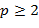 . Допустим на минутку, что
. Допустим на минутку, что  − составное число, т.е.
− составное число, т.е.  ,где
,где  ,
,  − некоторые целые. Тогда из
− некоторые целые. Тогда из 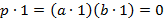 следует, что или
следует, что или  , или
, или  (либо и то, и другое). Пусть, для определённости,
(либо и то, и другое). Пусть, для определённости,  , что противоречит выбору числа
, что противоречит выбору числа  имеет место тождество
имеет место тождество для всех
для всех  и
и  для любых
для любых  . Тогда
. Тогда
 , а из него вытекает второе:
, а из него вытекает второе:  . ∎
. ∎ для всех
для всех  ,…,
,…,  и
и  ,
,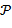 поля
поля  называется подкольцо в
называется подкольцо в  − поле рациональных чисел − является подполем поля
− поле рациональных чисел − является подполем поля  вещественных чисел, которое, в свою очередь, является подполем поля
вещественных чисел, которое, в свою очередь, является подполем поля  комплексных чисел.
комплексных чисел. , то говорят, что поле
, то говорят, что поле  (или надполем по отношению к
(или надполем по отношению к  и
и  поля
поля  ∩
∩ 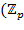 ,
,  имеет простой порядок и по теореме Лагранжа не имеет собственных подгрупп. 2)
имеет простой порядок и по теореме Лагранжа не имеет собственных подгрупп. 2)  , причём
, причём  , если Char
, если Char  , и
, и  , если Char
, если Char  .
. и
и  поля
поля  , мы неизбежно придём к противоречию, поскольку их пересечение
, мы неизбежно придём к противоречию, поскольку их пересечение  содержится как в
содержится как в 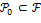 единственно.
единственно. . Это поле, как всякое подполе поля
. Это поле, как всякое подполе поля  поля
поля 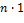 ,
,  , с операциями
, с операциями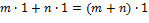 ,
, 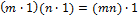 ,
,  ,
,  ,
, . Это отображение является сюръективным гомоморфизмом кольца
. Это отображение является сюръективным гомоморфизмом кольца  на кольцо
на кольцо  . По теореме о гомоморфизмах колец
. По теореме о гомоморфизмах колец  . Возможны два случая:
. Возможны два случая:
 . В этом случае ядро тривиально, т.е. Ker
. В этом случае ядро тривиально, т.е. Ker 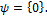 Следовательно,
Следовательно,  ) и дроби
) и дроби  , имеющие смысл в
, имеющие смысл в 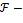 поле), образуют поле, изоморфное ℚ. Оно и будет простым подполем в
поле), образуют поле, изоморфное ℚ. Оно и будет простым подполем в  . Поскольку
. Поскольку  Char
Char  − поле. Так что
− поле. Так что  ≅
≅  − поле. Поскольку
− поле. Поскольку  , то на самом деле
, то на самом деле  . ∎
. ∎ − коммутативное кольцо с единицей
− коммутативное кольцо с единицей 
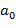 , …,
, …,  − элементы кольца
− элементы кольца  ,
,  − некоторый (формальный) символ, не принадлежащий кольцу
− некоторый (формальный) символ, не принадлежащий кольцу  и посторонней переменной
и посторонней переменной  . Этого вопроса обычно избегают. Однако можно дать совершенно безукоризненное определение многочлена как элемента кольца многочленов. Изложим его вкратце. (См.)
. Этого вопроса обычно избегают. Однако можно дать совершенно безукоризненное определение многочлена как элемента кольца многочленов. Изложим его вкратце. (См.) всех бесконечных последовательностей
всех бесконечных последовательностей ,
,  ,
,  ,
,  ,
,  ,
, ,
,  ,
, 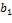 ,
,  ,
, 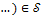 определим сумму
определим сумму  и произведение
и произведение  , полагая
, полагая ,
, 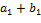 ,
, 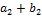 ,
,  ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
,  =
= ,
,  ,
,  ,
,  ,
, 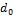 ,
,  ,
,  , …),
, …),  = (
= ( ,
,  ,
,  , …),
, …),
 даёт тот же результат. Поскольку умножение в исходном кольце
даёт тот же результат. Поскольку умножение в исходном кольце  коммутативно, то оно коммутативно и в
коммутативно, то оно коммутативно и в  . Наконец, в
. Наконец, в  . Значит,
. Значит,  последовательностей (
последовательностей ( ,
,  ,
, 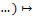
 . Отождествляя
. Отождествляя 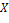 последовательность (
последовательность ( ,
,  ,…,
,…,  ,
,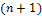 -ой компонентой. Если, кроме того, положить
-ой компонентой. Если, кроме того, положить 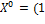 ,
,  , то для любой последовательности
, то для любой последовательности  имеем:
имеем: 
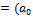 ,
, 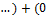 ,
, 
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
 ,
, 

 − последний ненулевой элемент в
− последний ненулевой элемент в  ,
, 
 единственно. Действительно, если допустить, что
единственно. Действительно, если допустить, что
 ,
,  ,
, 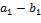 ,
, 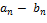 ,
,  ,…,
,…, 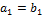 ,
,  .
. и называется кольцом многочленов над
и называется кольцом многочленов над 


