
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяционная формула НьютонаСодержание книги
Поиск на нашем сайте Пусть Теорема. Пусть (1) Доказательство. Существование. Если (2) ( (3) Подставляя (3) в (2), получим искомое разложение (1). Единственность. Допустим, что существуют два разложения, удовлетворяющие условиям теоремы:
Тогда
Очевидно, что Следствие. Пусть
Если
Определение. Для многочлена
определим его гиперпроизводную порядка Стандартное соглашение о биномиальных коэффициентах, согласно которому Гиперпроизводные обладают свойством линейности относительно поля
для всех Лемма.
Доказательство. Имеем
Теорема. Для любого элемента
называемое разложением в ряд Тейлора. Доказательство. Для многочлена откуда следует, что Следствие. Элемент
Доказательство. Если Замечание. Идея использовать гиперпроизводные для исследования функций над поля ненулевой характеристики принадлежит Хассе (1936), а также Тайхмюллеру, который исследовал основные свойства гиперпроизводных. (См.) Обычные производные Следствие. Пусть
|
||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.112.65 (0.008 с.) |

 − поле.
− поле. ,…,
,…,  − любые (необязательно различные) многочлены со степенями
− любые (необязательно различные) многочлены со степенями  . Тогда для любого многочлена
. Тогда для любого многочлена  , степень которого не превосходит
, степень которого не превосходит  , существуют однозначно определённые многочлены
, существуют однозначно определённые многочлены  ,…,
,…,  такие, что deg
такие, что deg 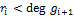 ,
,  , и
, и .
. , то возьмём
, то возьмём  и
и  для
для  . Предположим, что
. Предположим, что  . Представим
. Представим  в виде
в виде ,
, 
 − частное от деления
− частное от деления  , то по предположению индукции существуют многочлены
, то по предположению индукции существуют многочлены  ,…,
,…, 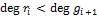 ,
,  , и
, и .
. .
. .
. , а так как
, а так как  , то
, то 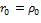 . Разделив наше равенство на
. Разделив наше равенство на  . Продолжая этот процесс, получим
. Продолжая этот процесс, получим  ,…,
,…, 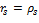 . Это доказывает единственность разложения (1). ∎
. Это доказывает единственность разложения (1). ∎ ,…,
,…,  − любые элементы. Тогда любой многочлен
− любые элементы. Тогда любой многочлен  представим в виде
представим в виде для однозначно определяемых констант
для однозначно определяемых констант  ,…,
,…,  .
.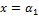 ,…,
,…,  . Представление (1), где
. Представление (1), где  называется
называется  - адическим разложением многочлена
- адическим разложением многочлена  -адическое разложение совпадает с обычной записью многочлена
-адическое разложение совпадает с обычной записью многочлена  ,
,  , уточняя значения коэффициентов
, уточняя значения коэффициентов  в разложении
в разложении
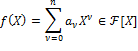
 (кратко:
(кратко: 
 при
при 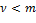 , гарантирует, что
, гарантирует, что 
 ,
,  и
и  .
. ,
,  ,
,  ,
, 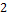 ,…
,…


 имеет место следующее разложение:
имеет место следующее разложение:

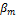 =
=  ,
,  [
[ 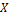 ] тогда и только тогда, когда
] тогда и только тогда, когда для
для 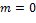 ,
,  , но
, но  .
. −
− 
 ,
,  -кратным корнем.∎
-кратным корнем.∎ и гиперпроизводные
и гиперпроизводные  связаны соотношением:
связаны соотношением:  , которое имеет место, если Char
, которое имеет место, если Char  или
или  , но при этом
, но при этом  . Для данного случая следствие можно сформулировать так:
. Для данного случая следствие можно сформулировать так: − неотрицательное целое число, причём любое, если
− неотрицательное целое число, причём любое, если  , и
, и  , если
, если  . Элемент
. Элемент 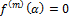 для
для  .
.


