
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корни многочлена. Теорема БезуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если Если Если будем делить многочлен Теорема Безу. Элемент многочлена
Для деления многочлена Пусть
и пусть
где Сравнивая коэффициенты при одинаковых степенях Теорема.Пусть несократимая дробь Из данной теоремы вытекает, что решение вопроса о наличии рациональных корней многочлена сводится к следующим действиям: 1. перебору всех делителей свободного члена и всех делителей старшего члена; 2. составлению из них несократимых дробей; 3. проверке посредством подстановки дроби в многочлен. На этом этапе можно воспользоваться методом Горнера. Если все испытания приведут к отрицательному результату, то это значит, что у многочлена нет рациональных корней. Теорема (о границе вещественных корней многочлена с вещественными коэффициентами). Пусть
Упорядоченная последовательность не равных нулю многочленов 1) 2) соседние многочлены ряда не обращаются в нуль при одном и том же значении 3) если 4) произведение Последовательность Штурма позволяет определять количество действительных корней многочлена
Теорема (Штурма). Пусть Элементы теории чисел Сравнения. Свойства сравнений Следует сразу отметить, что в дальнейшем речь пойдет о кольце Говорят, что число Два целых числа Отношение сравнимости по модулю Опишем простейшие свойства сравнений. Многие свойства сравнений аналогичны свойствам равенств. Свойство 1. Сравнения можно почленно складывать и вычитать, то есть если Свойство 2. Сравнения можно почленно перемножить, то есть если Свойство 3. Обе части сравнения можно разделить на их общий множитель, если он взаимно простой с модулем. Если Свойство 4. Обе части сравнения и модуль можно разделить на их общий делитель. Если Следствие 5. Пусть Теорема Вильсона. Если Функция Эйлера Количество положительных целых чисел, не превосходящих n и взаимно простых с n, обозначается через Теорема. 1) Если 2) Если 3) Если В теории сравнений важную роль играют теоремы Эйлера и Ферма. Теорема Эйлера. Если целое число а взаимно просто с m, то Теорема Ферма. Если целое число а не делится на простое число Сравнения первой степени Сравнением первой степени называют сравнение вида Решить сравнение значит найти все целочисленные значения
Сформулируем условия разрешимости сравнения первой степени. Теорема. Если Н.О.Д. Теорема. Пусть Н.О.Д. Теорема (китайская теорема об остатках). Пусть Сравнение высших степеней Перейдем к рассмотрению вопроса о числе решений сравнения Сравнение вида Теорема. Сравнение Теорема. Пусть Цепные дроби Пусть Применим алгоритм Евклида к числам
|
||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 875; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.1.100 (0.01 с.) |

 - некоторый многочлен, а
- некоторый многочлен, а  некоторое число, то число
некоторое число, то число  полученное заменой неизвестного
полученное заменой неизвестного  числом
числом  и последующим выполнением всех указанных операций, называется значением многочлена
и последующим выполнением всех указанных операций, называется значением многочлена  при
при  .
. то есть многочлен
то есть многочлен  является корнем
является корнем тогда и только тогда, когда
тогда и только тогда, когда  .
. существует метод, называемый схемой Горнера.
существует метод, называемый схемой Горнера.





 Таким образом, коэффициенты частного и остаток можно последовательно получать при помощи однотипных вычислений, по формулам, называемым схемой Горнера.
Таким образом, коэффициенты частного и остаток можно последовательно получать при помощи однотипных вычислений, по формулам, называемым схемой Горнера. является корнем многочлена
является корнем многочлена  с целыми коэффициентами. Тогда
с целыми коэффициентами. Тогда  и
и  .
. ,
, ,
,  первый отрицательный коэффициент в последовательности
первый отрицательный коэффициент в последовательности  коэффициентов.
коэффициентов.  - наибольший модуль отрицательных коэффициентов, тогда все корни многочлена
- наибольший модуль отрицательных коэффициентов, тогда все корни многочлена  меньше числа
меньше числа 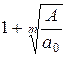 (в случае
(в случае  меньше
меньше  ).
).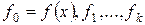 называется последовательностью Штурма (рядом Штурма) для многочлена
называется последовательностью Штурма (рядом Штурма) для многочлена  на
на  , если выполняются следующие условия:
, если выполняются следующие условия:
 ;
; , то
, то 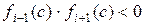 для любого
для любого  ;
; меняет знак с минуса на плюс, когда
меняет знак с минуса на плюс, когда  . Обозначим
. Обозначим  - количество перемен знака в последовательности чисел:
- количество перемен знака в последовательности чисел: 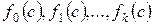 .
.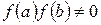 , тогда количество вещественных корней многочлена
, тогда количество вещественных корней многочлена  .
. целых чисел.
целых чисел. делит число
делит число  (обозначается
(обозначается 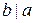 ) или
) или  .
. , где
, где  , если
, если  . Обозначают
. Обозначают  .
.
 , то
, то 
 и число
и число  , то
, то 
 есть любой делитель числа
есть любой делитель числа  , то
, то 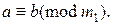
 – простое число, то
– простое число, то 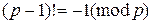 .
. ; числовая функция
; числовая функция 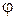 , определенная на множестве всех целых положительных чисел, называется функцией Эйлера. Легко видеть, что функция
, определенная на множестве всех целых положительных чисел, называется функцией Эйлера. Легко видеть, что функция  - простое число, то
- простое число, то  ;
;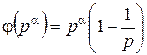 ;
; - каноническое разложение натурального числа
- каноническое разложение натурального числа  ; то
; то 
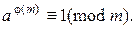

 , где
, где  ,
,  то сравнение
то сравнение  имеет одно и только одно решение по модулю
имеет одно и только одно решение по модулю  Сравнение
Сравнение  разрешимо тогда и только тогда, когда
разрешимо тогда и только тогда, когда  Если
Если  , то сравнение имеет своими решениями точно
, то сравнение имеет своими решениями точно  классов вычетов по модулю
классов вычетов по модулю 
 - попарно взаимно простые числа, и пусть
- попарно взаимно простые числа, и пусть  - целые числа. Тогда существует единственное по модулю
- целые числа. Тогда существует единственное по модулю 
 й степени.
й степени. называют сравнением высшего порядка.
называют сравнением высшего порядка. степени
степени  , Н.О.Д.
, Н.О.Д. 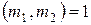 , тогда сравнение
, тогда сравнение  равносильно системе сравнений
равносильно системе сравнений 
 - рациональное число:
- рациональное число:  Число
Число 
 (
( - «частное»,
- «частное»,  - «остаток»), для которых
- «остаток»), для которых  , где
, где 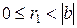 . То в свою очередь для чисел
. То в свою очередь для чисел 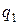 и
и  такие, что
такие, что  , где
, где  . Далее
. Далее  и
и  такие, что
такие, что 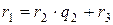 , где
, где  и так далее до тех пор пока остаток
и так далее до тех пор пока остаток 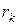 не станет равен нулю. Тогда
не станет равен нулю. Тогда 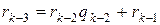 ;
;  .
. и
и  (3.1)
(3.1)


