
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бинарная операция. Формы записи. ГруппаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Элементы теории групп Бинарная операция. Формы записи. Группа Важнейшим типом алгебраических систем с одной операцией являются группы. Это понятие обладает чрезвычайно широкой областью применений и служит предметом большой самостоятельной науки – теории групп. Введем основные понятия, использующиеся в теории групп. Пусть Х - непустое множество. Бинарной операцией, определенной над Х, называется отображение Как правило, для обозначения бинарной операции Непустое множество Х с бинарной операцией *, введенной Бинарная операция Элемент Элемент Определение. Алгебраическая структура 1) Бинарная операция 2) В ней существует нейтральный (единичный) элемент 3) Для каждого элемента Подмножество Порядком элемента Если такого числа не существует, то говорят, что порядок элемента Гомоморфизм и изоморфизм групп Пусть Ядром гомоморфизма Образом гомоморфизма Определим, какая запись называется мультипликативной, а какая – аддитивной. При мультипликативной записи бинарную операцию называют умножением и пишут При аддитивной записи бинарную операцию называют сложением чисел, унарную операцию называют операцией перехода к противоположному элементу, нейтральный элемент называют нулем группы и обозначают 0. Следует помнить, что противопоставление “аддитивные группы – мультипликативные группы” не относятся к противопоставлению самих понятий, а лишь к условным обозначениям. При трактовке абелевых групп в основном пользуются аддитивной записью, при изложении положений, относящихся к произвольным группам, - общепринятой мультипликативной системой обозначения. Перечислим свойства гомоморфизма групп: 1) 2) 3) Если гомоморфизм групп является взаимнооднозначным, то он называется изоморфизмом, а группы изоморфными. Фактор-группа Множество Стоит заметить, что если Множество смежных классов элементов группы На множестве Теорема(об изоморфизме). Гомоморфный образ группы изоморфен фактор-группе по ядру гомоморфизма (
Идеалы колец Подгруппа Пусть К – кольцо, 1) 2) Фактор-кольцо Элементы теории чисел Функция Эйлера Количество положительных целых чисел, не превосходящих n и взаимно простых с n, обозначается через Теорема. 1) Если 2) Если 3) Если В теории сравнений важную роль играют теоремы Эйлера и Ферма. Теорема Эйлера. Если целое число а взаимно просто с m, то Теорема Ферма. Если целое число а не делится на простое число Сравнения первой степени Сравнением первой степени называют сравнение вида Решить сравнение значит найти все целочисленные значения Сформулируем условия разрешимости сравнения первой степени. Теорема. Если Н.О.Д. Теорема. Пусть Н.О.Д. Теорема (китайская теорема об остатках). Пусть Сравнение высших степеней Перейдем к рассмотрению вопроса о числе решений сравнения Сравнение вида Теорема. Сравнение Теорема. Пусть Цепные дроби Пусть Применим алгоритм Евклида к числам
Примеры решения задач Задача №1 Выяснить, образует ли группу множество
всех линейных отображений числовой прямой на себя, относительно операции композиции отображения. Решение: Для того, чтобы множество
Проверим выполнимость вышеуказанных аксиом для множества
тогда
так как
Таким образом, нулевая аксиома выполняется. Далее, пусть
Отображения Рассмотрим элемент Проверим выполнимость четвёртой аксиомы. Для этого рассмотрим
Если Таким образом, если Если же Итак, не для всякого элемента множество Заметим, что если обозначить Задача №2 Доказать, что фактор-группа мультипликативной группы Решение: Для того, чтобы доказать требуемое, воспользуемся теоремой об изоморфизме, (см. п. 1.3). Рассмотрим отображение Так как Задача №3 Найти порядок элемента Решение: Для того, чтобы найти порядок комплексного числа Ответ: 4 Задача №4 Пусть Решение: Для того, чтобы решить уравнение
то обратная перестановка
поэтому
Для того чтобы найти порядок перестановки Чётность перестановки можно определить по количеству инверсий в ней (см. п. 1.4.). Последнее определяется как количество таких пар элементов второй строки, в которых первым стоит число большее, нежели второе. Рассмотрим перестановку
Начнём с элемента 2, который стоит первым во второй строке. Он образует следующие пары: (24), (25), (26), (21) и (23), из которых лишь пара (21) образует инверсию. Далее элемент 4 и его пары: (45), (46), (41), (43). Инверсии образуют две пары (41) и (43). Элемент 5 образует инверсии с элементами 1 и 3. То же самое можно сказать и про элемент 6. Предпоследний элемент 1 образует лишь одну пару (13), но она инверсию не образует. Последний элемент 3 пар не образует (точнее его пары уже все рассматривались). Итак, количество инверсий перестановки Задача №5 Выяснить, является ли множество Решение: Для того чтобы множество
Кроме этого, если
Если же в коммутативном кольце Итак, нужно проверить выполняются ли все вышеуказанные аксиомы. Пусть
так как Аналогично
Для того чтобы убедиться, что верна и вторая часть рассматриваемой аксиомы, отдельно раскроем значения выражений Итак
Далее в качестве нулевого элемента рассмотрим
Аксиома (4) следует из свойств коммутативности для действительных чисел:
Теперь свойство дистрибутивности:
Аналогично проверяется справедливость 2-го свойства дистрибутивности Из всего вышесказанного следует, что множество A является коммутативным кольцом с единичным элементом
Далее для элемента
Тогда
Откуда
если Итак, Задача №6 Является ли идеалом множество Решение: Проверим, образует ли множество
2) так как 3) если
Из свойств 0) - 4) следует, что J является коммутативной группой по сложению. Заметим при этом, что аксиомы 1) – 4) можно было не проверять, так как они справедливы для всех элементов любого кольца в том числе и для тех его элементов, которые входят в J. Достаточно было бы проверить, что нулевой элемент кольца Теперь рассмотрим произведение Итак
Следовательно, J является лишь правым идеалом кольца Задача №7 Разложить многочлен
Решение: Согласно свойствам делимости в кольце
такой, что
В данном случае
или Далее разделим многочлен то есть
Тогда искомое разложение можно получить путём ещё 4-х кратного применения схемы Горнера. Все это можно оформить в виде таблицы – схемы.
Откуда
С другой стороны многочлен
Сравнивая коэффициенты при одинаковых степенях скобки,
Задача №8 Разложить на неприводимые множители многочлен Решение: Поиск разложения следует начать с поиска корней данного многочлена. На основании теоремы о рациональных корнях многочлена с целыми коэффициентами целочисленные корни следует искать среди делителей свободного коэффициента (см. 2.4.). В данном случае – среди делителей числа 6, то есть в множестве Деление многочлена
Откуда
Где многочлен
Раскроем скобки и приравняем коэффициенты при одинаковых степенях x:
Получается система
Одним из решений которой является следующий набор переменных: A=-2; B=2; C=1; D=-3. Тогда
Так как многочлены
Откуда разложение
а над C [ x ]
Задача №9 С помощью ряда Штурма изолировать корни многочлена Решение: Сначала найдём границы корней данного многочлена (см. 2.4.). На основании теоремы о границе вещественных корней многочлена
тогда корни многочлена | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


 вместо
вместо  пишут
пишут  , при этом используют какой-нибудь специальный символ:
, при этом используют какой-нибудь специальный символ:  .
. на этом множестве, называется алгебраической структурой
на этом множестве, называется алгебраической структурой 
 для всех
для всех  ; она называется коммутативной, если
; она называется коммутативной, если 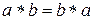 . Те же названия присваиваются и соответствующей алгебраической структуре
. Те же названия присваиваются и соответствующей алгебраической структуре  .
. называется единичным (или нейтральным) относительно рассматриваемой бинарной операции *, если
называется единичным (или нейтральным) относительно рассматриваемой бинарной операции *, если 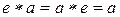 для всех
для всех  .
. называется обратным к элементу
называется обратным к элементу  .
. называется группой, если
называется группой, если ;
; существует обратный
существует обратный  .
. называется подгруппой в
называется подгруппой в  , если
, если  ;
;  и
и  .
.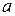 группы
группы  такое, что
такое, что  , где
, где  (или
(или  ).
). две группы. Отображение
две группы. Отображение  называется гомоморфизмом, если
называется гомоморфизмом, если 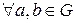
 .
.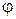 называется множество
называется множество  , где
, где  - единица группы
- единица группы  .
. .
. или
или 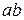 вместо
вместо  , унитарную операцию называют операцией перехода к обратному элементу и обозначают a
, унитарную операцию называют операцией перехода к обратному элементу и обозначают a  , нейтральный элемент называют единицей группы и обозначают
, нейтральный элемент называют единицей группы и обозначают 
 ;
;
 , где
, где  - подгруппа группы
- подгруппа группы  . Если подгруппа
. Если подгруппа  ), то она называется нормальной подгруппой группы
), то она называется нормальной подгруппой группы 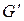 , то
, то  нормальная подгруппа
нормальная подгруппа  подгруппа
подгруппа  (
( ).
). . Тогда
. Тогда  является группой, называемой фактор-группой группы
является группой, называемой фактор-группой группы  ).
).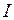 аддитивной группы (К,+) кольца К называется левым (правым) идеалом, если
аддитивной группы (К,+) кольца К называется левым (правым) идеалом, если  и
и 
 . Если идеал
. Если идеал  , целых чисел делящихся на
, целых чисел делящихся на  , в кольце целых чисел
, в кольце целых чисел  .
. - двусторонний идеал. Для любого элемента
- двусторонний идеал. Для любого элемента  множество
множество  называется его классом смежности. Множество классов смежности элементов кольца К относительно идеала
называется его классом смежности. Множество классов смежности элементов кольца К относительно идеала  .
. 
 .
. обозначают
обозначают  . Оно состоит из
. Оно состоит из 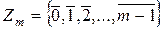 и является полем тогда и только тогда, когда
и является полем тогда и только тогда, когда 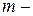 простое число.
простое число. ; числовая функция
; числовая функция  - простое число, то
- простое число, то  ;
;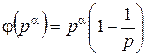 ;
; - каноническое разложение натурального числа
- каноническое разложение натурального числа 
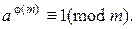

 , где
, где  ,
,  - переменная.
- переменная. то сравнение
то сравнение  имеет одно и только одно решение по модулю
имеет одно и только одно решение по модулю  Сравнение
Сравнение  разрешимо тогда и только тогда, когда
разрешимо тогда и только тогда, когда  Если
Если  , то сравнение имеет своими решениями точно
, то сравнение имеет своими решениями точно  классов вычетов по модулю
классов вычетов по модулю 
 - попарно взаимно простые числа, и пусть
- попарно взаимно простые числа, и пусть  - целые числа. Тогда существует единственное по модулю
- целые числа. Тогда существует единственное по модулю 
 й степени.
й степени. называют сравнением высшего порядка.
называют сравнением высшего порядка. степени
степени  , Н.О.Д.
, Н.О.Д. 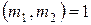 , тогда сравнение
, тогда сравнение  равносильно системе сравнений
равносильно системе сравнений 
 - рациональное число:
- рациональное число:  Число
Число 
 (
( - «частное»,
- «частное»,  - «остаток»), для которых
- «остаток»), для которых  , где
, где 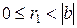 . То в свою очередь для чисел
. То в свою очередь для чисел  и
и 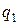 и
и  такие, что
такие, что  , где
, где  . Далее
. Далее  и
и  такие, что
такие, что 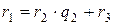 , где
, где  и так далее до тех пор пока остаток
и так далее до тех пор пока остаток 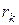 не станет равен нулю. Тогда
не станет равен нулю. Тогда 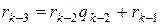 ;
;  .
. и
и  (3.1)
(3.1)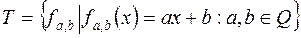
 являлось группой, необходимо и достаточно, чтобы на множестве его элементов было определено бинарная операция «
являлось группой, необходимо и достаточно, чтобы на множестве его элементов было определено бинарная операция «
 ,
,
 ,если
,если 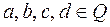 .
. тогда:
тогда:
 .
. и
и 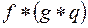 равны.
равны. . Тогда, если
. Тогда, если 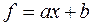 , то
, то  , аналогично
, аналогично  . Следовательно, в множестве
. Следовательно, в множестве  .
. , обозначим
, обозначим  , тогда
, тогда .
. , то
, то  . То есть
. То есть  . Так как
. Так как  , то
, то  если
если  .
. , то для
, то для 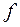 существует
существует  - обратный элемент.
- обратный элемент. , то есть
, то есть  , то для такого элемента
, то для такого элемента 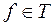 обратный элемент не существует.
обратный элемент не существует. множество элементов
множество элементов  с
с  , то
, то  образует группу относительно операции композиции отображений.
образует группу относительно операции композиции отображений. невырожденных рациональных матриц порядка
невырожденных рациональных матриц порядка  по подгруппе
по подгруппе  матриц с определителем, равным 1, изоморфна мультипликативной группе
матриц с определителем, равным 1, изоморфна мультипликативной группе  рациональных чисел, отличных от нуля.
рациональных чисел, отличных от нуля. , определённое следующим образом:
, определённое следующим образом: 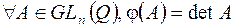 .
. , следовательно
, следовательно  гомоморфизм групп, при этом его образ
гомоморфизм групп, при этом его образ  , а ядро
, а ядро  . На основании теоремы следует, что
. На основании теоремы следует, что  , то есть
, то есть 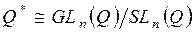 , что и требовалось доказать.
, что и требовалось доказать. мультипликативной группы
мультипликативной группы 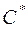 комплексных чисел без нуля.
комплексных чисел без нуля. (см. п. 1.1), нужно найти
(см. п. 1.1), нужно найти  . Итак,
. Итак, 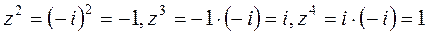 . Так как 1 является единичным элементом в группе
. Так как 1 является единичным элементом в группе  .
. . Решить уравнение
. Решить уравнение  . Найти порядок перестановки
. Найти порядок перестановки  . Определить чётность перестановки
. Определить чётность перестановки  .
. обратную к
обратную к  . Если перестановка
. Если перестановка 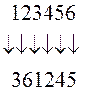 ,
, или
или 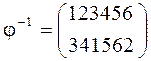 ,
, .
. . Следовательно,
. Следовательно,  .
. .
. . Число 7 является нечётным, следовательно, и перестановка
. Число 7 является нечётным, следовательно, и перестановка  кольцом (полем) относительно операций
кольцом (полем) относительно операций  и
и  .
.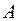 являлось кольцом относительно операций сложения
являлось кольцом относительно операций сложения  и умножения
и умножения 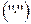 необходимо и достаточно выполнения следующих аксиом (см. 2.1.):
необходимо и достаточно выполнения следующих аксиом (см. 2.1.):
 , то кольцо называется коммутативным если
, то кольцо называется коммутативным если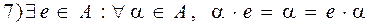 , то кольцо называется кольцом с единичным элементом.
, то кольцо называется кольцом с единичным элементом.
 , то
, то  тогда
тогда ,
,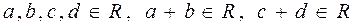 .
.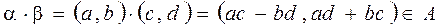 . Далее рассмотрим
. Далее рассмотрим
 и
и  .
.
 . Пусть
. Пусть  , то
, то  и наоборот
и наоборот  . Если
. Если  , то обратным к нему элементом является элемент, который можно обозначить
, то обратным к нему элементом является элемент, который можно обозначить  , так как
, так как

 .
.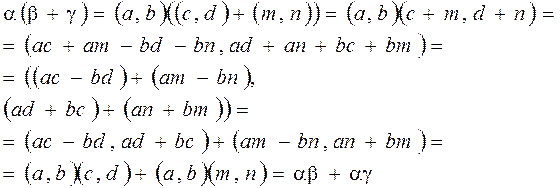
 .
. , так как
, так как
 найдём обратный элемент
найдём обратный элемент 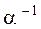 . Его «координаты» обозначим
. Его «координаты» обозначим  . Следовательно, должно выполняться равенство:
. Следовательно, должно выполняться равенство:  или
или  , то есть
, то есть .
. .
. ,
, .
. такой, что
такой, что  . Следовательно, A является полем.
. Следовательно, A является полем. в кольце
в кольце 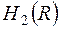 вещественных матриц
вещественных матриц  ?
? согласно определению (см. п. 2.3). Итак:
согласно определению (см. п. 2.3). Итак:
 - нулевой элемент;
- нулевой элемент; , при этом
, при этом
 .
. и
и  противоположный элемент
противоположный элемент  .
. на
на  .
.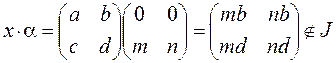 ,
, 
 по степеням
по степеням  и найти значения его производных в точке
и найти значения его производных в точке  .
.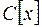 многочленов с комплексными коэффициентами следует, что
многочленов с комплексными коэффициентами следует, что
 . Коэффициенты многочлена
. Коэффициенты многочлена  удобнее находить по схеме Горнера (см. 2.4.), при этом все вычисления, как правило, оформляют в виде следующей таблицы – схемы:
удобнее находить по схеме Горнера (см. 2.4.), при этом все вычисления, как правило, оформляют в виде следующей таблицы – схемы:

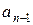





 на
на  так же по схеме Горнера
так же по схеме Горнера . Следовательно,
. Следовательно, .
.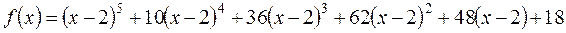 .
. , как непрерывно-дифференцируемую функцию, в окрестности точки
, как непрерывно-дифференцируемую функцию, в окрестности точки  можно разложить в ряд Тейлора следующим образом:
можно разложить в ряд Тейлора следующим образом: .
. получим, что
получим, что
 над кольцами Z [ x ] целочисленных многочленов, R [ x ] действительных многочленов и C [ x ] многочленов с комплексными коэффициентами.
над кольцами Z [ x ] целочисленных многочленов, R [ x ] действительных многочленов и C [ x ] многочленов с комплексными коэффициентами. . Непосредственной подстановкой убеждаемся, что ни одно из этих чисел не является корнем многочлена
. Непосредственной подстановкой убеждаемся, что ни одно из этих чисел не является корнем многочлена  , где p - делитель свободного коэффициента, а q - делитель старшего коэффициента. Для многочлена
, где p - делитель свободного коэффициента, а q - делитель старшего коэффициента. Для многочлена  . И вновь путём проверки выясняется, что лишь одно из этих чисел, а именно
. И вновь путём проверки выясняется, что лишь одно из этих чисел, а именно  , является корнем многочлена. На основании теоремы Безу, если число с является корнем многочлена
, является корнем многочлена. На основании теоремы Безу, если число с является корнем многочлена  , т.е.
, т.е.  .
. .
. не имеет рациональных корней. Разложение
не имеет рациональных корней. Разложение  найдём методом неопределённых коэффициентов, представив его в виде произведения двух многочленов второй степени, а именно
найдём методом неопределённых коэффициентов, представив его в виде произведения двух многочленов второй степени, а именно
 .
.
 , следовательно
, следовательно .
. не имеют целых корней, тогда искомое разложение над Z [ x ] найдено. Далее найдём корни последних многочленов второй степени:
не имеют целых корней, тогда искомое разложение над Z [ x ] найдено. Далее найдём корни последних многочленов второй степени:
 над R [ x ] выглядит следующим образом:
над R [ x ] выглядит следующим образом: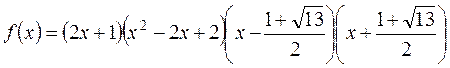 ,
, .
.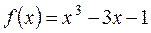
 , где
, где 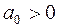 , следует, что его корни меньше числа
, следует, что его корни меньше числа  , где А - максимум модулей отрицательных его коэффициентов, а т - индекс первого отрицательного коэффициента в последовательности
, где А - максимум модулей отрицательных его коэффициентов, а т - индекс первого отрицательного коэффициента в последовательности  . Для данного многочлена
. Для данного многочлена  , следовательно, его корни не превышают числа
, следовательно, его корни не превышают числа  . Нижняя граница корней
. Нижняя граница корней  , взятого с противоположным знаком. В данном случае
, взятого с противоположным знаком. В данном случае ,
, больше числа
больше числа  . Итак корни, если они есть, находятся на промежутке
. Итак корни, если они есть, находятся на промежутке 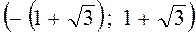 . Для того, чтобы определить, сколько их и в каких интервалах находятся, воспользуемся свойствами рядов Штурма. Алгоритм построения такого ряда гласит, что в качестве первого члена
. Для того, чтобы определить, сколько их и в каких интервалах находятся, воспользуемся свойствами рядов Штурма. Алгоритм построения такого ряда гласит, что в качестве первого члена  нужно взять сам многочлен, а в качестве
нужно взять сам многочлен, а в качестве  - его производную. Далее для всех
- его производную. Далее для всех 


