Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Из второго равенства получаем, чтоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Подставляя это выражение в первое равенство (3.1), получим:
Но из третьего равенства (3.1) следует, что
Подставляя это выражение в (3.3), получим:
В конце концов получаем:
Дробь вида (3.4) будем обозначать:
Представление (3.4) рационального числа называется конечной цепной или непрерывной дробью. Теорема. Всякое рациональное число может быть представлено в виде конечной цепной дроби. Дроби Выпишем реккурентные формулы для вычисления 1) 2) при 3) Числители и знаменатели двух соседних подходящих дробей связаны соотношением:
Примеры решения задач Задача №1 Выяснить, образует ли группу множество
всех линейных отображений числовой прямой на себя, относительно операции композиции отображения. Решение: Для того, чтобы множество
Проверим выполнимость вышеуказанных аксиом для множества
тогда
так как
Таким образом, нулевая аксиома выполняется. Далее, пусть
Отображения Рассмотрим элемент Проверим выполнимость четвёртой аксиомы. Для этого рассмотрим
Если Таким образом, если Если же Итак, не для всякого элемента множество Заметим, что если обозначить Задача №2 Доказать, что фактор-группа мультипликативной группы Решение: Для того, чтобы доказать требуемое, воспользуемся теоремой об изоморфизме, (см. п. 1.3).
Рассмотрим отображение Так как Задача №3 Найти порядок элемента Решение: Для того, чтобы найти порядок комплексного числа Ответ: 4 Задача №4 Пусть Решение: Для того, чтобы решить уравнение
то обратная перестановка
поэтому
Для того чтобы найти порядок перестановки Чётность перестановки можно определить по количеству инверсий в ней (см. п. 1.4.). Последнее определяется как количество таких пар элементов второй строки, в которых первым стоит число большее, нежели второе. Рассмотрим перестановку
Начнём с элемента 2, который стоит первым во второй строке. Он образует следующие пары: (24), (25), (26), (21) и (23), из которых лишь пара (21) образует инверсию. Далее элемент 4 и его пары: (45), (46), (41), (43). Инверсии образуют две пары (41) и (43). Элемент 5 образует инверсии с элементами 1 и 3. То же самое можно сказать и про элемент 6. Предпоследний элемент 1 образует лишь одну пару (13), но она инверсию не образует. Последний элемент 3 пар не образует (точнее его пары уже все рассматривались). Итак, количество инверсий перестановки Задача №5 Выяснить, является ли множество Решение: Для того чтобы множество
Кроме этого, если
Если же в коммутативном кольце Итак, нужно проверить выполняются ли все вышеуказанные аксиомы. Пусть
так как Аналогично
Для того чтобы убедиться, что верна и вторая часть рассматриваемой аксиомы, отдельно раскроем значения выражений Итак
Далее в качестве нулевого элемента рассмотрим
Аксиома (4) следует из свойств коммутативности для действительных чисел:
Теперь свойство дистрибутивности:
Аналогично проверяется справедливость 2-го свойства дистрибутивности Из всего вышесказанного следует, что множество A является коммутативным кольцом с единичным элементом
Далее для элемента
Тогда
Откуда
если Итак, Задача №6 Является ли идеалом множество Решение: Проверим, образует ли множество
2) так как 3) если
Из свойств 0) - 4) следует, что J является коммутативной группой по сложению. Заметим при этом, что аксиомы 1) – 4) можно было не проверять, так как они справедливы для всех элементов любого кольца в том числе и для тех его элементов, которые входят в J. Достаточно было бы проверить, что нулевой элемент кольца Теперь рассмотрим произведение Итак
Следовательно, J является лишь правым идеалом кольца Задача №7 Разложить многочлен
Решение: Согласно свойствам делимости в кольце
такой, что
В данном случае
или Далее разделим многочлен то есть
Тогда искомое разложение можно получить путём ещё 4-х кратного применения схемы Горнера. Все это можно оформить в виде таблицы – схемы.
Откуда
С другой стороны многочлен
Сравнивая коэффициенты при одинаковых степенях скобки,
Задача №8 Разложить на неприводимые множители многочлен Решение: Поиск разложения следует начать с поиска корней данного многочлена. На основании теоремы о рациональных корнях многочлена с целыми коэффициентами целочисленные корни следует искать среди делителей свободного коэффициента (см. 2.4.). В данном случае – среди делителей числа 6, то есть в множестве
Деление многочлена
Откуда
Где многочлен
Раскроем скобки и приравняем коэффициенты при одинаковых степенях x:
Получается система
Одним из решений которой является следующий набор переменных: A=-2; B=2; C=1; D=-3. Тогда
Так как многочлены
Откуда разложение
а над C [ x ]
Задача №9 С помощью ряда Штурма изолировать корни многочлена Решение: Сначала найдём границы корней данного многочлена (см. 2.4.). На основании теоремы о границе вещественных корней многочлена
тогда корни многочлена
Итак, в данном случае Далее разделим Таким образом, ряд Штурма для многочлена
Обозначим Все результаты вычислений занесём в таблицу, при этом, если при C= 0 получаем Итак,
Как утверждает теорема Штурма, на интервале Задача №10 Решить диофантово уравнение Решение: Для того, чтобы найти решение данного уравнения можно воспользоваться свойством линейной представимости наибольшего общего делителя чисел 43 и 51. Последнее можно найти с помощью алгоритма Евклида, последовательного деления с остатком. Для этого разделим 51 на 43 с остатком r1, далее делим 43 на r1 и получаем остаток r2, делим r1 на r2 и так далее, до тех пор пока не разделится без остатка. Последний, не равный нулю, остаток и есть Н.О.Д. (43,51). Для того, чтобы не запутаться делимое, делитель и остаток будет подчёркивать. Итак:
Из предпоследнего равенства выразим остаток 1=Н.О.Д. (43,51):
И, наконец, из первого равенства алгоритма Евклида
Итак, линейное представление наибольшего общего делителя чисел 43 и 51, получили:
где Итак,
где Ответ: Задача №11 Решить систему уравнений Решение: Рассмотрим поле
Учитывая, что число
Решим эту систему методом Гаусса. Ко второму уравнению прибавим первое, умноженное на
Из второго уравнения
В поле
Так как | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 (3.2)
(3.2) (3.3)
(3.3)
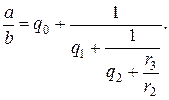
 (3.4)
(3.4)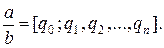
 и т.д. называются подходящими дробями цепной дроби (3.4).
и т.д. называются подходящими дробями цепной дроби (3.4). :
:




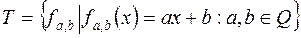
 являлось группой, необходимо и достаточно, чтобы на множестве его элементов было определено бинарная операция «
являлось группой, необходимо и достаточно, чтобы на множестве его элементов было определено бинарная операция « », обладающая следующими свойствами:
», обладающая следующими свойствами:
 ,
,
 ,если
,если 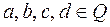 .
. тогда:
тогда:
 .
. и
и 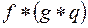 равны.
равны. . Тогда, если
. Тогда, если 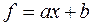 , то
, то  , аналогично
, аналогично  . Следовательно, в множестве
. Следовательно, в множестве  .
. , обозначим
, обозначим  , тогда
, тогда .
. , то
, то  . То есть
. То есть  . Так как
. Так как  , то
, то  если
если  .
. , то для
, то для 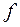 существует
существует  - обратный элемент.
- обратный элемент. , то есть
, то есть  , то для такого элемента
, то для такого элемента 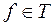 обратный элемент не существует.
обратный элемент не существует. множество элементов
множество элементов  с
с  , то
, то  образует группу относительно операции композиции отображений.
образует группу относительно операции композиции отображений. невырожденных рациональных матриц порядка
невырожденных рациональных матриц порядка  по подгруппе
по подгруппе  матриц с определителем, равным 1, изоморфна мультипликативной группе
матриц с определителем, равным 1, изоморфна мультипликативной группе  рациональных чисел, отличных от нуля.
рациональных чисел, отличных от нуля. , определённое следующим образом:
, определённое следующим образом: 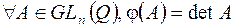 .
. , следовательно
, следовательно  гомоморфизм групп, при этом его образ
гомоморфизм групп, при этом его образ  , а ядро
, а ядро  . На основании теоремы следует, что
. На основании теоремы следует, что  , то есть
, то есть 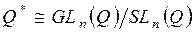 , что и требовалось доказать.
, что и требовалось доказать. мультипликативной группы
мультипликативной группы 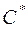 комплексных чисел без нуля.
комплексных чисел без нуля. (см. п. 1.1), нужно найти
(см. п. 1.1), нужно найти  . Итак,
. Итак, 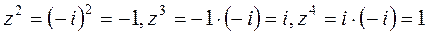 . Так как 1 является единичным элементом в группе
. Так как 1 является единичным элементом в группе  .
. . Решить уравнение
. Решить уравнение  . Найти порядок перестановки
. Найти порядок перестановки  . Определить чётность перестановки
. Определить чётность перестановки  .
. обратную к
обратную к  . Если перестановка
. Если перестановка  ,
, или
или 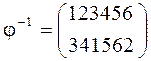 ,
, .
. . Следовательно,
. Следовательно,  .
. .
. . Число 7 является нечётным, следовательно, и перестановка
. Число 7 является нечётным, следовательно, и перестановка  кольцом (полем) относительно операций
кольцом (полем) относительно операций  и
и  .
. являлось кольцом относительно операций сложения
являлось кольцом относительно операций сложения 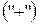 и умножения
и умножения 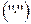 необходимо и достаточно выполнения следующих аксиом (см. 2.1.):
необходимо и достаточно выполнения следующих аксиом (см. 2.1.):
 , то кольцо называется коммутативным если
, то кольцо называется коммутативным если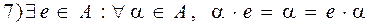 , то кольцо называется кольцом с единичным элементом.
, то кольцо называется кольцом с единичным элементом.
 , то
, то  тогда
тогда ,
,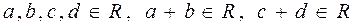 .
.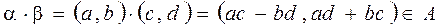 . Далее рассмотрим
. Далее рассмотрим
 и
и  .
.
 . Пусть
. Пусть  , то
, то  и наоборот
и наоборот  . Если
. Если  , то обратным к нему элементом является элемент, который можно обозначить
, то обратным к нему элементом является элемент, который можно обозначить  , так как
, так как

 .
.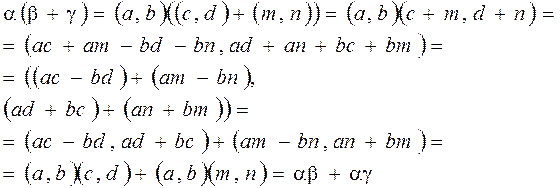
 .
. , так как
, так как
 найдём обратный элемент
найдём обратный элемент 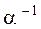 . Его «координаты» обозначим
. Его «координаты» обозначим  . Следовательно, должно выполняться равенство:
. Следовательно, должно выполняться равенство:  или
или  , то есть
, то есть .
. .
. ,
, .
. такой, что
такой, что  . Следовательно, A является полем.
. Следовательно, A является полем. в кольце
в кольце 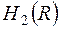 вещественных матриц
вещественных матриц  ?
? идеал в кольце
идеал в кольце  согласно определению (см. п. 2.3). Итак:
согласно определению (см. п. 2.3). Итак:
 - нулевой элемент;
- нулевой элемент; , при этом
, при этом
 .
. и
и  противоположный элемент
противоположный элемент  .
. на
на  .
.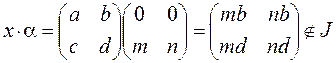 ,
, 
 по степеням
по степеням  и найти значения его производных в точке
и найти значения его производных в точке  .
. многочленов с комплексными коэффициентами следует, что
многочленов с комплексными коэффициентами следует, что
 . Коэффициенты многочлена
. Коэффициенты многочлена  удобнее находить по схеме Горнера (см. 2.4.), при этом все вычисления, как правило, оформляют в виде следующей таблицы – схемы:
удобнее находить по схеме Горнера (см. 2.4.), при этом все вычисления, как правило, оформляют в виде следующей таблицы – схемы:






 на
на  так же по схеме Горнера
так же по схеме Горнера . Следовательно,
. Следовательно, .
.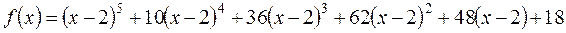 .
. , как непрерывно-дифференцируемую функцию, в окрестности точки
, как непрерывно-дифференцируемую функцию, в окрестности точки  можно разложить в ряд Тейлора следующим образом:
можно разложить в ряд Тейлора следующим образом: .
. получим, что
получим, что
 над кольцами Z [ x ] целочисленных многочленов, R [ x ] действительных многочленов и C [ x ] многочленов с комплексными коэффициентами.
над кольцами Z [ x ] целочисленных многочленов, R [ x ] действительных многочленов и C [ x ] многочленов с комплексными коэффициентами. . Непосредственной подстановкой убеждаемся, что ни одно из этих чисел не является корнем многочлена
. Непосредственной подстановкой убеждаемся, что ни одно из этих чисел не является корнем многочлена  , где p - делитель свободного коэффициента, а q - делитель старшего коэффициента. Для многочлена
, где p - делитель свободного коэффициента, а q - делитель старшего коэффициента. Для многочлена  . И вновь путём проверки выясняется, что лишь одно из этих чисел, а именно
. И вновь путём проверки выясняется, что лишь одно из этих чисел, а именно  , является корнем многочлена. На основании теоремы Безу, если число с является корнем многочлена
, является корнем многочлена. На основании теоремы Безу, если число с является корнем многочлена  , т.е.
, т.е.  .
. .
. не имеет рациональных корней. Разложение
не имеет рациональных корней. Разложение  найдём методом неопределённых коэффициентов, представив его в виде произведения двух многочленов второй степени, а именно
найдём методом неопределённых коэффициентов, представив его в виде произведения двух многочленов второй степени, а именно
 .
.
 , следовательно
, следовательно .
. не имеют целых корней, тогда искомое разложение над Z [ x ] найдено. Далее найдём корни последних многочленов второй степени:
не имеют целых корней, тогда искомое разложение над Z [ x ] найдено. Далее найдём корни последних многочленов второй степени:
 над R [ x ] выглядит следующим образом:
над R [ x ] выглядит следующим образом: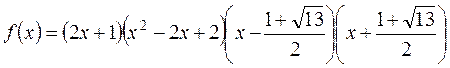 ,
, .
.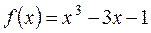
 , где
, где 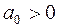 , следует, что его корни меньше числа
, следует, что его корни меньше числа  , где А - максимум модулей отрицательных его коэффициентов, а т - индекс первого отрицательного коэффициента в последовательности
, где А - максимум модулей отрицательных его коэффициентов, а т - индекс первого отрицательного коэффициента в последовательности  . Для данного многочлена
. Для данного многочлена  , следовательно, его корни не превышают числа
, следовательно, его корни не превышают числа  . Нижняя граница корней
. Нижняя граница корней  , взятого с противоположным знаком. В данном случае
, взятого с противоположным знаком. В данном случае ,
, больше числа
больше числа  . Итак корни, если они есть, находятся на промежутке
. Итак корни, если они есть, находятся на промежутке 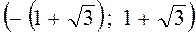 . Для того, чтобы определить, сколько их и в каких интервалах находятся, воспользуемся свойствами рядов Штурма. Алгоритм построения такого ряда гласит, что в качестве первого члена
. Для того, чтобы определить, сколько их и в каких интервалах находятся, воспользуемся свойствами рядов Штурма. Алгоритм построения такого ряда гласит, что в качестве первого члена  нужно взять сам многочлен, а в качестве
нужно взять сам многочлен, а в качестве  - его производную. Далее для всех
- его производную. Далее для всех  в качестве
в качестве 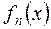 берётся остаток, с противоположным знаком с точностью до положительной константы, от деления
берётся остаток, с противоположным знаком с точностью до положительной константы, от деления  на
на  до тех пор, пока не получим многочлен нулевой степени.
до тех пор, пока не получим многочлен нулевой степени.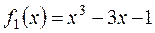 , т.к.
, т.к.  , то в качестве
, то в качестве  , т.е.
, т.е. 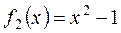 .
.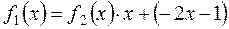 . Следовательно
. Следовательно  . Аналогично
. Аналогично  , откуда
, откуда  или в качестве последнего многочлена в ряде Штурма можно взять
или в качестве последнего многочлена в ряде Штурма можно взять  .
.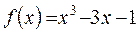 выглядит следующим образом:
выглядит следующим образом: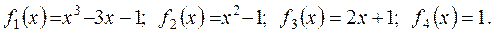
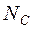 - количество перемен знаков в последовательности чисел
- количество перемен знаков в последовательности чисел  для всех
для всех  . Но для простоты вычислений в качестве C рассмотрим лишь целые числа, входящие в этот интервал, т.е.
. Но для простоты вычислений в качестве C рассмотрим лишь целые числа, входящие в этот интервал, т.е.  .
. , то в таблицу заносим лишь знаки этих чисел.
, то в таблицу заносим лишь знаки этих чисел.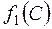





 многочлен
многочлен  . Поэтому на
. Поэтому на  количество корней равно
количество корней равно  . Следовательно, многочлен
. Следовательно, многочлен  имеет три действительных корня. Из построенной таблицы видно, что корни находятся в промежутках
имеет три действительных корня. Из построенной таблицы видно, что корни находятся в промежутках  , так как именно у них разница количества перемен знаков на концах равна одному, а у других – нулю.
, так как именно у них разница количества перемен знаков на концах равна одному, а у других – нулю. .
. .
. . Далее поднимемся строчкой выше. Выразим остаток
. Далее поднимемся строчкой выше. Выразим остаток  и подставим его в линейное представление Н.О.Д. (43,51) приведём подобные при подчёркнутых членах, т.е.
и подставим его в линейное представление Н.О.Д. (43,51) приведём подобные при подчёркнутых членах, т.е.  . Рассмотрим следующий остаток
. Рассмотрим следующий остаток 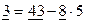 и тоже подставим и его:
и тоже подставим и его:
 . Следовательно
. Следовательно .
. . Умножим обе части этого равенства на 62, получим
. Умножим обе части этого равенства на 62, получим  . Следовательно, пара значений переменных
. Следовательно, пара значений переменных  является частным решением данного уравнения, а остальные решения могут быть найдены по формулам
является частным решением данного уравнения, а остальные решения могут быть найдены по формулам
 .
. При
При  Поэтому общий вид решений данного диофантного уравнения можно записать в виде
Поэтому общий вид решений данного диофантного уравнения можно записать в виде
 .
. над полями Z3 и Z5.
над полями Z3 и Z5. (см. 2.3.). Выпишем таблицы сложения и умножения для него
(см. 2.3.). Выпишем таблицы сложения и умножения для него



 , то систему нужно переписать в виде
, то систему нужно переписать в виде
 , а третье уравнение сложим тоже с первым. Получится
, а третье уравнение сложим тоже с первым. Получится
 , тогда из третьего
, тогда из третьего  . Откуда путём прибавления
. Откуда путём прибавления  к обеим частям получаем
к обеим частям получаем  , а после умножения на
, а после умножения на  . Теперь подставим найденные значения переменных в первое уравнение системы:
. Теперь подставим найденные значения переменных в первое уравнение системы:  , откуда
, откуда  . Итак, данная система над полем Z3 имеет единственное решение
. Итак, данная система над полем Z3 имеет единственное решение  таблицы сложения и умножения выглядят следующим образом:
таблицы сложения и умножения выглядят следующим образом: