
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон больших чисел. Неравенство Чебышева.Содержание книги
Поиск на нашем сайте
В широком понимании закон больших чисел – это принцип, согласно которому при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа СВ почти утрачивает случайный характер и становится законным. Узкое понимание закона больших чисел – ряд теорем, каждая из которых для тех или иных условий устанавливается фактическое приближение некоторых сравнительных характеристик большого числа СВ некоторым постоянным. Для любой СВ, имеющей матем.ожидание M(X)=a и дисперсию D(X), справедливо неравенство: P(|X-a|>ε)≤D(x)/ε^2 (1 форма). Учитывая, что события |X-a|>ε и |X-a|≤ε противопоожные, неравенство Чебышева можно записать и в другой форме: P(|X-a|≤ε)≥1-(D(x))/ε^2 (2 форма). Неравенство Чебышева для некоторых СВ во 2 форме примет вид: 1)для СВ X=m, имеющей биномиальный закон распр-я с мат.ожиданием M(X)=np и дисперсией D(X)=npq: P(|m-np|≤ε)≥1-npq/ε^2; 2)для частоты m/n события в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью M(m/n)=p и имеющей дисперсию D(m/n)=pq/n: P(|m/n-p|≤ε)≥1-pq/〖nε〗^2.
Закон больших чисел. Теорема Чебышева В широком понимании закон больших чисел – это принцип, согласно которому при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа СВ почти утрачивает случайный характер и становится законным. Узкое понимание закона больших чисел – ряд теорем, каждая из которых для тех или иных условий устанавливается фактическое приближение некоторых сравнительных характеристик большого числа СВ некоторым постоянным. Теорема Чебышева: Если дисперсия n-независимых СВ
Док-во: Обозначим
Запишем неравенство Чебышева в форме 2 P(|x-M(x)| M(x)=M D(x)=D С учетом того, что D(x)=
Заменив D(x) на
Переходя к пределу получаем
Ч.т.д. Отличие понятия сходимости и понятие сходимости по вероятности сост. в том, что если А – явл. пределом функции В случае сходимости по вероятности не существует жестких границ интервалов аналогичных неравенству (1). В частности для частоты событий Неравенство Чебышева: Если независимая СВ
Закон больших чисел. Теорема Бернулли В широком понимании закон больших чисел – это принцип, согласно которому при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа СВ почти утрачивает случайный характер и становится законным. Узкое понимание закона больших чисел – ряд теорем, каждая из которых для тех или иных условий устанавливается фактическое приближение некоторых сравнительных характеристик большого числа СВ некоторым постоянным. Теорема Бернулли: Частота события
Теорема Пуассона: Частота события
Закон больших чисел. Неравенство Маркова  , то для любого положительного А , то для любого положительного А  выполняется неравенство выполняется неравенство
Доказательство: Пусть
 - вероятности возможных значений СВ x. А – выберем таким, что оно будет принадлежать А - вероятности возможных значений СВ x. А – выберем таким, что оно будет принадлежать А 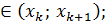
Переходя к противоположному событию получаем 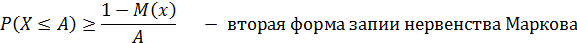
|
||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 198; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.237.52 (0.005 с.) |

 ограничены одной и той же постоянной, то при n стремящемся к ∞, средняя арифметическая СВ сходится по вероятности к средней арифметической их мат.ожидания.
ограничены одной и той же постоянной, то при n стремящемся к ∞, средняя арифметическая СВ сходится по вероятности к средней арифметической их мат.ожидания.

 – СВ; i=1,n D(
– СВ; i=1,n D( ); с=const; i=1,n
); с=const; i=1,n - мат.ожидание исходных СВ; i=1,n; Для СВ Х=
- мат.ожидание исходных СВ; i=1,n; Для СВ Х=
 )
) 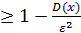
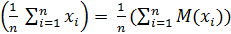 =
= 
 т.к.
т.к.  , получаем
, получаем D(x)
D(x) 

 получаем более точное неравенство
получаем более точное неравенство

 f(x) при х
f(x) при х  , то для всех х из
, то для всех х из  дельта окрестности точки
дельта окрестности точки  выполнялось условие
выполнялось условие  , т.е.
, т.е.  (1)
(1) , даже при достаточно больших n невозможно определить границы её изменения, хотя существует тенденция её сходимости к вероятности соответствующего события.
, даже при достаточно больших n невозможно определить границы её изменения, хотя существует тенденция её сходимости к вероятности соответствующего события. то при условии что их дисперсия ограниченна одной и той же постоянной имеет место
то при условии что их дисперсия ограниченна одной и той же постоянной имеет место
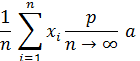
 сходится по вероятности к вероятности в отдельном испытании:
сходится по вероятности к вероятности в отдельном испытании: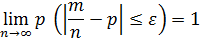
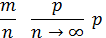



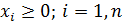

 В последнем равенстве отбросим 1-ые к слагаемые
В последнем равенстве отбросим 1-ые к слагаемые Заменив возможные значения СВ х на число А получим строгое неравенство:
Заменив возможные значения СВ х на число А получим строгое неравенство:
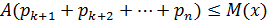
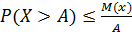 ч.т.д.
ч.т.д.


