
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая гипотеза. Общая схема ее проверки. Ошибки I и II ого рода.Содержание книги
Поиск на нашем сайте
Предположение относительно парам-ов распределения, а также сымих распределений, полученные в рез-те анализа стат. Данных наз-ся стат.гипотезами. Различают основную (нулевую) Н0 и конкурирующую (альтернативную) Н1 гипотезы. Основной наз-ся гипотеза, подлежащая проверке. Конкурирующая – гипотеза, по смыслу противоречащая основной. Основную гипотезу как правило выбирают в виде Н0: Конкурирующая: Н1: Выбор конкурирующей гипотезы влияет на вид критической области. Критической наз-ся область, возможные значения которой, соответствующие статистике критерия, отвергают основную гипотезу. Критическая область может быть односторонней (левосторонней или правосторонней) и двусторонней. Если Н1: Н1: Статистика критерия – СВ, определяемая по функции выборки, закон распределения которой хотя бы асимптотически ( Общая схема проверки стат.гипотез состоит в опр-ии: 1)основной и конкурирующей гипотез 2)статистики критерия 3)критической области 4)если статистика критерия оказалась в крит.области, то основная гипотеза отвергается. На выбранном уровне значимости, в противном случае основную гипотезу оставляют на последующие исследования. В рез-те проверки стат.гипотез возможны след.исходы: 1. Основная гипотеза верна и не отвергается в рез-те проверки 2. Основная гипотеза верна, но отвергается по выбранному числовому критерию (ошибка 1ого рода) 3. Основная гипотеза ошибочна, но принимается за верную по выбранному числовому критерию (ошибка 2ого рода) 4. Основаня гипотеза ошибочна и отвергается по выбранному критерию Пусть
tкр. – граница крит.области. опр-ся исходя из вида конкурирующей гипотезы, закона распределения статистики критерия, объема стат. Данных и заданного уровня значимости.
Сокращая ошибку 1ого рода происходит увеличение ошибки 2ого рода и наоборот уменьшая ошибку 2ого рода, увеличиваем 1ого рода. Границу кр.области целесообразно выбрать из решения реалиционной задачи где Значения Мощностью критерия называют вероятность недопущения ошибки 2ого рода. 1- Проверка гипотезы о равенстве средних двух совокупностей при неизвестных дисперсиях. Даны выборки Рассматривается основная гипотеза Н0: М(Х)=М(У) при конкурирующей гипотезе Н1: а)М(Х) Рассматривается числовой критерий
СВ Т распределена по закону Стьюдента со степенями свободы (n+m-2). Граница крит.области tкр. Выбирается по таблице крит.значений распределения Стьюдента. В пункте а) Н2 Н2
б) в) если в пункте а) наблюдаемое значение СВ |Т|< Проверка гипотезы о равенстве средних двух совокупностей при известных дисперсиях. Пусть m и n-объемы независимых выборок, по которым найдены соответствующие выборочные средние Х ̅ и У ̅. Проверим гипотезу Н0: М(Х)=М(У) при конкурирующей гипотезе Н1: а)М(Х) М(У), б) М(Х)>М(У)-левост.кр.обл. в)М(Х)<М(У)-правост.кр.обл. Во всех случаях вычисляется статистика критерия: Zнабл=(Х ̅-У ̅)/√((σ_x^2)/m+(σ_y^2)/n). В а) критическая точка zкр выбирается из условия Ф(zкр)=(1-α)/2. Если |Zнабл|<zкр, то гипотеза Н0 не отвергается, если |Zнабл|>zкр - отвергается. В б) критическая точка zкр выбирается из условия Ф(zкр)=0,5-α. Если Zнабл<zкр, то гипотеза Н0 не отвергается, если Zнабл>zкр - отвергается.
Гистограмма распределения. Первое, что можно получить из всякой конкретной выборки Х=(х1,х2,…,хn) – это начальное представление о законе распр-я. Осуществляется это путем построения так называемой гистограммы распр-я. Для этого опр-ся диапазон изменения возможных значений исследуемого признака (аналог СВ в ТВ) по имеющейся выборке Х=(х1,х2,…,хn) – от x’=min{xi} до x”= max{xi}. Этот диапазон условно подразделяется на М интервалов – так называемых разрядов, или «карманов» гистограммы. Число М выбирается исследователем. Согласно формуле Стерджеса рекомендуемое число М интервалов разбиения M Затем для i-го разряда (i=1,2,…,M) подсчитывается число mi попавших в него значений СВ. Полученные значения mi или
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.6.9 (0.006 с.) |

 , где
, где  - оценка пар-ра
- оценка пар-ра 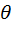 .
.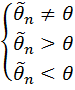
 , то крит.область двусторонняя.
, то крит.область двусторонняя. - односторонняя критическая область
- односторонняя критическая область ) сходится к одному из точных законов распределения.
) сходится к одному из точных законов распределения. - закон распределения признака х
- закон распределения признака х - закон распределения признака у
- закон распределения признака у Ошибка 1ого рода
Ошибка 1ого рода

 Ошибка 2ого рода
Ошибка 2ого рода
 и
и  - плата за единицу ошибки 1ого и 2ого рода соответственно.
- плата за единицу ошибки 1ого и 2ого рода соответственно. на практике не всегда можно определить, поэтому целесообразно наращивать объем анализируемых стат.данных.
на практике не всегда можно определить, поэтому целесообразно наращивать объем анализируемых стат.данных. и
и  предположительно отобранные из нормально распределенных генеральных совокупностей. Значения дисперсий признаков Х и У неизвестны, но предполагается, что Д(Х)=Д(У).
предположительно отобранные из нормально распределенных генеральных совокупностей. Значения дисперсий признаков Х и У неизвестны, но предполагается, что Д(Х)=Д(У).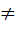 М(У), б) М(Х)>М(У)-левост.кр.обл. в)М(Х)<М(У)-правост.кр.обл.
М(У), б) М(Х)>М(У)-левост.кр.обл. в)М(Х)<М(У)-правост.кр.обл.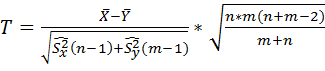

 - опр-ся по выборочным данным.
- опр-ся по выборочным данным.


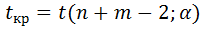
 . Если выбрать все разряды одинаковыми по ширине, то ширина разряда будет равняться: h=
. Если выбрать все разряды одинаковыми по ширине, то ширина разряда будет равняться: h=  .
. откладываются в масштабе по вертикали применительно к каждому разряду. Полученная таким образом гистограмма получила название гистограммы распределения признака Х:
откладываются в масштабе по вертикали применительно к каждому разряду. Полученная таким образом гистограмма получила название гистограммы распределения признака Х: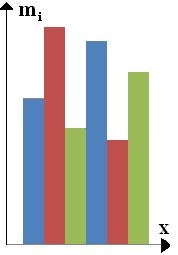 На основе гистограммы получаем первичное представление о виде закона распр-я исследуемого признака. При этом выполняются условия:
На основе гистограммы получаем первичное представление о виде закона распр-я исследуемого признака. При этом выполняются условия:  ;
;  .
.


