
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое ожидание СВ. Основные свойства.Содержание книги
Поиск на нашем сайте
Мат. ожиданием СВ наз-ся сумма произведений ее возможных значений на соотв-ие вероятности: Мх=М(х)= Мат. ожидание характ-т средневзвешенную оценку возможных значений СВ, т.е. центр тяжести возм-х значений СВ. СВОЙСТВА: 1. Мат. ожидание постоянной величины равно постоянной величине: М(с)=с, с-const; 2. Постоянный множитель можно выносить за знак мат. ожидания: М(к*х)=к*М(х), к-const; 3. Мат. ожидание от алгебраической суммы конечного числа СВ равно алгебраической сумме их мат. ожиданий: М(х 4. Если возможное значение СВ Х изменить на постоянную С, то мат. ожидание результата меняется на ту же постоянную С: М(х 5. Мат ожидание произведения конечного числа независимых СВ равно произведению их мат. ожиданий: М(х*у)=М(х)*М(у); Х и У- независимые СВ; 6. М(х*у)=М(х)*М(у)+Кху.
Дисперсия СВ. Основные свойства. Дисперсией СВ наз-ся мат. ожидание квадрата отклонения СВ от ее мат. ожидания: Dх=М((х-Мх)2). Дисперсия характ-т степень рассеивания возможных значений СВ относительно мат. ожидания. СВОЙСТВА: 1. D(с)=0, с-const; 2. Постоянный множитель можно выносить за знак дисперсии, возводя в квадрат: D(к*х)=к2D(х), к-const; 3. Дисперсия алгебраической суммы конечного числа независимых СВ равно сумме их дисперсий: D(х 4. Если возможные значения СВ меняются на постоянную С, то дисперсия при этом сохраняется: D(х 5. D(х)=М(х2)-М2(х); 6. D(х+у)=D(x)+D(y)+2Кxy. Средним квадратическим отклонением обозначается Типовые законы распределения дискретных СВ. Биномиальный закон распределение. Дискретная СВ Х с возможными значениями 0,1,2,3,…,n распределена по биномиальному закону, если вероятности ее возможных значений определяются по формуле: Р(x=m)= СВ Х с биномиальным законом распределения - это число экспериментов в серии из n независимых испытаний, в которых событие А наступило.
qn+npqn-1+…+pn=(q+p)n=1n=1 Параметрами распределения явл-ся n и p: разное количество экспериментов и разные вероятности. Многоугольник распределения можно построить для различных значений параметров этого распределения.
Частота события определяется по формуле P (x=
Типовые законы распределения дискретных СВ. Распределение Пуассона. Дискретная СВ Х распределена по закону Пуассона, если она принимает значения 0,1,2,…,m,... с вероятностями P(x=m)=
e-λ+ λ *e-λ +…+ Многоугольник распределения имеет вид (пример):
В сфере массового обслуживания с простейшим потоком событий число поступающих заявок - величина случайная с распределением Пуассона. Поток событий наз-ся простейшим, если он обладает свойствами: А) ординарности: вероятность поступления более 1 заявки на единичном интервале времени пренебрежительно мала; Б) стационарности: на равных интервалах времени поступает примерно равное число заявок; В) отсутствие последействия: число заявок на более позднем интервале времени никак не зависит от числа заявок на более раннем интервале времени.
Типовые законы распределения непрерывных СВ. Равномерный закон распределения. Непрерывная СВ Х распределена по равномерному закону, если плотность распределения ее вероятностей задается функцией f(х)= 0, х
Функция распределения СВ (F(x)=
1, х Числовые характеристики: М(х)= Числа, выработанные датчиком СВ – это СВ с равномерным законом распределения с параметрами а=0, в=1 по умолчанию. При условии, что х В играх (рулетка) угол остановки юлы имеет равномерный закон распределения с параметрами а=0, в=2
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.42.140 (0.006 с.) |

 ; x i -возможные значения СВ х, p i -вероятность того, что x=x i, i =
; x i -возможные значения СВ х, p i -вероятность того, что x=x i, i =  .
. у)=М(х)
у)=М(х)  х и наз-ся арифметическое значение квадратного корня из дисперсии:
х и наз-ся арифметическое значение квадратного корня из дисперсии:  х=
х= 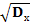 .
. pm(1-p)n-m.
pm(1-p)n-m. Числовые характеристики биномиально распределенной СВ определяются по формулам: M(x)=np, D(x)=npq,
Числовые характеристики биномиально распределенной СВ определяются по формулам: M(x)=np, D(x)=npq, 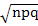 .
. , также величина случайная, распределенная по биномиальному закону. Возможные значения этой СВ 0;
, также величина случайная, распределенная по биномиальному закону. Возможные значения этой СВ 0;  ;
;  ;…;1.
;…;1. )=
)=  pm(1-p)n-m; M (
pm(1-p)n-m; M (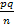 ;
;  .
.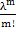 *e-λ, параметром распределения явл-ся λ=n*p.
*e-λ, параметром распределения явл-ся λ=n*p. /m!*e-λ
/m!*e-λ
 +
+  +…+
+…+  Мат. ожидание и дисперсия СВ, распределенной по закону Пуассона, равны и совпадают со значением параметра λ: M(x)=D(x)= λ.
Мат. ожидание и дисперсия СВ, распределенной по закону Пуассона, равны и совпадают со значением параметра λ: M(x)=D(x)= λ. (а;в);
(а;в); , х
, х  (а;в).
(а;в). ТЕОРЕМА
ТЕОРЕМА ), распределенной по равномерному закону, опр-ся функцией: F(x)= 0, х
), распределенной по равномерному закону, опр-ся функцией: F(x)= 0, х  а;
а; , а
, а  х
х  в.
в. ; D(х)=
; D(х)=  .
. .
.


