
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическое определение вероятности события.Содержание книги
Поиск на нашем сайте
Предмет теории вероятностей. Основные понятия. ТВ - раздел математики, занимающийся изучением закономерностей в массовых случайных явлениях. Случайным явлением называют явление, обладающее след. свойствами: неопределенности исхода, возможности воспроизведения, возможности измерения исхода каждого события. Для изучения случайных явлений используются 2 подхода: 1. Классический (детерменистский): закономерности случайных явлений определяются по основным факторам, чаще всего применяется в естественнонаучных исследованиях. Пренебрежение второстепенными факторами приводит к появлению элемента случайности в исследуемых явлениях. 2. Стохастический: используется в социально-экономических исследованиях, закономерности случайных явлений определяются как по основным, так и по второстепенным факторам. Полный учёт второстепенных факторов практически невозможен, поэтому результаты исследований носят вероятностный характер. К основным факторам относятся факторы, оказывающие сущ-ое влияние на исход испытания. К второстепенным относятся факторы с незнач. влиянием на исход испытания. Элемент случайности в явлениях снижается: при воспроизведении большего числа второстепенных факторов, с ростом массовых явлений. Событием называется всякий факт, который может (не)произойти при выполнении определенного комплекса условий (А, В,..., А1, А2). Различают достоверное (событие, которое наступает обязательно при выполнении комплекса условий), невозможное (событие, которое не может наступить при выполнении определенного комплекса условий) и случайное (все остальные события) событие. Вероятностью события называется численная мера объективной возможности наступления этого события (Р(А), р1,...). Свойства вероятности: вероятность достоверного события равна 1: Р(А)=1; вероятность невозможного события равна 0: Р(В)=0; вероятность случайного события определяется: 0<Р(С)<1. Два события А и В называются несовместными (или), если наступление одного из них исключает наступление другого. События называются совместными (и), если они могут появиться одновременно в одном испытании. События А1, А2,...,Аn называются единственно-возможными, если в результате испытания наступает хотя бы одно из этих событий. События А1, А2,...,Аn образуют полную группу событий, если являются возможно-несовместными и единственно-возможными. Два события, образующие полную группу называются противоположными. Под отрицанием события понимают наступление противоположного события: А, Вероятности событий, эксперименты по воспроизведению которых не обладают свойством симметрии исходов, определяются по частоте данного события или статистической вероятностью этого события. Статистической вероятностью события А называется отношение числа экспериментов, в которых событие наступило, к общему числу экспериментов: W(A)=P*(A)=m/n, где n-общее число экспериментов, m-число, в которых наступило событие А. Статистическая вероятность события - лишь оценка истинного значения вероятности этого события. Её использование возможно при выполнении след. условий: 1. Должны существовать возможности многократного воспроизведения экспериментов на предмет наступления события А при определенных условиях. 2 События должны обладать статистической устойчивостью или устойчивостью относительных частот. 3. Число экспериментов должно быть достаточно велико. Теорема Бернулли: С ростом числа экспериментов, т.е. при n→¥, относительная частота события сходится по вероятности к истинному значению вероятности этого события: Достоинством частотной схемы определения вероятности является широкий класс решаемых задач. Недостатками являются: приближенное значение вероятности события; большие моральные, материальные и временные затраты для получения этой оценки. Вероятность события - эксперимент, по воспроизведению которого можно разложить на равновозможные исходы равна: Р(А)=m/n, где n-общее число возможных исходов, m-число исходов, благоприятствующих событию А. Для нахождения значения m и n используют формулы комбинаторики. Сочетаниями из n по m называются соединения, состоящие из n элементов и отличающиеся друг от друга составом элементов. Число сочетаний из n по m равно числу способов выбора m элементов из имеющихся n: Если в сочетаниях выбираемые элементы могут повторяться, то их называют сочетаниями с повторениями: Размещениями из n по m называются соединения, состоящие из m элементов и отличающиеся друг от друга либо составом элементов, либо порядком их следования: Если в размещениях элементы могут повторяться, то их называют размещениями с повторениями: Перестановками из n элементов называются соединения, состоящие из n элементов, и отличающиеся друг от друга порядком следования элементов: Основные понятия мат.статистики Аналогом СВ из теории вероятности является признак Х в мат.статистике. Множество всевозможных значений признака Х, позволяющее оценить параметры распределения, а также само распределение признака Х с исчерпывающей точностью, называют генеральной совокупностью. Выборкой признака Х называют ограниченный объем стат.данных генеральной совокупности: Отбор выборочных данных из ген.совокупности – акт случайности ⇒ выборку можно рассмотреть как многомерную СВ. Значит, каждый элемент выборки – это СВ. Закон распределения выборки и её элементов совпадает с законом распределения ген.совокупности, их которых она извлечена. Основным св-ом выборки является её случайность. Это обеспечивает репрезентативность (представительность) выборки. В противном случае говорят об ошибке – презентативности.
Точечная оценка параметров распределения. Требования к функциям выборки. Функцией выборки называется нек-я ф-ция, переводящая элементы выборки в числовое значение. Функция выборки используется для оценки параметров распределения, границ доверительного интервала и оценки статистики критерия. Т.к.элементы выборки случайны, то число полученное по функции выборки- также величина случайная. Точечной оценкой Qn (с тильдой наверху) параметра распределения Q наз-ся величина, характеризующая истинное значение параметра Q. Для оценки одного и того же параметра распределения можно составить несколько различных функций выборки. Требования: 1.состоятельности -оценка параметра при n стремящимся к бесконечности сходится по вероятности к истинному значению этого параметра. Записывается так
Гистограмма распределения. Первое, что можно получить из всякой конкретной выборки Х=(х1,х2,…,хn) – это начальное представление о законе распр-я. Осуществляется это путем построения так называемой гистограммы распр-я. Для этого опр-ся диапазон изменения возможных значений исследуемого признака (аналог СВ в ТВ) по имеющейся выборке Х=(х1,х2,…,хn) – от x’=min{xi} до x”= max{xi}. Этот диапазон условно подразделяется на М интервалов – так называемых разрядов, или «карманов» гистограммы. Число М выбирается исследователем. Согласно формуле Стерджеса рекомендуемое число М интервалов разбиения M Затем для i-го разряда (i=1,2,…,M) подсчитывается число mi попавших в него значений СВ. Полученные значения mi или
Предмет теории вероятностей. Основные понятия. ТВ - раздел математики, занимающийся изучением закономерностей в массовых случайных явлениях. Случайным явлением называют явление, обладающее след. свойствами: неопределенности исхода, возможности воспроизведения, возможности измерения исхода каждого события. Для изучения случайных явлений используются 2 подхода: 1. Классический (детерменистский): закономерности случайных явлений определяются по основным факторам, чаще всего применяется в естественнонаучных исследованиях. Пренебрежение второстепенными факторами приводит к появлению элемента случайности в исследуемых явлениях. 2. Стохастический: используется в социально-экономических исследованиях, закономерности случайных явлений определяются как по основным, так и по второстепенным факторам. Полный учёт второстепенных факторов практически невозможен, поэтому результаты исследований носят вероятностный характер. К основным факторам относятся факторы, оказывающие сущ-ое влияние на исход испытания. К второстепенным относятся факторы с незнач. влиянием на исход испытания. Элемент случайности в явлениях снижается: при воспроизведении большего числа второстепенных факторов, с ростом массовых явлений. Событием называется всякий факт, который может (не)произойти при выполнении определенного комплекса условий (А, В,..., А1, А2). Различают достоверное (событие, которое наступает обязательно при выполнении комплекса условий), невозможное (событие, которое не может наступить при выполнении определенного комплекса условий) и случайное (все остальные события) событие. Вероятностью события называется численная мера объективной возможности наступления этого события (Р(А), р1,...). Свойства вероятности: вероятность достоверного события равна 1: Р(А)=1; вероятность невозможного события равна 0: Р(В)=0; вероятность случайного события определяется: 0<Р(С)<1. Два события А и В называются несовместными (или), если наступление одного из них исключает наступление другого. События называются совместными (и), если они могут появиться одновременно в одном испытании. События А1, А2,...,Аn называются единственно-возможными, если в результате испытания наступает хотя бы одно из этих событий. События А1, А2,...,Аn образуют полную группу событий, если являются возможно-несовместными и единственно-возможными. Два события, образующие полную группу называются противоположными. Под отрицанием события понимают наступление противоположного события: А, Вероятности событий, эксперименты по воспроизведению которых не обладают свойством симметрии исходов, определяются по частоте данного события или статистической вероятностью этого события. Статистической вероятностью события А называется отношение числа экспериментов, в которых событие наступило, к общему числу экспериментов: W(A)=P*(A)=m/n, где n-общее число экспериментов, m-число, в которых наступило событие А. Статистическая вероятность события - лишь оценка истинного значения вероятности этого события. Её использование возможно при выполнении след. условий: 1. Должны существовать возможности многократного воспроизведения экспериментов на предмет наступления события А при определенных условиях. 2 События должны обладать статистической устойчивостью или устойчивостью относительных частот. 3. Число экспериментов должно быть достаточно велико. Теорема Бернулли: С ростом числа экспериментов, т.е. при n→¥, относительная частота события сходится по вероятности к истинному значению вероятности этого события: Достоинством частотной схемы определения вероятности является широкий класс решаемых задач. Недостатками являются: приближенное значение вероятности события; большие моральные, материальные и временные затраты для получения этой оценки. Вероятность события - эксперимент, по воспроизведению которого можно разложить на равновозможные исходы равна: Р(А)=m/n, где n-общее число возможных исходов, m-число исходов, благоприятствующих событию А. Для нахождения значения m и n используют формулы комбинаторики. Сочетаниями из n по m называются соединения, состоящие из n элементов и отличающиеся друг от друга составом элементов. Число сочетаний из n по m равно числу способов выбора m элементов из имеющихся n: Если в сочетаниях выбираемые элементы могут повторяться, то их называют сочетаниями с повторениями: Размещениями из n по m называются соединения, состоящие из m элементов и отличающиеся друг от друга либо составом элементов, либо порядком их следования: Если в размещениях элементы могут повторяться, то их называют размещениями с повторениями: Перестановками из n элементов называются соединения, состоящие из n элементов, и отличающиеся друг от друга порядком следования элементов: Геометрическое определение вероятности события. В случаях, когда исходы испытания равняются равновозможными, а их число бесконечным множеством, вероятность некоторых событий можно определить как отношение меры благоприятствующей области к мере области, т.е. P(A)=m(G)/n(S). В качестве меры областей может выступать длина отрезка, площадь плоской фигуры или объем тела.
Рассмотрим плоскую фигуру S, внутри которой появляется случайная точка. Выделим подобласти S1 и S2. Событие A - случайно выбранная точка, окажется внутри заштрихованных областей S1 и S2. P(A)=(S1+S2)/S. Два события А и В называются несовместными (или), если наступление одного из них исключает наступление другого. События называются совместными (и), если они могут появиться одновременно в одном испытании. Если одно из событий произойдет обязательно, то такие события образуют полную группу событий. Суммой 2-х событий А и В называется событие С, состоящее в наступлении либо события А, либо события В: С=А+В. Произведением 2-х событий А и В называется событие С, состоящее в совместном наступлении как события А, так и В: С=A×B. Под отрицанием события А понимают наступление противоположного ему события: Теорема сложения совместных событий: Вероятность суммы 2-х совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления: P(A+B)=P(A)+P(B)–P(A×B). □ Пусть n-общее число возможных исходов, из них m способствуют наступлению события А, k благоприятствует событию В, l-число исходов, способствующих совместному наступлению А и В: Р(А)=m/n, Р(В)=k/n, P(A×B)=l/n, А+В→m+k-l. Р(А+В)=(m+k-l)/n=m/n+k/n–l/n= P(A+B)=P(A)+P(B)–P(A×B)■. Теорема сложения несовместных событий: Вероятность суммы 2-х несовместных событий равна сумме вероятностей этих событий: P(A+B)=P(A)+P(B). □ Т.к. А и B–несовместные события, то A×B–невозможное событие: P(A×B)=0. P(A+B)=P(A)+P(B)–0=P(A)+P(B)■. Следствие 1: Сумма вероятностей событий, образованных полную группу событий=1: Р(А1, А2,...,Аn)=1. □ Т.к. А1, А2,...,Аn образуют полную группу событий, то они попарно несовместно и является единственно возможными, тогда А1, А2,...,Аn–достоверное событие: Р(А1, А2,...,Аn)= Р(А1)+Р(А2)+...+Р(Аn)=1■. Следствие 2: Вероятность суммы противоположных событий=1: Р(А+ Два события А и В называются зависимыми, если вероятность наступления одного из них зависит от наступления другого события, в противном случае события независимые (если появление одного из событий не влияет на вероятность появления другого). Под условной вероятностью события А понимают вероятность этого события, вычисленную при условии, что событие В наступило: Р(А/В), РВ(А). Теорема (зависимость события) умножения: Вероятность произведения 2-х зависимых событий равна произведению вероятности одного из них на условную вероятность другого события: P(A×B)=Р(А)×Р(В/А)=Р(В)×Р(А/В). □ Пусть n-общее число возможных исходов, из них m благоприятствуют событию А, k-событию В, l-одновременно событию А и В: Р(В/А)=l/m=(l/n)/(m/n)= P(A×B)/Р(А)=> P(A×B)=Р(А)×Р(В/А). 1 из m исходов наступил 1/m (событие А наступило), из этих m исходов l способствуют наступлению события: Р(А/В)=l/k=(l/n)/(k/n)= P(A×B)/P(B)=> P(A×B)=Р(В)×Р(А/В)■. Для n зависимых событий теорема умножения вероятностей примет вид: Р(А1×А2×...×Аn)=Р(А1)×Р(А2/А1)×Р(А3/А1×А2)×...×Р(Аn/А1×А2×...×Аn-1). Р(А)=Р(А/В)=> А1×В -независимые события, Р(А)≠Р(А/В)=> А1×В -зависимые события.
7. Полная группа событий. Формула полной вероятности: Набор событий H1, H2, …, Hn называется полной группой попарно несовместных событий если:
Теорема: Если H1,H2,…,Hn – полная группа попарно несовместных событий, причем P(Hi)
8. Формула Байеса переоценки вероятностей гипотез. Ее практическое значение. Одним из самых важных следствий формулы полной вероятности является формула Байеса.
Используя формулу Байеса, мы оцениваем вероятность того, какая из возможных причин в действительности имела место при условии, что событие А произошло. Вероятности при
9. Формула Бернулли и Пуассона: Теорема Бернулли: если вероятность p наступления события А в каждом испытании постоянна, то вероятность Pm,n того, то событие А наступит m раз в n независимых испытаниях Бернулли, равна:
Формула Бернулли применяется при сравнительно небольших m и n. Теорема Пуассона: Если вероятность p наступления события А в каждом испытании стремиться к 0 (p->0) при неограниченном увеличении числа n испытаний (n->
Если вероятность p-постоянна и мала, число испытаний n-велико и число
10. Локальная и интегральная теоремы Муавра-Лапласа: Локальная: если вероятность p наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность
Функция f(x)-четная и для x Интегральная: если вероятность p наступления события А в каждом испытании постоянна и отлична от 0 и1, то вероятность того, что число m наступления события A в n независимых испытаниях заключено в пределах от a до b (включительно), при достаточно большом числе n приближенно равна:
Для положительных значений x существует таблицы значений функции Лапласа. Локальная и интегральная теоремы Муавра – Лапласа дают незначительную погрешность при Следствие: если вероятность p наступления события А в каждом испытании постоянна и отлична от 0 и1, то при достаточно большом числе n независимых испытаний вероятность того что: а) число m наступления события А отличается от произведения np не более, чем на величину e>0 (по абсолютной величине), т.е: б)частота
в)частота
11. Способа задания закона распределения дискретных случайных величин. Их свойства: Случайной называется величина, кот в результате испытания может принимать то или иное, значение заранее неизвестно какое именно. Различают: дискретные и непрерывные случайные величины. К дискретным относят случайные величины, возможные значения которых изолированы друг от друга и могут быть перечислены до опыта. Закон распределения ДСВ задается в виде ряда распределения.
X, p-соот. им вероятности. Предполагается, что независимые события X=x, i=1,2,…,n образуют полную группу. Следовательно имеет место следующее соотношение Свойства: 1)F(x) - неубывающая функция своего аргумента, т.е. при x1<x2 имеет место 2) 3)
12. Способы задания закона распределения непрерывных случайных величин. Их свойства: Случайной величиной называют непрерывной если ее возможное значение заполняют некоторый интервал в числовой оси. Законом распределения НСВ наз-ся всякое соотношение устанавливающее связь м/у возможными значениями случайно величины и соответствующим вероятностями. Ряд распределения – это таблица состоящая из2 строк, в первой из кот. указана возможные значения СВ, во второй соответ. им вероятности.
Функцией распределения СВ наз-ся вероятность того что СВ принимает значение меньше текущ.вел-ны X. Свойства: 1)F(x) - неубывающая функция своего аргумента, т.е. при x1<x2 имеет место 2) 3)
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.250 (0.011 с.) |

 .
. 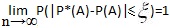 ,
,  .
. , где n>m.
, где n>m.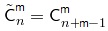 .
. .
.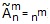 .
. .
.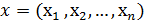 ;
;  - элементы выборки, n – объем выборки
- элементы выборки, n – объем выборки и так
и так  . 2.несмещенности - мат.ожидание оценок параметров распределения = истинному значению этого параметра.
. 2.несмещенности - мат.ожидание оценок параметров распределения = истинному значению этого параметра.  Если это равенство выполняется прия любых n, то это абсолютная несмещенность; а если при n стремящемся к бесконечности то асимптотическая. 3.эффективности - эффективной называют ту функцию выборки (оценку), к-я обладает наименьшей дисперсией.
Если это равенство выполняется прия любых n, то это абсолютная несмещенность; а если при n стремящемся к бесконечности то асимптотическая. 3.эффективности - эффективной называют ту функцию выборки (оценку), к-я обладает наименьшей дисперсией.  , где в числителе -дисперсия исследуемой оценки, в знаменателе -дисперсия эффективной оценки. Чем ближе коэффициет эффективности e к 1, тем эффективнее исследуемая оценка. Если это условие выполняется при n стремящемся к бесконечности, то это ассимптотическая эффективность.
, где в числителе -дисперсия исследуемой оценки, в знаменателе -дисперсия эффективной оценки. Чем ближе коэффициет эффективности e к 1, тем эффективнее исследуемая оценка. Если это условие выполняется при n стремящемся к бесконечности, то это ассимптотическая эффективность. . Если выбрать все разряды одинаковыми по ширине, то ширина разряда будет равняться: h=
. Если выбрать все разряды одинаковыми по ширине, то ширина разряда будет равняться: h=  .
. откладываются в масштабе по вертикали применительно к каждому разряду. Полученная таким образом гистограмма получила название гистограммы распределения признака Х:
откладываются в масштабе по вертикали применительно к каждому разряду. Полученная таким образом гистограмма получила название гистограммы распределения признака Х: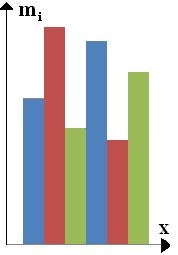 На основе гистограммы получаем первичное представление о виде закона распр-я исследуемого признака. При этом выполняются условия:
На основе гистограммы получаем первичное представление о виде закона распр-я исследуемого признака. При этом выполняются условия:  ;
;  .
. Вся область S и благоприятствующая область G должны быть замкнутыми и измеримыми.
Вся область S и благоприятствующая область G должны быть замкнутыми и измеримыми.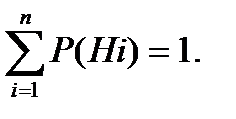 Пусть мы имеем полную группу несовместных событий H1, H2, …, Hn, определяющих варианты условий, в которых может осуществляться опыт по воспроизведению некоторого события А. Каждой гипотезе будет соответствовать своя условная вероятность события А: P(A/Hi), i=1,2,…,n.
Пусть мы имеем полную группу несовместных событий H1, H2, …, Hn, определяющих варианты условий, в которых может осуществляться опыт по воспроизведению некоторого события А. Каждой гипотезе будет соответствовать своя условная вероятность события А: P(A/Hi), i=1,2,…,n. 0, i=1,2,…,n,то для любого события А имеет место равенство:
0, i=1,2,…,n,то для любого события А имеет место равенство: - формула полной вероятности.
- формула полной вероятности. , i=1,2,…,n.
, i=1,2,…,n. -априорные вероятности.
-априорные вероятности.  -апостериорные вероятности. Процесс решения задач по формуле полной вероятности и формуле Байеса можно представить виде граф.схемы типа дерева, кот имеет одну корневую и несколько корневых вершин, соединенных м/у собой звеньями.
-апостериорные вероятности. Процесс решения задач по формуле полной вероятности и формуле Байеса можно представить виде граф.схемы типа дерева, кот имеет одну корневую и несколько корневых вершин, соединенных м/у собой звеньями.
 , где q=1-p.
, где q=1-p. )/. Причем произведение np стремится к постоянному числу
)/. Причем произведение np стремится к постоянному числу  (
( ), то вероятность того,что событие А появиться m раз n независимых испытаниях удовлетворяет предельному равенству.
), то вероятность того,что событие А появиться m раз n независимых испытаниях удовлетворяет предельному равенству.
 , получаем приближенную формулу Пуассона
, получаем приближенную формулу Пуассона
 , того что событие А произойдет m раз в n независимых испытаниях при достаточно большом числе n приближенно равна
, того что событие А произойдет m раз в n независимых испытаниях при достаточно большом числе n приближенно равна , где
, где  и
и  .
. [0;5] существует таблица значений. При x>5
[0;5] существует таблица значений. При x>5  .
. , где
, где - функция Лапласа;
- функция Лапласа; ,
,  .
.
 ;
; события А заключена в пределах от
события А заключена в пределах от  до
до  (включительно), т.е.
(включительно), т.е. , где
, где  ;
; 
 события А отличается от его вероятности p не более, чем на величину D>0(по абсолютной величине),т.е.
события А отличается от его вероятности p не более, чем на величину D>0(по абсолютной величине),т.е.

 ;
; ;
;



