
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перестановка. Циклы. Четность. СвойстваСодержание книги
Поиск на нашем сайте
Пусть В развернутой и наглядной форме перестановку
полностью указывая все образы:
Число различных перестановок из Множество всех перестановок длины Перестановки Например, для перестановок
имеем
В то же время
так что Умножение перестановок подчиняется следующим правилам. 1. Умножение ассоциативно, то есть 2. 3. Для каждой перестановки
Эти три свойства дают основание говорить о группе, называемой симметрической группой степени Разложим теперь перестановки
Перестановка Каждая перестановка Обратим внимание на циклы длины 2. Цикл длины 2 называется транспозицией. Любая транспозиция имеет вид Говорят, что элементы Если Если количество инверсий в перестановке
Утверждение. Пусть перестановка Свойства перестановок. 1. Произведение четных перестановок – четная перестановка. 2. Произведение четной перестановки на нечетную - есть нечетная перестановка. 3. Умножение на транспозицию меняет четность перестановки. 4. Четные перестановки образуют группу. 5. Перестановка и ей обратная имеют одинаковую четность. 6. Число четных и нечетных перестановок равно
2. Элементы теории колец (кольцо многочленов) Понятие кольца и поля. Свойства Кольцо – непустое множество 1) 2) 3) Если относительно умножения выполняется закон коммутативности, то кольцо коммутативно. Если в Элементы, у которых есть обратный элемент относительно умножения, называются единицами кольца (обратимыми элементами). Множество единиц кольца образует группу
Ненулевые элементы Если в кольце нет делителей нуля, отличных от самого нуля, то есть если из Коммутативное кольцо с единицей, в котором любой ненулевой элемент имеет обратный, называется полем. Область целостности – коммутативное кольцо с единицей, в которых нет делителей нуля.
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 2462; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.66.224 (0.008 с.) |

 - конечное множество из
- конечное множество из 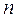 элементов. Поскольку природа его элементов для нас несущественна, удобно считать, что
элементов. Поскольку природа его элементов для нас несущественна, удобно считать, что 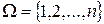 . Взаимно однозначное отображение
. Взаимно однозначное отображение 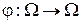 называется перестановкой из
называется перестановкой из 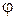 :
:  ,
,  , изображают двухрядным символом
, изображают двухрядным символом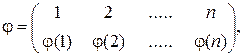
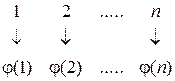 .
. чисел равно произведению
чисел равно произведению  , обозначаемому
, обозначаемому 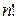 .
. .
. перемножаются в соответствии с общим правилом композиции отображений:
перемножаются в соответствии с общим правилом композиции отображений:  То есть под произведением перестановок будем понимать их суперпозицию.
То есть под произведением перестановок будем понимать их суперпозицию. ,
, 
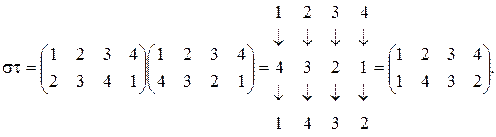

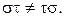
 для всех
для всех 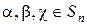 .
. :
: 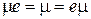 для всех
для всех 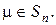
 существует обратная
существует обратная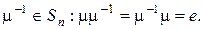

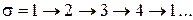 ,
, 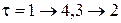
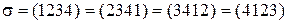 , носит название цикла длины 4, а перестановка
, носит название цикла длины 4, а перестановка  - произведение двух независимых (непересекающихся) циклов
- произведение двух независимых (непересекающихся) циклов 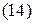 и
и 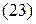 длины 2.
длины 2.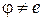 в
в  . Это разложение в произведение определено однозначно с точностью до порядка следования циклов.
. Это разложение в произведение определено однозначно с точностью до порядка следования циклов.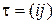 и оставляет на месте все символы, отличные от
и оставляет на месте все символы, отличные от 
 и
и 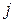 образуют относительно перестановки
образуют относительно перестановки 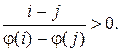
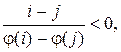 то элементы образуют неправильную пару, которая также называется инверсией.
то элементы образуют неправильную пару, которая также называется инверсией.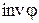 ) является числом четным (нечетным), то перестановка называется четной (нечетной).
) является числом четным (нечетным), то перестановка называется четной (нечетной). Знаком перестановки
Знаком перестановки 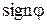 ) называется функция, определяемая следующим образом:
) называется функция, определяемая следующим образом: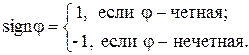
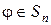 разложена в произведение независимых циклов длин
разложена в произведение независимых циклов длин 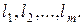 Тогда
Тогда 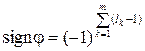 .
.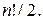
 с определенными на нем двумя бинарными операциями «+» и «
с определенными на нем двумя бинарными операциями «+» и «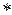 », условно называющимися сложением и умножением, удовлетворяющее следующим свойствам:
», условно называющимися сложением и умножением, удовлетворяющее следующим свойствам: – является коммутативной (абелевой) группой;
– является коммутативной (абелевой) группой; выполняется ассоциативный закон
выполняется ассоциативный закон 
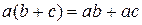 ,
,  .
.
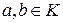 называются левым и правым соответственно делителями нуля, если
называются левым и правым соответственно делителями нуля, если 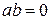 . Оказывается удобным и сам нуль считать делителем нуля.
. Оказывается удобным и сам нуль считать делителем нуля. следует, что или
следует, что или  , или
, или 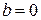 , то говорят о кольце без делителей нуля. Если, кроме того, кольцо коммутативно, то оно называется целостным.
, то говорят о кольце без делителей нуля. Если, кроме того, кольцо коммутативно, то оно называется целостным.


