
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центральные предельные теоремыСодержание книги Поиск на нашем сайте
Центральная предельная теорема (для одинаково распределенных слагаемых). Пусть X1, X2,…, Xn, …– независимые одинаково распределенные случайные величины с математическими ожиданиями M(Xi) = m и дисперсиями D(Xi) = где Ф(х) – функция стандартного нормального распределения. Эту теорему иногда называют теоремой Линдеберга-Леви [3, с.122]. В ряде прикладных задач не выполнено условие одинаковой распределенности. В таких случаях центральная предельная теорема обычно остается справедливой, однако на последовательность случайных величин приходится накладывать те или иные условия. Суть этих условий состоит в том, что ни одно слагаемое не должно быть доминирующим, вклад каждого слагаемого в среднее арифметическое должен быть пренебрежимо мал по сравнению с итоговой суммой. Наиболее часто используется теорема Ляпунова. Центральная предельная теорема (для разнораспределенных слагаемых) – теорема Ляпунова. Пусть X1, X2,…, Xn, …– независимые случайные величины с математическими ожиданиями M(Xi) = mi и дисперсиями D(Xi) = где Тогда для любого действительного числа х существует предел где Ф(х) – функция стандартного нормального распределения. В случае одинаково распределенных случайных слагаемых и теорема Ляпунова переходит в теорему Линдеберга-Леви. Теорема Линдеберга-Феллера. Пусть X1, X2,…, Xn, …– независимые случайные величины с математическими ожиданиями M(Xi) = mi и дисперсиями D(Xi) = где Fk (x) обозначает функцию распределения случайной величины Xk. Необходимое и достаточное условие многомерной сходимости [3, с.124]. Пусть Fn обозначает совместную функцию распределения k -мерного случайного вектора
Теорема о многомерной сходимости. Пусть Fn и Fλn – те же, что в предыдущей теореме. Пусть F - совместная функция распределения k -мерного случайного вектора Здесь сходимость Fn к F означает, что для любого k -мерного вектора
Предмет математической статистики. Математическая статистика — это раздел математики, посвященный методам сбора, анализа и обработки статистических данных для научных и практических целей. Статистические данные представляют собой данные, полученные в результате обследования большого числа объектов или явлений (то есть, математическая статистика имеет дело с массовыми явлениями). Методы анализа массовых явлений — предмет многих научных дисциплин; но только в том случае, когда для анализа привлекаются формальные (абстрактные) математические модели, эти методы становятся статистическими. Математическая статистика подразделяется на две обширные области:
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.240.219 (0.009 с.) |

 , i = 1, 2,…, n,… Тогда для любого действительного числа х существует предел
, i = 1, 2,…, n,… Тогда для любого действительного числа х существует предел
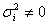 , i = 1, 2,…, n,… Пусть при некотором δ>0 у всех рассматриваемых случайных величин существуют центральные моменты порядка 2+δ и безгранично убывает «дробь Ляпунова»:
, i = 1, 2,…, n,… Пусть при некотором δ>0 у всех рассматриваемых случайных величин существуют центральные моменты порядка 2+δ и безгранично убывает «дробь Ляпунова»:

 (1)
(1)
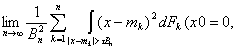
 , n = 1,2,…, и Fλn – функция распределения линейной комбинации
, n = 1,2,…, и Fλn – функция распределения линейной комбинации  . Необходимое и достаточное условие для сходимости Fn к некоторой k -мерной функции распределения F состоит в том, что Fλn имеет предел для любого вектора λ.
. Необходимое и достаточное условие для сходимости Fn к некоторой k -мерной функции распределения F состоит в том, что Fλn имеет предел для любого вектора λ. . Если функция распределения Fλn сходится при росте объема выборки к функции распределения Fλ для любого вектора λ, где Fλ – функция распределения линейной комбинации
. Если функция распределения Fλn сходится при росте объема выборки к функции распределения Fλ для любого вектора λ, где Fλ – функция распределения линейной комбинации  , то Fn сходится к F.
, то Fn сходится к F. такого, что функция распределения F непрерывна в
такого, что функция распределения F непрерывна в  где штрих обозначает операцию транспонирования вектора.
где штрих обозначает операцию транспонирования вектора.


