
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доверительный интервал. Доверительная вероятностьСодержание книги Поиск на нашем сайте
Пусть для параметра
Тогда диапазон практически возможных значений ошибки, возникающей при замене Перепишем (14.3.1) в виде:
Равенство (14.3.2) означает, что с вероятностью
При этом необходимо отметить одно обстоятельство. Ранее мы неоднократно рассматривали вероятность попадания случайной величины в заданный неслучайный интервал. Здесь дело обстоит иначе: величина
Рис. 14.3.1. Вероятность Дадим еще одно истолкование понятию доверительного интервала: его можно рассматривать как интервал значений параметра Перейдем к вопросу о нахождении доверительных границ Пусть для параметра
Метод наименьших квадратов является одним из наиболее распространенных и наиболее разработанных вследствие своей простоты и эффективности методов оценки параметров линейных эконометрических моделей. Вместе с тем, при его применении следует соблюдать определенную осторожность, поскольку построенные с его использованием модели могут не удовлетворять целому ряду требований к качеству их параметров и, вследствие этого, недостаточно “хорошо” отображать закономерности развития процесса Рассмотрим процедуру оценки параметров линейной эконометрической модели с помощью метода наименьших квадратов более подробно. Такая модель в общем виде может быть представлена уравнением (1.2): yt = a0 + a1 х1t +...+ an хnt + εt. Исходными данными при оценке параметров a0 , a1 ,..., an является вектор значений зависимой переменной y = (y1, y2,..., yT)' и матрица значений независимых переменных
в которой первый столбец, состоящий из единиц, соответствует коэффициенту модели Название свое метод наименьших квадратов получил, исходя из основного принципа, которому должны удовлетворять полученные на его основе оценки параметров: сумма квадратов ошибки модели должна быть минимальной. Статистической гипотезой Определения Пусть в (статистическом) эксперименте доступна наблюдению случайная величина
На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу. В большинстве случаев статистические критерии основаны на случайной выборке
\
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.111.109 (0.007 с.) |

 получена из опыта несмещенная оценка
получена из опыта несмещенная оценка  . Мы хотим оценить возможную при этом ошибку. Назначим некоторую достаточно большую вероятность
. Мы хотим оценить возможную при этом ошибку. Назначим некоторую достаточно большую вероятность  (например,
(например, 
 или
или  ) такую, что событие с вероятностью
) такую, что событие с вероятностью  , для которого
, для которого . (14.3.1)
. (14.3.1) ; большие по абсолютной величине ошибки будут появляться только с малой вероятностью
; большие по абсолютной величине ошибки будут появляться только с малой вероятностью  .
. . (14.3.2)
. (14.3.2) . (14.3.3)
. (14.3.3) . Случайно его положение на оси абсцисс, определяемое его центром
. Случайно его положение на оси абсцисс, определяемое его центром  , так как величина
, так как величина 
 и
и  называются доверительными границами.
называются доверительными границами. , нужно признать противоречащими опытным данным, а те, для которых
, нужно признать противоречащими опытным данным, а те, для которых  , - совместимыми с ними.
, - совместимыми с ними.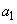 и
и 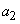 .
. .
Если X1,..., Xn — независимые случайные величины, одинаково нормально распределённые, причём EX i= a и DX i= s 2(i = 1,..., n), то при любых действительных значениях а и s > 0 отношение
.
Если X1,..., Xn — независимые случайные величины, одинаково нормально распределённые, причём EX i= a и DX i= s 2(i = 1,..., n), то при любых действительных значениях а и s > 0 отношение 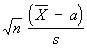 подчиняется С. р. с f = п- 1 степенями свободы (здесь
подчиняется С. р. с f = п- 1 степенями свободы (здесь 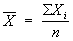 и
и  ). Это свойство было впервые (1908) использовано для решения важной задачи классической теории ошибок У. Госсетом (Англия), писавшим под псевдонимом Стьюдент (Student). Суть этой задачи заключается в проверке гипотезы а = a 0 (a 0 = заданное число, дисперсия s 2 предполагается неизвестной).
). Это свойство было впервые (1908) использовано для решения важной задачи классической теории ошибок У. Госсетом (Англия), писавшим под псевдонимом Стьюдент (Student). Суть этой задачи заключается в проверке гипотезы а = a 0 (a 0 = заданное число, дисперсия s 2 предполагается неизвестной).
 .
.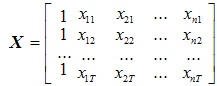
 .
. , распределение которой
, распределение которой  известно полностью или частично. Тогда любое утверждение, касающееся
известно полностью или частично. Тогда любое утверждение, касающееся  называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них: , где
, где  какой-то конкретный закон, называется простой.
какой-то конкретный закон, называется простой.  , где
, где  — семейство распределений, называется сложной.
— семейство распределений, называется сложной. 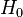 . Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза
. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза  , называемая конкурирующей или альтернативной.
, называемая конкурирующей или альтернативной. фиксированного объема
фиксированного объема  из распределения
из распределения 


