
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последовательность независимых испытаний. Формула Бернулли.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
На практике приходится сталкиваться с задачами, которые можно представить в виде многократно повторяющихся испытаний, в результате каждого из которых может появиться или не появиться событие А. При этом интерес представляет исход не каждого отдельного испытания, а общее число появлений события А в результате определенного количества испытаний. В подобных случаях нужно уметь определять вероятность любого числа m появлений события А в результате n испытаний. Рассмотрим случай, когда испытания являются независимыми и вероятность появления события А в каждом испытании одинакова и равна р,тогда Р( Монету подбрасывают 5 раз. Найти вероятность того, что герб появится 3 раза. Обозначим события: А - появление герба в одном испытании, В - герб появится 3 раза в серии из пяти испытаний. С помощью алгебраических действий событие В можно записать: В = ААА + В каждое произведение событие А входит 3 раза, а событие По формулам сложения и умножения получим Р(В) = Р(ААА = Запишем эту формулу в общем виде. Пусть Р(n,m) – вероятность того, что в n независимых испытаниях событие А наступит m раз. Тогда Р(n,m) = Доказательство формулы Бернулли аналогично решению рассмотренной выше задачи. Пример 9. Изделия некоторого производства содержат 5% брака. Найти вероятность того, что среди шести, взятых наудачу изделий: 1) будут два бракованных; 2) не будет бракованных; 3) будет хотя бы одно бракованное. Здесь А – появление бракованного изделия, Р(А) = 0,05, Р( n=6. По формуле Бернулли 1) при m = 2, Р(6,2) = 2) при m = 0, Р(6,0) = (0,95) 3) в этом случае задачу можно решить двумя способами. Первый способ. Используя формулу сложения, получим Р(6,1) + Р(6,2) = Второй способ. Перейдем к противоположному событию – среди выбранных изделий нет бракованных. Вероятность этого события вычислена в п.2) и равна 0,73. Тогда искомая вероятность Р(
Лекция 6. Наивероятнейшее число появлений события. Наивероятнейшим числом появления события А в n независимых испытаниях называется такое число m Р(n, m Для нахождения m
Решая совместно эти неравенства относительно m np – q Пример 10. Оптовая база снабжает 10 магазинов, от каждого из которых может поступить заявка на очередной день с вероятностью 0,4 независимо от заявок других магазинов. Найти наивероятнейшее число заявок в день и вероятность получения этого числа заявок. В данной задаче n = 10, p = 0,4, q = 1-p = 1 – 0,4 = 0,6. Подставим эти данные в приведенное выше неравенство 10 3,4 и окончательно, m Найдем теперь вероятность получения четырех заявок по формуле Бернулли Р(10,4) =
Статистическая оценка вероятности. Длительные наблюдения над появлением или не появлением события А при большом числе независимых испытаний в ряде случаев показывают, что число появлений события А подчиняется устойчивым закономерностям. Обозначим
n - число испытаний,
Статистическая вероятность обладает теми же свойствами, что и классическая вероятность, но при этом не требуется равновозможности исходов. Наиболее общим является аксиоматическое определение вероятности, которое сформулировал советский математик Колмогоров А.Н. в 1933 г..Однако это рассмотрение этого определения выходит за рамки данного курса лекций.
Случайные величины.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 425; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.195.90 (0.01 с.) |

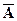 ) = 1 – р = q. Рассмотрим пример.
) = 1 – р = q. Рассмотрим пример. + А
+ А 
 .
.
 =
=  , это и есть формула Бернулли.
, это и есть формула Бернулли. .
. = 0,03;
= 0,03;
 0,73;
0,73;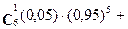
 1 – 0,73 = 0,27.
1 – 0,73 = 0,27. , для которого вероятность, соответствующая этому числу, не меньше вероятности каждого из остальных возможных чисел появления события А. Обозначим вероятность, соответствующую числу m
, для которого вероятность, соответствующая этому числу, не меньше вероятности каждого из остальных возможных чисел появления события А. Обозначим вероятность, соответствующую числу m  Р(n, m).
Р(n, m).

 m
m 
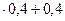 ,
, = 0,25.
= 0,25. - число появлений события А,
- число появлений события А, - частота появления события А при достаточно большом n сохраняет постоянную величину. Таким образом, под статистической вероятностью понимается относительная частота появления события А в n произведенных опытах.
- частота появления события А при достаточно большом n сохраняет постоянную величину. Таким образом, под статистической вероятностью понимается относительная частота появления события А в n произведенных опытах.


