
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Повторные независимые испытанияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Определение повторных независимых испытаний. Формула Бернулли и ее следствия. Наивероятнейшая частота появления события и ее вычисление. Локальная теорема Муавра-Лапласа. Функция
Л и т е р а т у р а
[2], гл.1, § 3, гл.5, § 3-5; [3], гл.4; [5], гл.5, § 1-4, гл.6, § 5,6; [6], гл.1; [7], гл.5, 6; [8], гл.2, § 1-3; [9], гл.2, § 1-5; [11], гл.28, § 189-195; [12], ч.2, гл.2, § 5-8; [13], гл.20, § 8; [15], гл.4, § 1-3.
О с н о в н ы е ф о р м у л ы и м е т о д и ч е с к и е у к а з а н и я Если производится n повторных независимых опытов, в каждом из которых появляется либо событие А с вероятностью р, либо событие Р n(m) = Вероятность того, что А появится хотя бы один раз при n повторных независимых испытаниях, вычисляется по следующей формуле: Рn (m ³ 1) = 1 – qn. (3.2) Наивероятнейшая частота m0 удовлетворяет неравенствам np – q £ m0 £ np + p. (3.3) Если число np+p – целое, то наивероятнейшее число m0 имеет только одно значение. Этим значением будет целая часть числа np+р. Если np+p – число дробное, то m0 принимает два значения: m0=np-q=np+p-1 и m0=np+p. При достаточно большом числе проведенных испытаний m0 примерно равно np (m0 » np). При большом числе испытаний для вычисления Рn(m) применяются следующие приближенные равенства: Рn(m)»
Рn(m)» В литературе обычно имеются таблицы значений функции Вероятность того, что событие А наступит не менее k раз и не более r раз, находится по приближенной формуле Р n (k £ m £ r)» Ф где Ф(х) = Формула (3.4) называется локальной теоремой Муавра-Лапласа, формула (3.6) – интегральной теоремой Муавра-Лапласа. Формулу (3.5) называют теоремой Пуассона. Вероятности отклонений частоты m от наивероятнейшей частоты m0 и относительной частоты W от постоянной вероятности р события А при достаточно больших n вычисляются, соответственно, по следующим приближенным формулам: Р n Р n где Ф(х) – функция Лапласа и При n®¥ величина 2Ф При практическом применении теории вероятностей часто встречаются задачи на повторение опытов (испытаний). Многие же задачи моделируются как задачи на повторные испытания. Решаются они просто в случае, когда опыты являются независимыми. В этом прежде всего и надо убедиться. В каждом отдельном опыте появляется либо событие А, либо ему противоположное Может быть и более общая схема: независимые опыты производятся в различных условиях (вероятность события А от опыта к опыту меняется). Имеется способ вычисления Р n(m) и в этой ситуации (см., например, [3]). Примерами независмых опытов являются: неоднократное бросание монеты (игральной кости), многократное извлечение карты из колоды (шара из урны, изделия из партии) при условии, что выбранный предмет возвращается. Иногда допускают ошибку. В отборах без возвращения применяют биномиальное распределение (формулу Бернулли), на самом же деле надо применять гипергеометрическое распределение. Поясним это разбором задачи. В урне находятся 5 белых и 10 черных шаров. Из урны наугад извлекли 3 шара. Какова вероятность того, что два из них окажутся белыми? Решение (ошибочное). Обозначим через А событие, состоящее в том, что отдельно взятый шар будет белым. Тогда, согласно условию, за р принимают число Р 3(2) =
Приведенное решение было бы верным, если бы опыты проводились в неизменных условиях. Для этого шары надо обратно возвращать в урну и перемешивать. По условию нашей задачи из урны вынули три шара (следовательно, они не возвращались). В этом случае уже нельзя говорить о неизменности условий всех трех опытов, так как после каждого извлечения состав шаров в урне будет меняться. Для правильного решения применим классический способ подсчета вероятностей. Число возможных исходов будет Формула Бернулли (3.1) дает точное значение Р n(m), однако для больших значений n и m появляются вычислительные трудности, прежде всего из-за выражения для Поэтому возникает необходимость в более простых формулах для Р n(m). Таковыми являются формулы (но уже приближенные) (3.4) и (3.5). Формула (3.4) дает тем более близкие к точному значению Р n(m) результаты, чем больше значение Найдем наибольшее значение выражения pqºр(1-р). Рассмотрим функцию f(р)=р(1-р)ºр-р2, 0 £ р £ 1. Очевидно, что она достигает своего наибольшего значения В случае, если вероятность р близка к нулю и число n мало, формула (3.4) дает заметные отклонения от формулы Бернулли. Асимптотическая формула (3.5) применяется для редких событий (со значениями р, близкими к нулю). Приближение тем лучше, чем больше n и меньше p. Обычно формулой (3.5) пользуются при условии Задачи с редкими событиями встречаются на практике в лотереях, страховании, при проверке качества изделий с низким процентом брака, в медицине (рождение близнецов, заболевание редкой инфекционной болезнью) и т.п. Если р близко к единице (например, р³0,97), то q близко к нулю (q£0,03). Тогда формулу Пуассона (3.5) можно применить для вычисления вероятности того, что Как уже отмечалось, для функций Поясним метод линейного интерполирования для нашей ситуации. Аргумент y-y1= В ряде учебников имеются таблицы значений функции р(m, Если число n независимых испытаний мало и надо вычислить вероятность появления события А от k до r раз, то надо применить следующую формулу: Р n(k £ m £ r) = Эту последнюю формулу можно применять и при достаточно большом числе испытаний, если в сумме справа число слагаемых невелико (мало число r-k). При этом для вычисления Р n(m) при малых значениях р (р£0,03) надо применять приближенную формулу (3.5), а в остальных случаях – (3.4). Если же число n велико и число слагаемых в сумме В этой формуле участвует функция Лапласа Ф(х), называемая еще интегралом вероятностей. Значения этой функции приводятся почти в каждом из рекомендуемых учебников. Только надо помнить, что в ряде учебников (см., например, [7], [8], [11]) эти значения удвоены. Тогда в (3.6) надо подставлять значения в два раза меньшие (можно также, не уменьшая этих значений, ввести справа в (3.6) множитель Таблицы Ф(х) приведены для х ³0. Для отрицательных аргументов значения этой функции находятся на основании ее свойства, что Ф(- х) = -Ф(х). Например, Ф(-2) = -Ф(2)» -0,4 772 (см. [5], приложение 2). Далее, для х >5 приближенно полагают Ф(х)» Сделаем некоторые пояснения по поводу формулы (3.8). Прежде всего она имеет теоретическое значение. Из нее следует так называемый закон больших чисел Бернулли, который будет рассмотрен в дальнейшем. Она объясняет, что статистическое определение вероятности события введено разумно. Эта формула имеет значительные практические приложения. Зная р, n и e, из (3.8) находим надежность g. Если известны р, n и g, то можно найти точность e. Наконец, что очень важно на практике, можно по р, заданным e и g оценить число n (число испытаний, необходимых для какого-нибудь контроля). Более того, можно оценить n только при известных e и g (р- неизвестно). Надежность g приближенно получается из равенства (3.8): g = 2Ф Обозначим через
Решая уравнение (3.9) (g = 2Ф( e = Тогда с надежностью g определяются границы, в которых заключены частость и частота события в серии из n испытаний:
Из (3.10) получается и формула для определения необходимого числа n испытаний при известных р, g, e:
Из последнего равенства при неизвестном р в силу оценки pq=p(1-p)£
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.128.81 (0.012 с.) |

 и ее свойства. Формула Пуассона и ее приложения. Интегральная теорема Муавра-Лапласа. Функция Лапласа и ее свойства. Вероятности отклонений частоты от наивероятнейшей частоты и относительной частоты от вероятности появления события.
и ее свойства. Формула Пуассона и ее приложения. Интегральная теорема Муавра-Лапласа. Функция Лапласа и ее свойства. Вероятности отклонений частоты от наивероятнейшей частоты и относительной частоты от вероятности появления события. с вероятностью q=1-р, то вероятность Р n(m) того, что событие А появится ровно m раз, выражается формулой Бернулли
с вероятностью q=1-р, то вероятность Р n(m) того, что событие А появится ровно m раз, выражается формулой Бернулли рm qn-m. (3.1)
рm qn-m. (3.1) (3.4)
(3.4)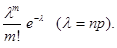 (3.5)
(3.5)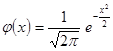 и выражения р(m, λ) =
и выражения р(m, λ) =  .
. - Ф
- Ф  , (3.6)
, (3.6)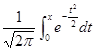 - функция Лапласа, для которой имеется таблица значений.
- функция Лапласа, для которой имеется таблица значений. Ф
Ф  , (3.7)
, (3.7)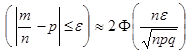 , (3.8)
, (3.8)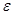 - любое положительное число.
- любое положительное число. Ф
Ф 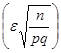 стремится к единице. Тогда событие
стремится к единице. Тогда событие  практически достоверно. Если число
практически достоверно. Если число 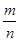 этого события. Величина
этого события. Величина 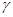 , определяемая равенством
, определяемая равенством 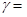 Р n
Р n 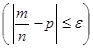 , называется надежностью. Таким образом, надежность есть вероятность совпадения частоты W=
, называется надежностью. Таким образом, надежность есть вероятность совпадения частоты W=  .
. : р=
: р= 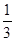 , q=
, q=  . Далее, полагают n=3, m=2. Вероятность искомого события (два белых шара при вынутых трех) вычисляют по формуле Бернулли:
. Далее, полагают n=3, m=2. Вероятность искомого события (два белых шара при вынутых трех) вычисляют по формуле Бернулли: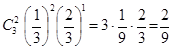 .
.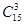 , из них благоприятными для интересующего нас события будут
, из них благоприятными для интересующего нас события будут  исходов. Тогда искомая вероятность Р =
исходов. Тогда искомая вероятность Р = 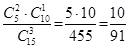 .
.
 . При этом здесь сказывается не только значение n, но и значение pq. Обычно формулой (3.4) пользуются, когда npq³20. Из этого ограничения видно, что чем ближе одно из чисел p или q к нулю (другое число будет близко к единице), тем большим надо брать n. Погрешность этой формулы порядка
. При этом здесь сказывается не только значение n, но и значение pq. Обычно формулой (3.4) пользуются, когда npq³20. Из этого ограничения видно, что чем ближе одно из чисел p или q к нулю (другое число будет близко к единице), тем большим надо брать n. Погрешность этой формулы порядка 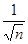 .
.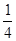 при р=
при р= 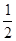 . Следовательно, при одних и тех же значениях n формула (3.4) дает тем лучшее приближение к значению Р n(m) из формулы Бернулли, чем ближе pq к своему наибольшему значению 0,25, т.е. чем ближе р (отсюда и q) к 0,5.
. Следовательно, при одних и тех же значениях n формула (3.4) дает тем лучшее приближение к значению Р n(m) из формулы Бернулли, чем ближе pq к своему наибольшему значению 0,25, т.е. чем ближе р (отсюда и q) к 0,5. =np£10. Погрешность формулы (3.5)
=np£10. Погрешность формулы (3.5) 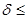 np2.
np2.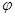 (х) и р(m,
(х) и р(m, 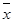 , которого нет в таблице, будет заключен между некоторыми двумя аргументами х 1 и х 2, имеющимися в таблице (х 1 <
, которого нет в таблице, будет заключен между некоторыми двумя аргументами х 1 и х 2, имеющимися в таблице (х 1 < 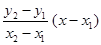 ; ограничение х 1 ¹ х 2 выполняется автоматически, т.к. х 1< х 2. Получилась линейная функция y=
; ограничение х 1 ¹ х 2 выполняется автоматически, т.к. х 1< х 2. Получилась линейная функция y= 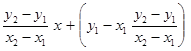 . Значение этой линейной функции в точке
. Значение этой линейной функции в точке  для некоторых m и
для некоторых m и 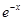 (одного множителя нашей функции). Значения второго множителя
(одного множителя нашей функции). Значения второго множителя 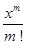 при небольших значениях m легко вычислить.
при небольших значениях m легко вычислить. Р n(m). В этой ситуации k и r не могут быть большими (мало n) и все Р n(m) можно вычислить по формуле Бернулли. Приведенная формула есть следствие теоремы о вероятности суммы попарно несовместных событий.
Р n(m). В этой ситуации k и r не могут быть большими (мало n) и все Р n(m) можно вычислить по формуле Бернулли. Приведенная формула есть следствие теоремы о вероятности суммы попарно несовместных событий. при х ®+¥.
при х ®+¥.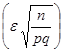 . (3.9)
. (3.9)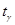 величину e
величину e 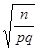 :
: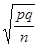 .
.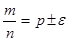 ,
, 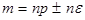 .
.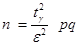 .
.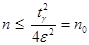 , т.е. достаточно провести n0 испытаний для определения неизвестной вероятности р появления события с заданной точностью и надежностью.
, т.е. достаточно провести n0 испытаний для определения неизвестной вероятности р появления события с заданной точностью и надежностью.


