
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
На практике для вычисления дисперсии применяется формулаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте ДВ = где При вычислении Выборочным средним квадратическим отклонением (стандартом) sВ называется квадратный корень из выборочной дисперсии: sВ = Начальный эмпирический момент порядка k
Отсюда мы видим, что начальный эмпирический момент первого порядка (k=1) равен выборочной средней Центральный эмпирический момент mk порядка k определяется равенством mk= Отсюда видно, что m2=ДВ, т.е. центральный эмпирический момент второго порядка совпадает с выборочной дисперсией. Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h. Варианты Ui, определяемые равенством Ui = называются условными. Здесь х i – первоначальные равноотстоящие варианты, h – разность прогрессии (шаг), С – ложный нуль (новое начало отсчета). В качестве ложного нуля можно принять любую варианту. Обычно в качестве ложного нуля выбирают варианту с наибольшей частотой или варианту, стоящую в середине вариационного ряда. Условные варианты являются целыми числами. При этом варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю. Условные эмпирические моменты
Легко установить, что
ДВ = [ Метод произведений есть некоторый удобный способ вычисления условных моментов различных порядков в случае равноотстоящих вариант. По условным моментам можно найти начальные и центральные эмпирические моменты. Вычислять условные моменты Размахом варьирования R называют разность между наибольшей и наименьшей вариантами: R = х max – x min. (9.14) Размах есть самая простая характеристика рассеяния вариационного ряда. Еще одной характеристикой рассеяния служит среднее абсолютное отклонение Q, которое определяется равенством Q = Коэффициент вариации V определяется по формуле V = Он служит для сравнения величин рассеяния двух вариационных рядов. Большее рассеяние имеет тот ряд, у которого коэффициент вариации больше. Важными числовыми характеристиками являются мода и медиана. Для дискретного статистического ряда мода есть значение признака, имеющего наибольшую частоту. Определим теперь моду интервального ряда в случае постоянной длины h всех интервалов. Пусть (х k, х k+1) – модальный интервал, т.е. интервал, которому соответствует наибольшая частота nk. Пусть nk-1 – частота интервала, предшествующего модальному, а nk+1 – частота интервала, следующего за модальным. Тогда мода М0 вычисляется по формуле М0 = х k + h × Медианой Ме называется такое значение признака, относительно которого статистический ряд делится на две части, причем в одной из них содержатся члены, у которых значения не больше Ме, а в другой – члены со значениями не меньше чем Ме. Пусть выборка дискретна и значения признака различны. Если число вариант четное (n=2k), то Ме = Если число вариант нечетное (n=2k+1), то Ме = х k+1. (9.19) Пусть выборка дискретна и значения признака повторяются. Если объем статистической совокупности является нечетным числом, то в качестве медианы берут такое значение признака Х, для которого накопленная частота SH (сумма частот вариант, не превосходящих данного значения) равна SH = Если объем выборки является четным числом, то Ме определяется равенством Ме = где Если статистический ряд задан интервалами, то медиану находят следующим образом. Выявляют первый интервал, для которого накопленная частота равна или больше половины объема статистической совокупности Ме = где х k- левая граница медианного интервала; Sk-1 – накопленная частота интервала, предшествующего медианному; nk – частота медианного интервала. Асимметрия a и эксцесс e эмпирического распределения определяются равенствами:
где m3, m4 – центральные эмпирические моменты, соответственно, третьего и четвертого порядка. Эти характеристики используют для оценки отклонения эмпирического распределения от нормального.
Р е ш е н и е т и п о в ы х з а д а ч
Задача 1. Выборка шарикоподшипников, изготовленных станком-автоматом, дала после измерения на весах следующие результаты в граммах: 39, 41, 40, 40, 43, 41, 44, 42, 41, 41, 43, 42, 39, 40, 42, 43, 41, 42, 41, 39, 42, 42, 41, 42, 40, 41, 43, 41, 39, 40. Составить статистическое распределение выборки. Построить полигоны частот и относительных частот. Решение. Значения х i вариант выборки (вес шарикоподшипников) расположим в порядке возрастания в первой строке таблицы, а во второй строке – количество шарикоподшипников этого веса (частоты):
Получили дискретное статистическое распределение выборки объема n=Sni = 4+5+9+7+4+1=30. Мода М0=41. Построим полигон частот. Для этого откладываем по оси О х значения х i вариант выборки, а по оси ординат – частоты ni. Полученные точки соединяем отрезками прямых. Это и будет полигон частот (см.рис. ниже).
0 39 40 41 42 43 44 х
Полигон относительных частот строится аналогично полигону частот. На оси ординат вместо частот ni откладываем относительные частоты Wi. Полигон относительных частот изображен ниже на рисунке.
Задача 2. Составить статистическое распределение выборки – рабочих по процентам выполнения норм выработки, если произведена случайная выборка объема 20 человек и получены такие данные относительно выполнения ими норм выработки в процентах: 127, 121, 112, 114, 131, 117, 109, 107, 155, 135, 103, 145, 99, 100, 97, 102, 122, 115, 132, 105. Построить гистограммы частот и относительных частот. Решение. Находим наибольшее и наименьшее значения варианты Х: х наиб=155, х наим=95. Разобьем здесь объем выборки на 7 промежутков длиной h=10. Частичные промежутки расположим в первой строке таблицы, а во второй – количество рабочих, чья выработка заключена в данном частичном промежутке. Получим следующее интервальное распределение:
Построим гистограмму частот распределения. Для этого по оси O х отложим промежутки распределения выборки и на них как на основаниях строим прямоугольники, высоты которых равны соответственно
Нетрудно убедиться, что площадь построенных прямоугольников равна объему выборки:
Гистограмму относительных частот строим аналогично гистограмме частот. Только на оси ординат вместо
Сумма площадей построенных прямоугольников равна единице. Задача 3. Данные о продаже женской обуви в магазине за день заданы таблицей
Найти эмпирическую функцию распределения выборки и построить ее график. Решение. Эмпирическую функцию распределения выборки находим по формуле (9.1). Объем выборки равен 4+5+9+7+4+1=30. Наименьшая варианта равна 35. Значит, F*(х)=0 при х £35. Значения Х <36, т.е. х 1=35 наблюдались 4 раза. Следовательно, F*(х)= F*(х) = График этой функции изображен на рисунке.
0 х Задача 4. Распределение урожайности сои на площади в 1000 га дано в таблице
Определить выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение урожайности сои. Решение. Выборочная средняя урожайности с га вычисляется по формуле (9.4):
Для определения выборочной дисперсии воспользуемся формулой (9.6). Получим ДВ = + Выборочное среднее квадратическое отклонение sВ находим по формуле (9.8): sВ = Задача 5. Вычислить выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение и коэффициент вариации для распределения заработной платы водителей автобазы (в руб. за месяц):
Решение. Превратим данный интервальный ряд в дискретный, взяв в качестве вариант середины интервалов:
По формуле (9.4) выборочной средней найдем, что
Вычислим выборочную дисперсию по формуле (9.7): ДВ = Извлекая корень квадратный из дисперсии, получим выборочное среднее квадратическое отклонение sВ = Коэффициент вариации заработной платы водителей автобазы вычислим по формуле (9.16): V = Задача 6. Дано следующее статистическое распределение выборки:
Вычислить начальные и центральные моменты первого, второго и третьего порядка, размах варьирования и среднее абсолютное отклонение. Решение. Используя формулу (9.9), находим начальные моменты:
Центральные моменты вычисляем по формуле (9.10): m1=0, m2=ДВ= Используя формулы (9.14) и (9.15), получим R=8-3=5, Q= Задача 7. Магазин в течение месяца реализовал 100 мужских костюмов. Распределение их по размерам дано таблицей
Найти модальное значение размера проданного костюма. Решение. Из таблицы видно, что частота 52-го размера проданного костюма равна 29 и она является наибольшей. Следовательно, мода М0=52. Задача 8. Товарооборот магазина по месяцам составил (в тыс. руб.): 50; 53; 60; 52; 54; 48; 44,5; 62; 55; 53,5; 58, 64. Определить медиану и размах товарооборота. Решение. Расположив месячные товарообороты в порядке их возрастания, получим ряд: 44,5; 48; 50; 52; 53; 53,5; 54; 55; 58; 60; 62; 64. В этом вариационном ряде четное число данных и значения признака различны, поэтому по формуле (9.18) Ме =
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 829; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 , (9.7)
, (9.7) (среднее квадратов значений признака), а
(среднее квадратов значений признака), а  (средняя выборочная).
(средняя выборочная). и ДВ в случае интервальной выборки за х i в формулах (9.3) - (9.7) принимают значения х i * - середины интервалов.
и ДВ в случае интервальной выборки за х i в формулах (9.3) - (9.7) принимают значения х i * - середины интервалов. . (9.8)
. (9.8) определяется по формуле
определяется по формуле . (9.9)
. (9.9) . (9.10)
. (9.10) ,
, порядка k определяются по формуле
порядка k определяются по формуле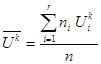 . (9.11)
. (9.11) h + c, (9.12)
h + c, (9.12) ]h2. (9.13)
]h2. (9.13) . (9.15)
. (9.15)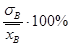 . (9.16)
. (9.16)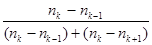 . (9.17)
. (9.17) . (9.18)
. (9.18) , где квадратные скобки показывают, что от числа
, где квадратные скобки показывают, что от числа 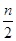 нужно взять только целую часть.
нужно взять только целую часть.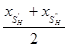 , (9.20)
, (9.20) - первое значение признака, для которого накопленная частота
- первое значение признака, для которого накопленная частота  не менее
не менее  - первое значение признака, для которого накопленная частота
- первое значение признака, для которого накопленная частота  не менее
не менее 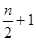 .
. . Этот интервал называется медианным. Величину медианы определяют по формуле
. Этот интервал называется медианным. Величину медианы определяют по формуле , (9.21)
, (9.21) , (9.22)
, (9.22) , (9.23)
, (9.23) ni
ni 9
9 7
7



 Wi
Wi 0 х
0 х . Гистограмма частот изображена на рисунке ниже.
. Гистограмма частот изображена на рисунке ниже.





 0 90 100 110 120 130 140 150 160 х
0 90 100 110 120 130 140 150 160 х
 , где Wi – относительные частоты соответствующих частичных промежутков. Изображение гистограммы относительных частот см. на рисунке.
, где Wi – относительные частоты соответствующих частичных промежутков. Изображение гистограммы относительных частот см. на рисунке.
 при 35< х £ 36. Значения Х <37 (х 1=35, х 2=36) наблюдались 4+5=9 раз. Следовательно, F*(х)=
при 35< х £ 36. Значения Х <37 (х 1=35, х 2=36) наблюдались 4+5=9 раз. Следовательно, F*(х)=  при 36< х £ 37. Аналогично находим: F*(х) =
при 36< х £ 37. Аналогично находим: F*(х) =  при 37< x £ 38; F*(х) =
при 37< x £ 38; F*(х) = 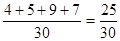 при 38< х £ 39; F*(х) =
при 38< х £ 39; F*(х) =  при 39< х £ 40. Так как х =40 – наибольшая варианта, то F*(х)=1 при х >40. Запишем эмпирическую функцию:
при 39< х £ 40. Так как х =40 – наибольшая варианта, то F*(х)=1 при х >40. Запишем эмпирическую функцию:
 y
y
 (ц).
(ц).
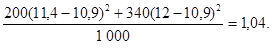
 » 1,02.
» 1,02.

 »73,5.
»73,5. .
.
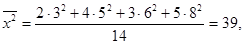

 m3=
m3= 





