
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычислим размах товарооборота по формуле (9.14). Получим, чтоСодержание книги
Поиск на нашем сайте
R = 64 - 44,5 = 19,5. Задача 9. Пусть дан статистический ряд
Решение. Для этого ряда n=2+5+12+8+6+5=47, т.е. нечетное число. Для нечетного n с повторяющимися х i, медиана соответствует значению признака Х, имеющего накопленную частоту SH= Задача 10. Определить медиану следующего статистического ряда:
Решение. Для этого ряда n=8+12+12+14+10+14+10+20=100, т.е. четное число. Первое значение признака Х, для которого накопленная частота равна или больше 50, будет Ме = Задача 11. Обследование выполнения годового плана на предприятиях города дало следующие результаты (в процентах):
Найти медиану данного интервального статистического распределения. Решение. Находим общее количество предприятий города: n = 3+8+12+20+10+6+1 = 60. Четвертый интервал (105-110) является медианным интервалом. По формуле (9.21) находим медиану: Ме = 105 + Задача 12. По результатам опроса 60 работников завода о величине месячного душевого дохода были получены следующие данные:
Вычислить асимметрию и эксцесс распределения. Решение. Для вычисления асимметрии и эксцесса предварительно находим
ДВ= sВ = m3= m4= По формулам (9.22) и (9.23) получим следующие результаты: a = e =
З а д а ч и
1. Составить статистический закон распределения варианты Х – размера мужской обуви, проданной магазином за день в такой последовательности: 40, 42, 44, 41, 43, 44, 40, 41, 43, 43, 44, 43, 41, 40, 43, 43, 44, 44, 44, 43, 42, 42, 41, 43, 41, 43, 44, 44, 43, 42, 41, 40, 43, 42, 41, 44, 43, 42, 43, 44, 41, 43, 42, 43, 44, 41, 42, 43, 44, 43, 42, 44, 43, 42, 43, 44, 43, 41, 40, 44. Построить полигоны частот и относительных частот. 2. Распределение мигрировавшего городского населения области дано таблицей
Построить гистограмму численности прибытия и выбытия населения области. 3. Найти эмпирическую функцию распределения по заданным выборкам:
Построить графики этих функций. 4. В райторге имеется 20 магазинов, из которых 7 реализовали товаров на 40 000 руб.; 9 – на 50 000 руб. и 4 магазина – на 45 000 руб. каждый. Найдите выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение товарооборота магазинов торга. Поясните экономический смысл этих величин. 5. Распределение месячной выработки однотипных деталей рабочими цеха задано таблицей
Определить среднюю месячную выработку рабочего цеха и среднее квадратическое отклонение. 6. Распределение 50 складов по складскому обороту задано следующей таблицей:
Найти коэффициент вариации. 7. Вычислить начальные и центральные моменты первого, второго, третьего и четвертого порядка по заданному статистическому распределению:
8. Дневная выработка 100 рабочих, занятых на изготовлении деталей, задана статистическим рядом
Требуется найти медиану распределения. 9. Итоги сдачи экзамена по теории вероятностей и математической статистике студентами второго курса представлены таблицей:
Вычислить: 1) среднюю оценку, полученную на экзамене; 2) среднее квадратическое отклонение; 3) моду; 4) медиану; 5) размах варьирования; 6)коэффициент вариации; 7) асимметрию; 8) эксцесс; 9) среднее абсолютное отклонение. 10. Найти выборочную среднюю и выборочную дисперсию методом произведений по следующему статистическому распределению:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.181.112 (0.008 с.) |

 Найти медиану этого ряда.
Найти медиану этого ряда. Первое значение признака Х, имеющего накопленную частоту, равную или большую 24, будет х =26, т.к. ему соответствует накопленная частота SH=2+5+9+12=28. Следовательно, Ме=26.
Первое значение признака Х, имеющего накопленную частоту, равную или большую 24, будет х =26, т.к. ему соответствует накопленная частота SH=2+5+9+12=28. Следовательно, Ме=26. А первое значение признака Х, для которого накопленная частота равна или больше 51, будет
А первое значение признака Х, для которого накопленная частота равна или больше 51, будет  По формуле (9.20) определим медиану:
По формуле (9.20) определим медиану:

 , ДВ, sВ и центральные моменты 3-го и 4-го порядков. Получим
, ДВ, sВ и центральные моменты 3-го и 4-го порядков. Получим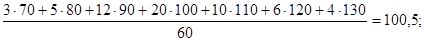
 214,63;
214,63;
 127,75;
127,75; 126 722,3 125.
126 722,3 125.




