
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Повторение испытаний. Схема Бернулли. Биномиальное распределение. Формула ПуассонаСодержание книги
Поиск на нашем сайте
Последовательные испытания наз-ся независимыми, если вероятность осущ-я любого исхода в n-ом по счету эксперименте не зависит от исходов предыдущих испытаний. Схема испытаний Бернулли: 1. послед-ть независимых испытаний с двумя исходами («успех» и «неуспех»); 2. эксперимент проводится n раз в неизменных усл-ях, т.е. вероятности «успеха»(p) и «неуспеха»(1-p=q) неизменны.
n-число испытаний, k-число благоприятных исходов, событие А – «успех», Х – случ.величина, обозначающая число «успехов» в n испытаниях по сх. Бернулли (Х=0,1,2,…n).
Соответствующее распр-е случ.вел.Х наз-ся биномиальным распр-ем. Свойства бином.распр-я: 1. 2. 3. Приближенная формула Пуассона: · 9.Производящие функции вероятностей. · G(z)=P0+P1z+P2z+…+Pkzk…=M[zk] · G(1)= (кси) =1 · G’(z)=P1+2P2z+3P3z2+…+ KPKzk-1 · G’(1)=M[x]=m · G”(z)=2P2+6P3z+…+k(k-1)PkZk-2 · G”(1)=∑k2Pk - ∑kPk · k=0 k=0 Биномиальное распределение · X=0,1,2,…n –бином-ое распредел. · Pk=P[x=k]=CknPkqn-k · G(z)=P0+P1z+P2z+…+Pkzk…=∑ CknPkqn-kzk= · =∑ Ckn(pz)kqn-k=(pz+q)n · G’(z)=n(pz+q)n-1p · G’(1)=M[x]=np · G”(z)=n(n-1)(pz+q)n-2p2 · G”(1)=n(n-1)p2 · M[x]=np = ∑kPk D[x]=npq = ∑(k-np)2Pk · Распределение Пуассона · Pk=P[x=k]= (λk\k!)e-λ · G(z)= ∑(λk\k!)e-λzk=e-λ∑(λz)k\k!= e-λ ezλ= eλ(z-1) · G’(1)= eλ(z-1) λ · G’(1)= λ= M[x]=m · G”(z)= eλ(z-1) λ2 · G”(1)= λ2 · M[x]=λ D[x]= λ2+ λ- λ2= λ · Геометрическое распределение · X=0,1,2…. · Pk=P[x=k]qkp · G(z)= ∑Pkzk=∑qkpzk=p∑(qz)k=P*1\(1-qz)=P\(1-qz) · M[x]=1\p D[x]=q\p2 · 10.Вероятность в непрерывных пространствах элементарных событий и ее свойства. Геометрические вероятности · Пусть · Алгебра событий (F) – это система подмножеств · 1. · 2. A,B · 3 · Пусть событие А · 1. · 2. · 3. · 4. P(A+B)<=P(A)+P(B) · 5. непрерывности: · если А1, А2,…, Аn,…: · если · Геометрические вер-ти, Для любого подмножества А можно посчитать его площадь: Р(А)=площ.А/площ. · Т.к. вер-ть пропорцион-на площади, то чем > лощадь, тем > вероятность попадания в событие. · P(A)=mes(A)/mes(
11.Непрерывные случайные величины. Функция распределения и плотность распределения, и их Свойства. Механическая интерпретация. Свойства мат. Ожидания и дисперсии. Квантили. Мода. Медиана. Асимметрия и эксцесс Случайная величина Х называется непрерывной, если для нее существует неотрицательная частично-непрерывная функция f(x), удовлетворяющая для любых значений x равенству
F(x) – ф-я распределения для непрер.случ.величин, определена на всей числовой оси, ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х. Свойства: 1. 2. F(- 3. F(+ 4. F(X)-неубыв.ф-я 5. 6. F(X)=dF(X)/dx 7. Мат.ожидание: 1. M[cX]=cM[X] 2. M[c+X]=c+M[X] 3. M[X+Y]=M[X]+M[Y] 4. = Дисперсия: Центральный момент k-го порядка - Эксцесс –
Нормальное распределение. Вероятность попадания в интервал, симметричный относительно мат. ожидания. Асимметрия и эксцесс распределения. Вычисление центрального момента порядка k. Стандартизированное нормальное распределение и его свойство. Правило трех сигм. Нормальное распределение N(m,s2) имеет плотность, определяемую формулой:
Функция распр-я F(х) норм.распр-я равна:
Параметры m и s2 норм.распр-я равны соответственно мат.ожиданию и дисперсии случ.вел-ны Х:
Центральные моменты норм.распр-я можно вычислить из рекуррентного ур-ния: μk+2=(k+1)s2μk, k=0,1,2,… (причем μ0=1) Для норм.распр-я все центр.моменты нечетного порядка равны 0. Коэффициент ассиметрии ax норм.распр-я равен 0. ax=μ3/s3 Из формул получаем: μ2=s2, μ4=3s4 Коэффициент эксцесса равен 0: ех= μ4/s4-3=0 Стандартизированное нормальное распределение и его свойство. Норм.распр-е с нулевым мат.ожиданием и дисперсией,равной 1, назыв.стандартным норм.распр-нием: Х~ N(0,1) Ф-ла плотности j(х) станд.норм.закона равна
А функция распр-я:
Так как плотность распр-я станд.норм.закона j(х) симметрична относ-но оси ординат,то для ф-ции распр-я Ф(х) справедливо след.св-во: Ф(-х)=1-Ф(х) Зн-я функции Ф(х) использ.при вычислении вер-ти попадания норм.распр-ной случ.величины Х в заданный интервал:
В практич.задач часто приходится вычислять вер-ть попадания случайной величины Х~ N(m,s2) в интервал, симметричный относительно ее математического ожидания m:
Используя получ.рез-тат,вычислим вер-ть отклоенения от мат.ожидания норма.распр-ной случ.вел-ны на вел-ну,равную трем средневкадратич.отклонениям, 3s: P[|X-m|<3s]=2Ф(3)-1»2*0,9987-1»0,9973 Этот результат известен как «правило трех сигм»: с вер-тью 0,9974(практически =1)зн-е нормально распределенной случ.вел-ны лежит в интервале (m-3s;m+3s) Правило трех сигм это правило часто используется для подтверждения или отбрасывания гипотезы о нормальном распределении случайной величины.
Системы дискретных случайных величин. Таблица распределения. Независимость. Ковариация. Механическая интерпретация. Условные распределения. Рассмотрим две случайные величины X и Y, определенные на одном дискретном вероятностном пр-ве (Ω,F,P). Обозначим значения, кот. принимает случ. величина Х через х1, х2, …, хn, а значения случ. величины Y через y1,y2,…,yn. Распределение вероятностей X и Y обозначим соответственно pх1, pх2, …, pхn и py1, py2, …, pyn. Вер-ть события, состоящего в том, что Х=хi и Y=yj, обозначим как P[X=xi; Y=yj]=pij. Опр Система равенств P[X=xi; Y=yj]=pij, pij>0, Распределение системы 2-ух дискр. случ. вел. (X,Y) записывают в виде таблицы распределения.
Таблица (1) Суммируя вер-ти pij по строкам, получим рапределение случ. вел X: Условные распределения: Условная вер-ть события Х=хi при условии, что Y=yj (pyi>0) определяется формулой Опр Определение независимости случ. величин. Пусть таблица (1) суть таблица распределения случ. вел X и Y. Случ. вел-ны X и Y наз. независимыми, если события X=xi и Y=yj независимы для всех i и j таких, что 1≤i≤n, 1≤j≤m, т.е. Опр Случайные величины X1, X2,..,Xn определенные на одном дискретном вероятностном пр-ве наз. взаимно независимыми, если для любой комбинации значений xi1, xi2,.., xin. Опр П усть случ. величины X и Yимеют конечные дисперсии. Ковариацией X и Y наз.. математическое ожидание произведения центрированных случ. величин (X-mx) и (Y-my): cov(X,Y)=M[(X-mx)(Y-my)]= Св-ва cov: 1.Если X и Y независимые случ. вел, то cov(X,Y)=0, обратное же неверное, т.е. если cov(X,Y)=0, это не значит,что величины независимы. 2.cov(aX,aY)=abcov(X,Y), где a и b – константы 3.cov(X,Y)≤ Это неравенство явл. следствием неравенства Коши-Буняковского: (M[XY])2≤M[X2]*M[Y2] (1). Док-во нер-ва (1): Рассмотрим очевидное неравенство M[(aX+Y)2] ≥0, где а-любое действительное число, а≠0. Преобразуем левую часть этого неравенства, используя св-ва мат. ожиданий M[(aX+Y)2]=M[a2X2+2aXY+Y2]=a2M[X2]+2aM[XY]+M[Y2]≥0 Т. К. Полученный относительно a трехчлен принимает только неотрицательные значения, то его дискриминант будет меньше или равен нулю: 4(M[XY])2-4M[X2] *M[Y2]≤0 Отсюда следует неравенство (M[XY])2≤M[X2]*M[Y2]. Заменим X на (X-mx), а Y на (Y-my), получим: (M[(X-mx)(Y-my)])2≤M[(X-mx)2]*M[(Y-my)2] или (cov(X,Y))2≤D[X]*D[Y] Механическая интерпретация.
N-мерные случ. величины (x1, x2,..,xn)- n-мерный случ. вектор (x1, x2,..,xn)= M[ Cov(Xi;Yj)=M[(Xi-mxi)(Yj-myj)], j,i=1,..,n
D[x1+x2+x3]=D[x1]+D[x2]+D[x3]+2cov(x1,x2)+2cov(x2,x3)+2cov(x1,x3)
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.37.211 (0.007 с.) |

 - формула Бернулли, где Cnk-число случайного размещения события А в послед-ти из n мест.
- формула Бернулли, где Cnk-число случайного размещения события А в послед-ти из n мест. ;
; -матем.ожидание
-матем.ожидание -дисперсия.
-дисперсия.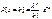 . При
. При  ,
,  при условии
при условии  (-интенсивность потока):
(-интенсивность потока): 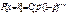 =
=  =
=  ;
;  .
. - непрерывное простр-во.
- непрерывное простр-во. , кот.удовл-ет следующим свойствам:
, кот.удовл-ет следующим свойствам: ;
; F => A+B
F => A+B  . F явл-ся сигма-алгеброй, если определены операции.
. F явл-ся сигма-алгеброй, если определены операции. - вер-ть невозможного события
- вер-ть невозможного события
 - если А-следствие В, то Р(А)<=Р(В).
- если А-следствие В, то Р(А)<=Р(В). , то
, то  ;
; , то
, то  .
.
 (случайные величины, возможные значения которых образуют некоторый интервал). fx - плотность распределения вероятностей (плотность распр-я единичной массы на инт-ле). Св-ва:
(случайные величины, возможные значения которых образуют некоторый интервал). fx - плотность распределения вероятностей (плотность распр-я единичной массы на инт-ле). Св-ва: если x
если x  ;
;  ;
; 
 если
если  : 1. f(x)>=0; 2.
: 1. f(x)>=0; 2.  ;
;  - норм.распр-е.
- норм.распр-е. 0 <=F(X)<= 1
0 <=F(X)<= 1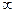 )=0
)=0
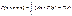 - вер-ть попадания в отрезок [c;d].
- вер-ть попадания в отрезок [c;d]. ,
,  , где f(x)dx=P[x<X<x+dx] – элемент вер-ти. Свойства:
, где f(x)dx=P[x<X<x+dx] – элемент вер-ти. Свойства: ,
, 
 ,
,  . Начальный момент k-го порядка -
. Начальный момент k-го порядка -  ;
; . Асимметрия -
. Асимметрия -  , где
, где  - ср.квадратич.отклонение
- ср.квадратич.отклонение хар-ет форму распред-я в окрестности вершины
хар-ет форму распред-я в окрестности вершины Квантиль – абсцисса (точка на оси х), которая слева от себя отделяет площадь под графиком плотности, равную Р. F(xp)=P – порядок квантили. 1.
Квантиль – абсцисса (точка на оси х), которая слева от себя отделяет площадь под графиком плотности, равную Р. F(xp)=P – порядок квантили. 1.  ; 2.
; 2. 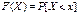 . Квантиль порядка 0,5 – х0,5 – для любого распр-я наз-ся медианой (h) (отделяет ½ площади под плотностью слева и справа). Если распр-е симметрично, то h совпадает с мат.ож. m.
. Квантиль порядка 0,5 – х0,5 – для любого распр-я наз-ся медианой (h) (отделяет ½ площади под плотностью слева и справа). Если распр-е симметрично, то h совпадает с мат.ож. m.
 Мода (d) – абсцисса, при кот. плотность распр-я имеет максимум: f(d)=max
Мода (d) – абсцисса, при кот. плотность распр-я имеет максимум: f(d)=max - моды нет (несколько лок.максимумов)
- моды нет (несколько лок.максимумов)
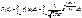


 , -¥<x<¥
, -¥<x<¥


 , pij=1, i=1,2,.., n, j=1,2,..,m определяет совместное распределение дискретных случайных величин X и Y или системы 2-ух дискр. случ. величин (X,Y).
, pij=1, i=1,2,.., n, j=1,2,..,m определяет совместное распределение дискретных случайных величин X и Y или системы 2-ух дискр. случ. величин (X,Y). , i=1,2,.., n, суммирование вер-тей pij по столбцам дает распределение случ. вел. Y:
, i=1,2,.., n, суммирование вер-тей pij по столбцам дает распределение случ. вел. Y:  , j=1,2,..,m. Аналогично определяется распределение системы более чем 2-ух случ. вел.
, j=1,2,..,m. Аналогично определяется распределение системы более чем 2-ух случ. вел.
 (1). Система равенств (1) при, i=1,2,.., n задает условное распределение случ. вел. X при условии,что случ. вел Y принимает заданное значение Y= yj.
(1). Система равенств (1) при, i=1,2,.., n задает условное распределение случ. вел. X при условии,что случ. вел Y принимает заданное значение Y= yj. или pij=
или pij=  .(если это условие не выполняется, то величины зависимые) Если X и Y независимые случ. вел., то таблица распределения (1) имеет вид таблицы умножения. Аналогично определяется взаимная независимость более чем 2-ух случ. вел. Для независ. случ. вел. Условные вер-ти равны безусловным вер-тям
.(если это условие не выполняется, то величины зависимые) Если X и Y независимые случ. вел., то таблица распределения (1) имеет вид таблицы умножения. Аналогично определяется взаимная независимость более чем 2-ух случ. вел. Для независ. случ. вел. Условные вер-ти равны безусловным вер-тям  =
=  ,
, 

 .
. M[XY]-mxM[Y]-mxM[X]+mxmy=M[XY]-mxmy (Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от её математического ожидания)
M[XY]-mxM[Y]-mxM[X]+mxmy=M[XY]-mxmy (Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от её математического ожидания)


 -ковариационная матрица (симметрична)
-ковариационная матрица (симметрична)
 -корреляционная матрица(симметрична)
-корреляционная матрица(симметрична)


