
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доверит.инт.для разности среднихСодержание книги
Поиск на нашем сайте Если дов.инт для m1-m2 содержит в себе 0, то различие 2х совокупн.незначимо и вызвано случайной изменчивостью величин и ошибкой измерений.
1.есть: N(m, n1\X1 n2\X2 (X c чертой) σ^2 известны.
рассуждая так же,как и для дов.инт для среднего с ИЗВЕСТНОЙ дисперсией: ( 2.Если Дисперсия НЕИЗВЕСТНА,то можно считать,что
S2несмещ оц.дисперсии σ2 использ стат Y= (
Проверка стат.гипотез. Классиф. Критерий. Стат.крит. Ур-нь значимости. Крит.обл. Ошибки 1 и 2 рода. Пусть Х – наблюдаемая СВ. Она может быть дискретной, а может и непрерывной. Статич.гипотеза Н-предположение относительно параметров или вида распределения СВ Х. -простая –однозначно определ.распр СВ Х -сложная -параметрич-распр Х известно,но необходд.проверить предполож. о значениях парам-в распредел. Проверяемая гипотеза -нулевая гип.-Н0. Обязательно на ряду с Н0 рассматривают одну из альтернативных гипотез Н1. При этом имеются различные ситуации для Н1.
Выбор альтернативной гипотезы Н1 определяется конкретной формулировкой задачи Критерий-правило,по кот.проверяют гипотезу Так как решение принимается на основе выборки наблюдений СВ Х, то необходимо выбрать подходящую статистику, которую мы будем называть статистикой Z критерия К. Замечание. При проверке простой параметрической гипотезы Н0: q=q0 в качестве статистики критерия выбирают ту же статистику, что и для оценки параметра q, т.е. Основной принцип при проверке статистической гипотезы: Маловероятные события считаются невозможными, а события, имеющие большую вероятность, считаются достоверными. Реализация этого принципа на практике. Перед анализом выборки фиксируется некоторая малая вероятность a, называемая уровнем значимости. Пусть V множества значений статистики Z, VK – подмножество множества значений статистики Z (VK £ V). Это такое подмножество, что при условии истинности гипотезы Н0, имеем вероятность того, что P{ZÎVkïH0}=a. Обозначим через z в – выборочное значение статистики Z, которое вычитается по конкретной выборке. Критерии К формулируется следующим образом. Отклонить гипотезу Н0, если zвÎVk. Отклонить гипотезу Н0, если zвÎV \ Vk. Уровень значимости a определяет размер критической области, а ее положение зависит от альтернативной гипотезы Н1.
Z1–a– квантиль распределения Z при условии, что верна гипотеза Н0.
Za– квантиль распределения Z при условии, что верна гипотеза Н0.
Проверку параметрической гипотезы при помощи критерия значимости можно разбить на следующие этапы:1)сформулировать Н0 и Н1;2)назначить a;3)выбрать статистику Z для проверки Н0;4)определить выборочное распределение Z при условии, что верна Н0;5)определить VK (она зависит от Н1);6)получить выборку и вычислить zb;7)принять статистическое решение: zвÎVk – отклонить Н0; zвÎV \Vk – принять Н0. Ошибка 1ого рода: если Но отклонена,но она верна. Вероятность P{ZÎVkïH0}=a.. -вер-ть попадания статистики Z в крит. область Vk,при усл что Но верна= Ошибка 2ого рода: гип. Но принимается, но верна гипотеза Н1(приняли неверную гипотезу) Вероятность ошибки второго рода при условии, что гипотеза Н1 – простая, P{ZÎV\VkïH1}=b. Проверка гипотез с использованием критерия значимости может быть проведена на основе доверительных интервалов. При этом одностороннему критерию значимости будет соответствовать односторонний доверительный интервал, а двустороннему критерию значимости будет соответствовать, двусторонний доверительный интервал. Гипотеза Н0 – принимается, если значение q0 накрывается доверительным интервалом, иначе отклоняется.
Проверка гипотез о равенстве дисперсий и средних.
4)так как выборка получена из нормально распределенной генеральной совокупности, выборочное среднее также имеет нормальное распределение с дисперсией
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 ) N(m,
) N(m, 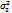 )
) и статитика Y=
и статитика Y=  ~N(0,1)
~N(0,1)

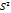 =
=  S12-несмещ.оц дисп. определенная по выборке n1; S22-несмещ.оц дисп. определенная по выб. n2
S12-несмещ.оц дисп. определенная по выборке n1; S22-несмещ.оц дисп. определенная по выб. n2 ~T(n1+n2-2)-степенями свободы,получ довер инт:
~T(n1+n2-2)-степенями свободы,получ довер инт:
 ;
;  ;
;  ;
;  .
.

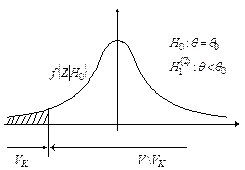



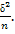 При условии, что верна гипотеза Н0, мат. ожидание этого распределения равно 10. Нормированная статистика
При условии, что верна гипотеза Н0, мат. ожидание этого распределения равно 10. Нормированная статистика  имеет нормальное распределение N (0,1).
имеет нормальное распределение N (0,1).





