
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные события. Пространство элементарных событий. Алгебра событий.Содержание книги
Поиск на нашем сайте Случайные события. Пространство элементарных событий. Алгебра событий. Влияние случ.факторов приводит к тому,что мы постоянно получаем разл.значен-я(пр измерении каких-либо предметов) Случайные соб-я – это события,которые могут произойти,а могут и не произойти. Серия экспериментов- последов-ть экспериментов,проводимых в неизменных условиях. А-случ.соб-е n раз повторяется эксперимент. nA –частота появления соб.А в n экспериментах. Относит.частота hA= nA/n – статистич.опр-е(отношение числа экспериментов А к числу всех благопр.исходов) Р(А)-вер-ть соб.А. Такая процедура назыв.частотное определение вер-ти соб.А Пространство элемент.соб-тий Пример. Подбрасывание игр.кости 1 раз. w1-выпала «1», w2- выпала «2»... w6-выпала «6» Соб.А –выпад.четного числа очков. А={ w2; w4; w6 } Соб.В-вып.числа очков кратных 3. В={ w3; w6 } Множество W всех элемент.исходов данного эксперимента назыв. пространством элементарных событий. W={ w1; w2... } Операции над случ.событиями: д иаграмма Эйлер-Венна А) событие A Б) Суммой событий А и В назыв.соб. А+В,состоящее из элемент.соб, принадлежащ.хотя бы одному из соб.А или В. В) Произведением событий А и B назыв.соб. АВ,сост.из элемент.соб-й,принадлеж.одновременно А и В. Г) Разностью соб.А иВ назыв.соб-е А-В,сост.из элем.соб-й,принадлежащих А и не принадлеж.В. Д) Соб.Ā=w/А назыв. противоположным событию A(или дополн.к соб.А) Е) Несовместимые события (если они не могут произойти одноременно), если АВ=Æ Ж) События образуют полную группу, если хотя бы одно из них обязательно происходит в результате испытания. З) Если из наступления соб.А следует наступл.В,т.е соб.В есть следствие А,то это записыв.так: АÌВ. Алгебра событий: Система F подмножеств W,удовлетворяющая условиям: 1)WÎF; 2) из того,что А,ВÎF,следует,что А+ВÎF, ABÎF, Ā,B(с черточкой)ÎF называется алгеброй событий. Т. о., алгебра F-это система подмножеств W,котор.замкнута относ-но конечного числа опер-й слож-я, умн-я и доп-я. Если усл-е 2) выполн.для счетного числа соб-й,то алгебра F называется s-алгеброй(сигма-алгеброй)
Вероятность в дискретных пространствах элементарных событий. Пусть W содержит либо конечное, либо счетное число элемнт.соб-й: W={w1,w2,..} F-набор все подмножеств W. F явл. s-алгебра. Каждому эл.исходу wi (i=1,2,..) поставим в соот-е неотриц.число P(wi)=pi, такое что å pi=1 и 0≤pi≤1. Следствия: P(A)=å p(wi), 0≤P(A)≤1, P(W)=1, P(Æ)=0, P(Ā)=1-P(A), P(A+B)≤P(A)+P(B) или P(A+B)+P(A)+P(B)-P(AB) Вероятностное прост-во (W,F,P) называется в этом случае дискретным. Классическая схема равновероятных событий. Если W сожержит конечное число эл.соб-й,например N соб-й, причем все эл.исходы равновозможны,т.е. p(wi)=1/N, i-1,2,..,N, то P(A)=|A|/|W|, где |A|-кол-во эл.исходы,составляющих множество А, а |W|- число всех эл.исходов данного эксперимента. |W|=N Такая ф-ла назыв. классическим определением вер-ти (Если эл.исходы равновозможны, то вер-ть соб.А равна отношению числа исходов,благоприятствующих соб.А, к числу всех эл.исходов) Теорема сложения и умножения вероятности.
усл.вер-ть P(A/B) усл.вер-ть P(B/A)
-теорема умножения для зависимых соб.А и В.
Если соб.А не влияет на вер-ть соб.В и наоборот,то они независимы: P(A/B)=P(A); P(B)=P(B/A) => P(AB)+P(A)*P(B) – вер-ть произ-ния соб-й равна произ-нию вер-тей. P(ABC)=P(AH)*P(A/H)=P(BC)*P(A/BC)=P(C)*P(B/C)*P(A/BC) (ВС обозначили за Н) Опр-е независимости для А,В и С- соб. А,В и С назыв.независимыми в совокупности,если выполн.след усл-я: 1) Если попарно независимы P(AB)=P(A)*P(B), P(BC)=P(B)*P(C), P(AC)=P(A)*P(C). 2) P(ABC)=P(A)*P(B)*P(C) P(A+B)=P(A)+P(B) вер-ть суммы двух несовместных событий
P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC) вер-ть суммы трех несовместных соб-й Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления. Формула полной вероятности и формула Байеса. Формула полной вероятности Пусть Н1,Н2…Нk подмножества пространства эл.соб-й W, такие что: 1) Hi Hj=Æ, i≠j и I,j=1,2,…,k 2) H1+H2+…+Hk = W В этом случае говоря,что сис-ма подмножеств Н1,Н2…Нk образует разбиение множества W. Для любого соб.А,являющего подмножеством W, верна ф-ла полной вер-ти P(A)= События Hi называются гипотезами по отношению к соб.А,а вер-ти Р (Hi) трактуются как доопытные вер-ти гипотез, причем å Р (Hi)=1. Формула Байеса Если известно, что соб.А произошло, то априорные(после опыта) вер-ти гипотез Hi,очевидно, должны быть пересчитаны, так как появилась доп.информация. Апостериорные вер-ти гипотез Hi,при условии, что соб.А произошло,вычисляются по ф-ле Байеса:
где Р(А) определяется по ф-ле полной вер-ти.
истор.процесса – локальная цивилизация – общность людей, объединенных дух.традициями и проживающие на одной тер-и. Выделяет первичные, вторичные и третичные цивилизации. Свыше 20 цив-ций. Сейчас основных 8 (западно-христ, православно-христ, иудейская, исламская, индуистская, дальневосточная, буддистская, конфуцианская). 4 этапа развития: генезис, рост, упадок и дезинтеграция. Недостатки: не принимает во внимание качественные различия хозяйственных систем в современном мире. - теория единой цивилизации - теория столкновения цивилизаций 6. Основные вопросы экономики и способы их решения различными экономическими системами: традиционной, административно-плановой, рыночной, смешанной. Основные черты,преимущества и недостатки экономических систем. Нормальное распределение. Вероятность попадания в интервал, симметричный относительно мат. ожидания. Асимметрия и эксцесс распределения. Вычисление центрального момента порядка k. Стандартизированное нормальное распределение и его свойство. Правило трех сигм. Нормальное распределение N(m,s2) имеет плотность, определяемую формулой:
Функция распр-я F(х) норм.распр-я равна:
Параметры m и s2 норм.распр-я равны соответственно мат.ожиданию и дисперсии случ.вел-ны Х:
Центральные моменты норм.распр-я можно вычислить из рекуррентного ур-ния: μk+2=(k+1)s2μk, k=0,1,2,… (причем μ0=1) Для норм.распр-я все центр.моменты нечетного порядка равны 0. Коэффициент ассиметрии ax норм.распр-я равен 0. ax=μ3/s3 Из формул получаем: μ2=s2, μ4=3s4 Коэффициент эксцесса равен 0: ех= μ4/s4-3=0 Стандартизированное нормальное распределение и его свойство. Норм.распр-е с нулевым мат.ожиданием и дисперсией,равной 1, назыв.стандартным норм.распр-нием: Х~ N(0,1) Ф-ла плотности j(х) станд.норм.закона равна
А функция распр-я:
Так как плотность распр-я станд.норм.закона j(х) симметрична относ-но оси ординат,то для ф-ции распр-я Ф(х) справедливо след.св-во: Ф(-х)=1-Ф(х) Зн-я функции Ф(х) использ.при вычислении вер-ти попадания норм.распр-ной случ.величины Х в заданный интервал:
В практич.задач часто приходится вычислять вер-ть попадания случайной величины Х~ N(m,s2) в интервал, симметричный относительно ее математического ожидания m:
Используя получ.рез-тат,вычислим вер-ть отклоенения от мат.ожидания норма.распр-ной случ.вел-ны на вел-ну,равную трем средневкадратич.отклонениям, 3s: P[|X-m|<3s]=2Ф(3)-1»2*0,9987-1»0,9973 Этот результат известен как «правило трех сигм»: с вер-тью 0,9974(практически =1)зн-е нормально распределенной случ.вел-ны лежит в интервале (m-3s;m+3s) Правило трех сигм это правило часто используется для подтверждения или отбрасывания гипотезы о нормальном распределении случайной величины.
Системы дискретных случайных величин. Таблица распределения. Независимость. Ковариация. Механическая интерпретация. Условные распределения. Рассмотрим две случайные величины X и Y, определенные на одном дискретном вероятностном пр-ве (Ω,F,P). Обозначим значения, кот. принимает случ. величина Х через х1, х2, …, хn, а значения случ. величины Y через y1,y2,…,yn. Распределение вероятностей X и Y обозначим соответственно pх1, pх2, …, pхn и py1, py2, …, pyn. Вер-ть события, состоящего в том, что Х=хi и Y=yj, обозначим как P[X=xi; Y=yj]=pij. Опр Система равенств P[X=xi; Y=yj]=pij, pij>0, Распределение системы 2-ух дискр. случ. вел. (X,Y) записывают в виде таблицы распределения.
Таблица (1) Суммируя вер-ти pij по строкам, получим рапределение случ. вел X: Условные распределения: Условная вер-ть события Х=хi при условии, что Y=yj (pyi>0) определяется формулой Опр Определение независимости случ. величин. Пусть таблица (1) суть таблица распределения случ. вел X и Y. Случ. вел-ны X и Y наз. независимыми, если события X=xi и Y=yj независимы для всех i и j таких, что 1≤i≤n, 1≤j≤m, т.е. Опр Случайные величины X1, X2,..,Xn определенные на одном дискретном вероятностном пр-ве наз. взаимно независимыми, если для любой комбинации значений xi1, xi2,.., xin. Опр П усть случ. величины X и Yимеют конечные дисперсии. Ковариацией X и Y наз.. математическое ожидание произведения центрированных случ. величин (X-mx) и (Y-my): cov(X,Y)=M[(X-mx)(Y-my)]= Св-ва cov: 1.Если X и Y независимые случ. вел, то cov(X,Y)=0, обратное же неверное, т.е. если cov(X,Y)=0, это не значит,что величины независимы. 2.cov(aX,aY)=abcov(X,Y), где a и b – константы 3.cov(X,Y)≤ Это неравенство явл. следствием неравенства Коши-Буняковского: (M[XY])2≤M[X2]*M[Y2] (1). Док-во нер-ва (1): Рассмотрим очевидное неравенство M[(aX+Y)2] ≥0, где а-любое действительное число, а≠0. Преобразуем левую часть этого неравенства, используя св-ва мат. ожиданий M[(aX+Y)2]=M[a2X2+2aXY+Y2]=a2M[X2]+2aM[XY]+M[Y2]≥0 Т. К. Полученный относительно a трехчлен принимает только неотрицательные значения, то его дискриминант будет меньше или равен нулю: 4(M[XY])2-4M[X2] *M[Y2]≤0 Отсюда следует неравенство (M[XY])2≤M[X2]*M[Y2]. Заменим X на (X-mx), а Y на (Y-my), получим: (M[(X-mx)(Y-my)])2≤M[(X-mx)2]*M[(Y-my)2] или (cov(X,Y))2≤D[X]*D[Y] Механическая интерпретация.
N-мерные случ. величины (x1, x2,..,xn)- n-мерный случ. вектор (x1, x2,..,xn)= M[ Cov(Xi;Yj)=M[(Xi-mxi)(Yj-myj)], j,i=1,..,n
D[x1+x2+x3]=D[x1]+D[x2]+D[x3]+2cov(x1,x2)+2cov(x2,x3)+2cov(x1,x3) Математическое ожидание y=φ(x) 1. Пусть X- дискрет случ. вел, тогда yn= φ(xn)
2.Пусть X –непрер. Случ. вел
Для вычисления числовых характеристик неслучайной ф-ции случайной величины не надо знать закона распределения зависящей от X случайной величины Y, а достаточно знать закон распределения случайного аргумента X. Математическое ожидание
Дисперсия
Св-ва мат. ожидания и дисперсии: 1. M[X+Y] = M[X] + M[Y] 2. M[X*Y] = M[X] * M[Y] 3. D[X+Y] = D[X] + D[Y]
Коэффициент ковариации
Св-ва мат. ожидания и дисперсии: 1. Если X и Y независимы, то Cov(X,Y) = 0 (обратное неверно!)
2. Cov(aX,bY) = ab*Cov(X,Y), где a и b – константы 3. Cov(X,Y)
Коэффициент корреляции
Св-ва мат. ожидания и дисперсии: 1. |ρ(X,Y)| ≤ 1, этот результат следует из свойства 3 для ковариации случайных величин X и Y. 2. Если Х и Y – независимые случайные величины, то ρ(X,Y) = 0 (по свойству 1 для ковариации) 3. Если X и Y связаны линейной функциональной зависимостью: Y=aX + b, где a и b – константы, а ≠ 0, то |ρ(X,Y)| = 1 Следствия ЦПТ. Теорема Муавра-Лапласа. Пусть Х – случайная величина, имеющая биномиальное распределение. (q=1-p; n испытаний) Х – число успехов в n испытаниях по схеме Бернулли Х=0…n
Введем величину Причем
X = X1 + … + Xn (они все независимы и имеют одинаковое распределение) M[X] = M[X1 + … + Xn] = M[X1] + … + M[Xn] = np D[X] = D[X1 + … + Xn] = D[X1] + … + D[Xn] = npq Следовательно: X
Теорема Муавра-Лапласа позволяет количественно оценить разброс события А в некотором эксперименте, который может повторятся n раз в неизменных условиях. Приблизительное значение p равно значению наблюдаемой относительной частоты появления события А в n экспериментах, причем, чем больше n тем выше относительная точность этого результата.
Теорема Бернулли.
Пусть А – случайный исход некоторого экспериментов, P(A)=p – вероятность этого исхода. Предположим, что эксперимент повторяется n раз в неизменных условиях (т.е. вероятность Р(А)=р не изменяется при повторении экспериментов). Тогда относительная частота появление события А при n -> ∞ сходится по вероятности к р:
где n – общее число исходов, m – число благоприятных исходов, p – вероятность появления случ. величины. Док-во: Пусть Вычислим математическое ожидание случайной величины M[Xi] = 1*p + 0*q = p И математическое ожидание их среднего арифметического:
Случайные величины
Теорема Бернулли дает математическое обоснование экспериментальным результатам, в которых наблюдается устойчивость частот при увеличении числа экспериментов. Устойчивость среднего арифметического можно объяснить тем, что случайное отклонения от среднего, неизбежные в каждом отдельном результате, в массе однородных результатов взаимно поглощаются, нивелируются, выравниваются. Вследствие этого средний результат
ктически перестает быть случайным и может быть предсказан достаточно точно.
Предмет мат статистики. Основные понятия: выборка, генеральная совокупность, статистики Распределение выборки, выборочные моменты. Математическая статистика – это наука, изучающая случайные явления посредством обработки и анализа результатов наблюдений и измерений. Первая задача математической статистики – указать способы получения, группировки и обработки статистических данных, собранных в результате наблюдений, специально поставленных опытов или произведённых измерений. Вторая задача математической статистики – разработка методов анализа статистических сведений в зависимости от целей исследования. Случайную величину Х будем называть генеральной совокупностью Х. Исходным материалом для изучения свойств генеральной совокупности Х являются статистические данные, т.е. значения, полученные в результате повторения случайного опыта (измерения случайной величины). Предполагается, что опыт может быть повторён сколько угодно раз в неизменных условиях. Это означает, что распределение случайной величины,, заданной на множестве исходов -го опыта, не зависит от и совпадает с распределением генеральной совокупности. Набор независимых в совокупности случайных величин, где соответствует -му опыту, называют случайной выборкой из генеральной совокупности. Распределение выборки - -распределение дискретной случайной величины, приеимающей значения x1..xn(среди кот.мб и совпадающие) с вер-ями 1\n при этом вер-ти для совпадающих значений складываются Выборочные моменты в математической статистике — это оценка теоретических моментов распределения на основе выборки. Пусть Выборочный момент порядка k — это случайная величина
Центральный выборочный момент порядка k — это случайная величина
где символ
Постановка задачи Задача статистического оценивания неизвестных параметров - одна из двух основных (наряду с задачей проверки статистических гипотез) задач математической статистики. Предположим, что имеется параметрическое семейство распределений вероятностей для простоты будем рассматривать распределение случайных величин и случай одного параметра). Здесь Различают два основных типа оценок: точечные оценки и доверительные интервалы. очечное оценивание - это вид статистического оценивания, при котором значение неизвестного параметра
значение которой будет рассматриваться в качестве приближения к неизвестному истинному значению Состоятельность Одно из самых очевидных требований к точечной оценке заключается в том, чтобы можно было ожидать достаточно хорошего приближения к истинному значению параметра при достаточно больших значениях объема выборки n. Это означает, что оценка если если имеет место сходимость по вероятности Несмещенность Оценка
Более слабым условием является асимптотическая несмещенность, которая означает, что математическое ожидание оценки сходится к истинному значению параметра с ростом объема выборки:
Несмещенность является рекомендуемым свойством оценок. Однако не следует слишком переоценивать его значимость. Чаще всего несмещенные оценки параметров существуют и тогда стараются рассматривать только их. Однако могут быть такие статистические задачи, в которых несмещенных оценок не существует. Наиболее известным примером является следующий: рассмотрим распределение Пуассона с параметром Эффективность (Несмещенные) оценки, для которых достигается эта нижняя граница (т.е. имеющие минимально возможную дисперсию), называются эффективными. Однако существование эффективной оценки есть довольно сильное требование на задачу, которое имеет место далеко не всегда.
Д.инт. для среднего ДИСПЕРСИЯ ИЗВЕСТНА Пусть
Статистика По таблице нормального распределения найдем квантили
Учитывая, что
ДИСПЕРСИЯ НЕИЗВЕСТНА
Пусть В литературе по статистике показано, что Y имеет распределение Стьюдента с n –1 степенью свободы По заданной доверительной вероятности
Случайные события. Пространство элементарных событий. Алгебра событий. Влияние случ.факторов приводит к тому,что мы постоянно получаем разл.значен-я(пр измерении каких-либо предметов) Случайные соб-я – это события,которые могут произойти,а могут и не произойти. Серия экспериментов- последов-ть экспериментов,проводимых в неизменных условиях. А-случ.соб-е n раз повторяется эксперимент. nA –частота появления соб.А в n экспериментах. Относит.частота hA= nA/n – статистич.опр-е(отношение числа экспериментов А к числу всех благопр.исходов) Р(А)-вер-ть соб.А. Такая процедура назыв.частотное определение вер-ти соб.А Пространство элемент.соб-тий Пример. Подбрасывание игр.кости 1 раз. w1-выпала «1», w2- выпала «2»... w6-выпала «6» Соб.А –выпад.четного числа очков. А={ w2; w4; w6 } Соб.В-вып.числа очков кратных 3. В={ w3; w6 } Множество W всех элемент.исходов данного эксперимента назыв. пространством элементарных событий. W={ w1; w2... } Операции над случ.событиями: д иаграмма Эйлер-Венна А) событие A Б) Суммой событий А и В назыв.соб. А+В,состоящее из элемент.соб, принадлежащ.хотя бы одному из соб.А или В. В) Произведением событий А и B назыв.соб. АВ,сост.из элемент.соб-й,принадлеж.одновременно А и В. Г) Разностью соб.А иВ назыв.соб-е А-В,сост.из элем.соб-й,принадлежащих А и не принадлеж.В. Д) Соб.Ā=w/А назыв. противоположным событию A(или дополн.к соб.А) Е) Несовместимые события (если они не могут произойти одноременно), если АВ=Æ Ж) События образуют полную группу, если хотя бы одно из них обязательно происходит в результате испытания. З) Если из наступления соб.А следует наступл.В,т.е соб.В есть следствие А,то это записыв.так: АÌВ. Алгебра событий: Система F подмножеств W,удовлетворяющая условиям: 1)WÎF; 2) из того,что А,ВÎF,следует,что А+ВÎF, ABÎF, Ā,B(с черточкой)ÎF называется алгеброй событий. Т. о., алгебра F-это система подмножеств W,котор.замкнута относ-но конечного числа опер-й слож-я, умн-я и доп-я. Если усл-е 2) выполн.для счетного числа соб-й,то алгебра F называется s-алгеброй(сигма-алгеброй)
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 381; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |

 P(A/B)- условная вероятность события A при условии, что соб.B произошло.
P(A/B)- условная вероятность события A при условии, что соб.B произошло. - ф-ла сложения вер-тей двух совместных событий
- ф-ла сложения вер-тей двух совместных событий
 ,i=1,2,…,k,
,i=1,2,…,k,
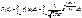


 , -¥<x<¥
, -¥<x<¥


 , pij=1, i=1,2,.., n, j=1,2,..,m определяет совместное распределение дискретных случайных величин X и Y или системы 2-ух дискр. случ. величин (X,Y).
, pij=1, i=1,2,.., n, j=1,2,..,m определяет совместное распределение дискретных случайных величин X и Y или системы 2-ух дискр. случ. величин (X,Y). , i=1,2,.., n, суммирование вер-тей pij по столбцам дает распределение случ. вел. Y:
, i=1,2,.., n, суммирование вер-тей pij по столбцам дает распределение случ. вел. Y:  , j=1,2,..,m. Аналогично определяется распределение системы более чем 2-ух случ. вел.
, j=1,2,..,m. Аналогично определяется распределение системы более чем 2-ух случ. вел.
 (1). Система равенств (1) при, i=1,2,.., n задает условное распределение случ. вел. X при условии,что случ. вел Y принимает заданное значение Y= yj.
(1). Система равенств (1) при, i=1,2,.., n задает условное распределение случ. вел. X при условии,что случ. вел Y принимает заданное значение Y= yj. или pij=
или pij=  .(если это условие не выполняется, то величины зависимые) Если X и Y независимые случ. вел., то таблица распределения (1) имеет вид таблицы умножения. Аналогично определяется взаимная независимость более чем 2-ух случ. вел. Для независ. случ. вел. Условные вер-ти равны безусловным вер-тям
.(если это условие не выполняется, то величины зависимые) Если X и Y независимые случ. вел., то таблица распределения (1) имеет вид таблицы умножения. Аналогично определяется взаимная независимость более чем 2-ух случ. вел. Для независ. случ. вел. Условные вер-ти равны безусловным вер-тям  =
=  ,
, 

 .
. M[XY]-mxM[Y]-mxM[X]+mxmy=M[XY]-mxmy (Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от её математического ожидания)
M[XY]-mxM[Y]-mxM[X]+mxmy=M[XY]-mxmy (Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от её математического ожидания)


 -ковариационная матрица (симметрична)
-ковариационная матрица (симметрична)
 -корреляционная матрица(симметрична)
-корреляционная матрица(симметрична)

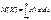











 M[Xi]=1*p+0*q=p
M[Xi]=1*p+0*q=p D[Xi]=M[Xi2]-p2=p-p2=p(1-p)=pq
D[Xi]=M[Xi2]-p2=p-p2=p(1-p)=pq

 , или
, или 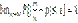
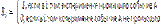 Причем
Причем  , а
, а  .
. :
:

 — выборка из распределения вероятности. Тогда
— выборка из распределения вероятности. Тогда

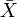 с чертой обозначает выборочное среднее.
с чертой обозначает выборочное среднее.
 - числовой параметр, значение которого неизвестно. Требуется оценить его по имеющейся выборке
- числовой параметр, значение которого неизвестно. Требуется оценить его по имеющейся выборке  значений, порожденной данным распределением.
значений, порожденной данным распределением. приближается отдельным числом. То есть необходимо указать функцию от выборки (статистику)
приближается отдельным числом. То есть необходимо указать функцию от выборки (статистику)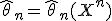
 должна сходиться к истинному значению
должна сходиться к истинному значению  . Это свойство оценки и называется состоятельностью. Поскольку речь идет о случайных величинах, для которых имеются разные виды сходимости, то и данное свойство может быть точно сформулировано по-разному:
. Это свойство оценки и называется состоятельностью. Поскольку речь идет о случайных величинах, для которых имеются разные виды сходимости, то и данное свойство может быть точно сформулировано по-разному: , то тогда оценка называется слабо состоятельной.
, то тогда оценка называется слабо состоятельной. .
.
 и поставим задачу оценки параметра
и поставим задачу оценки параметра  . Можно доказать, что для этой задачи не существует несмещенной оценки.
. Можно доказать, что для этой задачи не существует несмещенной оценки. – выборочный вектор n –наблюдений СВ Х, где
– выборочный вектор n –наблюдений СВ Х, где  . В качестве оценки для m возьмем
. В качестве оценки для m возьмем  . Предположим, что
. Предположим, что  известна. Рассмотрим статистику
известна. Рассмотрим статистику .
.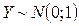 .
. и
и 
 .
. .
. .
. .
. .
. получаем
получаем .
. – выборочный вектор n –наблюдений СВ
– выборочный вектор n –наблюдений СВ  . В качестве оценки для m возьмем
. В качестве оценки для m возьмем  . Если дисперсия генеральной совокупности неизвестна, то по выборке определяем статистику
. Если дисперсия генеральной совокупности неизвестна, то по выборке определяем статистику  . Доверительный интервал для m в этом случае находится с помощью статистики
. Доверительный интервал для m в этом случае находится с помощью статистики 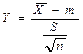 .
. .
.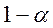 , используя таблицы распределения Стьюдента с n –1 степенью свободы, находим
, используя таблицы распределения Стьюдента с n –1 степенью свободы, находим  .
. .
. .
.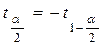
 .
.


