
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Чебышева и ее обобщение.Содержание книги
Поиск на нашем сайте
Если дисперсии n-независимых случайных величин (X1…Xn) ограничены одной и той же постоянной, то при неограниченном увеличении числа n среднее арифметическое случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий.
Док-во: По условию: M(
По первому неравенству Чебышева получаем:
поскольку P>1, то:
Вывод: при достаточно больших n выполнение рассматриваемого неравенства является событием практически достоверным, а неравенства противоположного смысла практически невозможно. Таким образом предел по вероятности следует понимать не как категорическое отверждение, а как утверждение, вероятность которого гарантируется с вероятностью близкой к 1 (при n->∞) Таким образом, при большом числе случайных величин практически достоверно, что их средняя случайная величина как угодна мало отличается от неслучаной – среднего математического ожидания, т.е. перестает быть случайной. Этим заключением обоснован выбор средней арифметической в качестве меры истинного значения мат. ожидания. Практическое значение: Пример: Необходимо установить размер страхового взноса, с условием что он(?) сделает выплаты при наступлении страхового случая. Замечание Если все измерения проводятся с одинаковой точностью и дисперсией (
Т.е. средний разброс случайной величины
Асимптотическое распределение среднего арифметического независимых случайных величин и относительной частоты.
Распределение среднего арифметического случайных величин. Пусть X1…Xn… - независимые и одинаково распределенные случайные величины с мат.ожиданием
При n->∞
Распределение относительно частоты Ћ = k/n – относительная частота появления события А, где k – число появлений события а в n испытаниях. 0,999 – (например) абсолютная частота
Ћ = k/n = X/n - число появлений события а в n испытаниях.
M[h] = M[X/n] = 1/n*np=p D[h] = D[X/n] = 1/n2*D[X]= 1/n2*npq=pq/n Ћ = k/n = X/n = X1/n + … + Xn/n Предмет мат статистики. Основные понятия: выборка, генеральная совокупность, статистики Распределение выборки, выборочные моменты. Математическая статистика – это наука, изучающая случайные явления посредством обработки и анализа результатов наблюдений и измерений. Первая задача математической статистики – указать способы получения, группировки и обработки статистических данных, собранных в результате наблюдений, специально поставленных опытов или произведённых измерений. Вторая задача математической статистики – разработка методов анализа статистических сведений в зависимости от целей исследования. Случайную величину Х будем называть генеральной совокупностью Х. Исходным материалом для изучения свойств генеральной совокупности Х являются статистические данные, т.е. значения, полученные в результате повторения случайного опыта (измерения случайной величины). Предполагается, что опыт может быть повторён сколько угодно раз в неизменных условиях. Это означает, что распределение случайной величины,, заданной на множестве исходов -го опыта, не зависит от и совпадает с распределением генеральной совокупности. Набор независимых в совокупности случайных величин, где соответствует -му опыту, называют случайной выборкой из генеральной совокупности. Распределение выборки - -распределение дискретной случайной величины, приеимающей значения x1..xn(среди кот.мб и совпадающие) с вер-ями 1\n при этом вер-ти для совпадающих значений складываются Выборочные моменты в математической статистике — это оценка теоретических моментов распределения на основе выборки. Пусть Выборочный момент порядка k — это случайная величина
Центральный выборочный момент порядка k — это случайная величина
где символ
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.248.17 (0.005 с.) |



 )=
)= 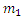 … M(
… M( )=
)= 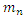


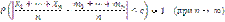
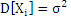 ), то дисперсия их средней величины
), то дисперсия их средней величины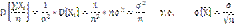
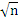 меньше разброса каждого измерения. Увеличивая число измерения можно уменьшить влияния случайных погрешностей (но не систематических)
меньше разброса каждого измерения. Увеличивая число измерения можно уменьшить влияния случайных погрешностей (но не систематических)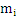 и дисперсией
и дисперсией 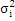 . Среднее арифметическое их:
. Среднее арифметическое их: 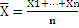
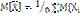 ]=nm/n=n
]=nm/n=n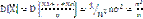 .
.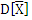 -> 0. Среднее арифметическое можно представить:
-> 0. Среднее арифметическое можно представить: 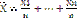 , т.е. можно рассмотреть как сумму случайных величин. Тогда
, т.е. можно рассмотреть как сумму случайных величин. Тогда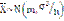 – в силу центральной предельной теоремы
– в силу центральной предельной теоремы
 — выборка из распределения вероятности. Тогда
— выборка из распределения вероятности. Тогда

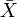 с чертой обозначает выборочное среднее.
с чертой обозначает выборочное среднее.


