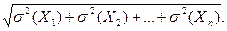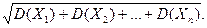Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсия числа появлений события в независимых испытанияхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А постоянна. Чему равна дисперсия числа появлений события в этих испытаниях? Ответ на этот вопрос дает следующая теорема. Теорема. Дисперсия числа появлений события А в п независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D (X) = npq. Доказательство. Рассмотрим случайную величину X — число появлений события А в п независимых испытаниях. Очевидно, общее число появлений события в этих испытаниях равно сумме появлений события в отдельных испытаниях: X = Х 1 + X 2 + …+ Хп, где Х 1— число наступлений события в первом испытании, Х 2— во втором,..., Хп — в п- м. Величины Х 1, Х 2,..., Хп взаимно независимы, так как исход каждого испытания не зависит от исходов остальных, поэтому мы вправе воспользоваться следствием 1 (см. § 5): D (X) = D (X 1) + D (X 2) +...+D (Хп). (*) Вычислим дисперсию X 1по формуле D (X 1) =M ( Величина Х 1—число появлений события А в первом испытании, поэтому (см. гл. VII, § 2, пример 2) М (Х 1) =р. Найдем математическое ожидание величины M ( Подставляя найденные результаты в соотношение (**), имеем D (X 1) =p-p 2 =p (1 -p) =pq Очевидно, дисперсия каждой из остальных случайных величин также равна pq. Заменив каждое слагаемое правой части (*) через pq, окончательно получим D (X) = npq. Замечание. Так как величина X распределена по биномиальному закону, то доказанную теорему можно сформулировать и так: дисперсия биномиального распределения с параметрами п и р равна произведению npq. Пример. Производятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины X —числа появлений события в этих испытаниях. Решение. По условию, n =10, р = 0,6. Очевидно, вероятность непоявления события q = 1 — 0, 6 = 0, 4. Искомая дисперсия D (X) = npq = 10 • 0, 6 • 0, 4 = 2, 4.
Среднее квадратическое отклонение
Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение. Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии: s (X)= Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то размерность s(X)совпадает сразмерностью X. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если X выражается влинейных метрах, то а (X)будет выражаться также влинейных метрах, a D (X)— в квадратных метрах. Пример. Случайная величина X задана законом распределения
Найти среднее квадратическое отклонение s(X). Решение. Найдем математическое ожидание X: М (Х) = 2 * 0, 1 + 3 * 0, 4 + 10 * 0, 5 = 6, 4. Найдем математическое ожидание X 2: М (Х 2) = 22 * 0, 1 + 32 * 0, 4 + 102 * 0, 5 = 54. Найдем дисперсию: D (X)= М (X 2) — [ М (X)]2 = 54 — 6, 42 = 13, 04. Искомое среднее квадратическое отклонение s (X)= Среднее квадратическое отклонение суммы взаимно независимых случайных величин
Пусть известны средние квадратические отклонения нескольких взаимно независимых случайных величин. Как найти среднее квадратическое отклонение суммы этих величин? Ответ на этот вопрос дает следующая теорема. Теорема. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин: s (X 1 +X 2 +…+Xn) = Доказательство. Обозначим через X сумму рассматриваемых взаимно независимых величин: X=X 1 +X 2 +…+Xn. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий слагаемых (см. § 5, следствие 1), поэтому D (X) = D (X 1) + D (X 2) +...+D (Xn). Отсюда
или окончательно s (X) =
|
||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 760; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.227.73 (0.007 с.) |

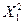 ) - [ M (X 1)]2. (**)
) - [ M (X 1)]2. (**)