
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мат. Ожидание и дисперсия суммы случайных величин. Мат ожидание произведения случайных величин.Содержание книги
Поиск на нашем сайте
M[X]=mx= (M[X], M[Y])-центр распределения. Пусть X и Y - случ. вел. С конечными мат. ожиданиями. Мат. ожидание их суммы равно сумме их мат. ожиданий. M[X+Y]= M[X]+M[Y] Пусть X и Y- взаимно независимые случ. вел с конечными мат. ожиданиями. Мат ожидание произведения XY равно произведению их мат. ожиданий. M[XY]= Пусть X и Y- случ. Вел с совместным распределением, задаваемым таблицей (1). Условное мат. ожидание случ. dел. X при условии, что Y принимает заданное значение Y = yj, вычисляется по формуле: M[X/Y=yj]= Дисперсия суммы случайных величин: D[X+Y] z=X+Y => D[z]=M[(z-mz)2], а mz=mx+my D[z]= M[((X-mx)+(Y-my))2]= M[(X-mx)2]+2 M[(X-mx)(Y-my)]+ M[(Y-my)2]=D[X]+2cov(X,Y)+D[Y] Таким образом: D[X±Y]=D[X]+D[Y]±2cov(X,Y) Если X и Y независимые, то cov(X,Y)=0 => D[X±Y]=D[X]+D[Y] Рассмотрим D[aX±bY]=a2D[X]+b2D[Y]±2abcov(X,Y) Коэффициент корреляции как характеристика статистической связи. Некоррелированность и независимость случ. величин. В качестве меры линейной зависимости между случ. величинами X и Y используют коэффициент корреляции, вычисляемый по формуле
Св-ва коэфиициента корреляции: 1. Док-во: рассмотрим систему 2-ух случ. вел: (X,Y) Проведем нормировку (стандартизацию), т.е. M[X]= mx D[X]=σx2 Xxнормиров= M[Y]=my D[Y]= σy2 Yyнормиров= Cov(Xx,Yy)=M[{ 2. Если X и Y – незав. случ. вел, то 3.Если X и Y связаны линейной функциональной зависимостью: Y=aX+b, где a,b – const, a≠0,то Док-во: Т.к M[Y]=aM[X]+b=amx+b, то имеем cov(X,Y)=M[(X-mx)*(Y-my)]=M[(X-mx)(aX+b-amx-b)]=M[(X-mx)a(X-mx)]=aD[X] Вычислим дисперсию случ. вел. Y=aX+b D[Y]=D[aX+b]=a2D[X] Таким образом, коэффициент корреляции равен:
Т.е коэффициент корреляции является показателем линейной зависимости, но если ρxy=0. это не значит,что между ними нет никакой связи, это значит, что нет линейной зависимости. Если коэффициент корреляции между случ. вел. X и Y равен 0, то говорят, что X и Y некоррелированны. Некоррелированность случ. вел X и Y означает только, что между ними нет линейной зависимости и не означает статистическую независимость случ. вел X и Y. Законы больших чисел и предельные теоремы. Теорема Бернулли, Чебышева, Муавра-Лапласа Теорема Чебышева и ее обобщение.
Если дисперсии n-независимых случайных величин (X1…Xn) ограничены одной и той же постоянной, то при неограниченном увеличении числа n среднее арифметическое случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий.
Док-во: По условию: M(
По первому неравенству Чебышева получаем:
поскольку P>1, то:
Вывод: при достаточно больших n выполнение рассматриваемого неравенства является событием практически достоверным, а неравенства противоположного смысла практически невозможно. Таким образом предел по вероятности следует понимать не как категорическое отверждение, а как утверждение, вероятность которого гарантируется с вероятностью близкой к 1 (при n->∞) Таким образом, при большом числе случайных величин практически достоверно, что их средняя случайная величина как угодна мало отличается от неслучаной – среднего математического ожидания, т.е. перестает быть случайной. Этим заключением обоснован выбор средней арифметической в качестве меры истинного значения мат. ожидания. Теорема Бернулли.
Пусть А – случайный исход некоторого экспериментов, P(A)=p – вероятность этого исхода. Предположим, что эксперимент повторяется n раз в неизменных условиях (т.е. вероятность Р(А)=р не изменяется при повторении экспериментов). Тогда относительная частота появление события А при n -> ∞ сходится по вероятности к р:
где n – общее число исходов, m – число благоприятных исходов, p – вероятность появления случ. величины. Док-во: Пусть Вычислим математическое ожидание случайной величины M[Xi] = 1*p + 0*q = p И математическое ожидание их среднего арифметического:
Случайные величины
Теорема Бернулли дает математическое обоснование экспериментальным результатам, в которых наблюдается устойчивость частот при увеличении числа экспериментов. Устойчивость среднего арифметического можно объяснить тем, что случайное отклонения от среднего, неизбежные в каждом отдельном результате, в массе однородных результатов взаимно поглощаются, нивелируются, выравниваются. Вследствие этого средний результат фактически перестает быть случайным и может быть предсказан достаточно точно. Теорема Муавра-Лапласа. Пусть Х – случайная величина, имеющая биномиальное распределение. (q=1-p; n испытаний) Х – число успехов в n испытаниях по схеме Бернулли Х=0…n
Введем величину Причем
X = X1 + … + Xn (они все независимы и имеют одинаковое распределение) M[X] = M[X1 + … + Xn] = M[X1] + … + M[Xn] = np D[X] = D[X1 + … + Xn] = D[X1] + … + D[Xn] = npq Следовательно: X
Теорема Муавра-Лапласа позволяет количественно оценить разброс события А в некотором эксперименте, который может повторятся n раз в неизменных условиях.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 396; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.103.185 (0.008 с.) |

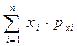 M[Y]=my=
M[Y]=my= 
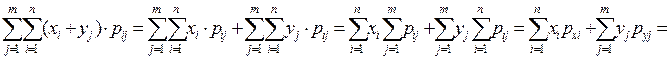
 =M[X]*M[Y]. Это правило распространяется на любое конечное число взаимно независимых случ. величин. Заметим, то последнее равенство для зависимых случ. величин, вообще говоря, е выполняется.
=M[X]*M[Y]. Это правило распространяется на любое конечное число взаимно независимых случ. величин. Заметим, то последнее равенство для зависимых случ. величин, вообще говоря, е выполняется.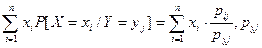 >0
>0

 Нормированная величина – это тогда, когда
Нормированная величина – это тогда, когда mч=0, а σx=1
mч=0, а σx=1 }]*M[{
}]*M[{  }]=
}]= 
 , причем обратное неверно
, причем обратное неверно
 Следовательно,
Следовательно,  =1, если a>1 и
=1, если a>1 и =-1, если a<0
=-1, если a<0

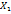 )=
)=  … M(
… M( )=
)= 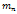



 , или
, или 
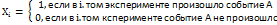 Причем
Причем  , а
, а  .
. :
:

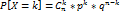

 M[Xi]=1*p+0*q=p
M[Xi]=1*p+0*q=p




