Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства дисперсии случайной величины.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дисперсией (рассеянием) дискретной случайной величины D(X) называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания 1 свойство. Дисперсия постоянной величины C равна нулю; D(C) = 0. Доказательство. По определению дисперсии, D(C) = M{[C – M(C)]2}. Из первого свойства математического ожидания D(C) = M[(C – C)2] = M(0) = 0. 2 свойство. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(CX) = C2 D(X) Доказательство. По определению дисперсии, D(CX) = M{[CX – M(CX)]2} Из второго свойства математического ожидания D(CX)=M{[CX – CM(X)]2}= C2M{[X – M(X)]2}=C2D(X) 3 свойство. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D[X + Y ] = D[X] + D[Y ]. Доказательство. По формуле для вычисления дисперсии имеем D(X + Y) = M[(X + Y)2] − [M(X + Y)]2 Раскрыв скобки и пользуясь свойствами математического ожидания суммы нескольких величин и произведения двух независимых случайных величин, получим D(X + Y) = M[X2+ 2XY + Y2] − [M(X) + M(Y)]2 = M(X2) + 2M(X)M(Y) + M(Y2) − M2(X) − 2M(X)M(Y) − M2(Y) = {M(X2) − [M(X)]2}+{M(Y2) − [M(Y)]2} = D(X) + D(Y). Итак, D(X + Y) = D(X) + D(Y) 4 свойство. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D(X − Y) = D(X) + D(Y) Доказательство. В силу третьего свойства D(X − Y) = D(X) + D(–Y). По второму свойству D(X − Y) = D(X) + (–1)2 D(Y) или D(X − Y) = D(X) + D(Y) Числовые характеристики систем случайных величин. Коэффициент корреляции, свойства коэффициента корреляции. Корреляционный момент. Характеристикой зависимости между случайными величинами
Для вычисления корреляционного момента дискретных величин используют формулу:
а для непрерывных величин – формулу:
Коэффициентом корреляции rxy случайных величин X и Y называют отношение корреляционного момента к произведению среднеквадратичных отклонений величин: Свойства коэффициента корреляции: 1. Если Х и У независимые случайные величины, то r =0; 2. -1≤ r ≤1.При этом, если |r| =1, то между Х и У функциональная, а именно линейная зависимость; 3. r характеризует относительную величину отклонения М(ХУ) от М(Х)М(У), и т.к. отклонение имеет место только для зависимых величин, то rхарактеризует тесноту зависимости. Линейная функция регрессии. Рассмотрим двумерную случайную величину (X, Y), где X и У — зависимые случайные величины. Представим одну из величин как функцию другой. Ограничимся приближенным представлением (точное приближение, вообще говоря, невозможно) величины Y в виде линейной функции величины X:
Теорема. Линейная средняя квадратическая регрессия Y на X имеет вид
Коэффициент β=rσy/σx называют коэффициентом регрессии Y на X, а прямую
Неравенство Маркова. Формулировка неравенства Маркова Если среди значений случайной величины Х нет отрицательных, то вероятность того, что она примет какое-нибудь значение, превосходящее положительное число А, не больше дроби а вероятность того, что она примет какое-нибудь значение, не превосходящее положительного числа А, не меньше Неравенство Чебышева. Неравенство Чебышева. Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа ε, не меньше, чем 1 −D[X]ε2 P(|X – M(X)| < ε) ≥ 1 –D(X)ε2 Доказательство. Так как события, состоящие в осуществлении неравенств P(|X−M(X)| < ε) и P(|X – M(X)| ≥ε) противоположны, то сумма их вероятностей равна единице, т. е. P(|X – M(X)| < ε) + P(|X – M(X)| ≥ ε) = 1. Отсюда интересующая нас вероятность P(|X – M(X)| < ε) = 1 − P(|X – M(X)| > ε). Таким образом, задача сводится к вычислению вероятности P(|X –M(X)| ≥ ε). Напишем выражение для дисперсии случайной величины X D(X) = [x1 – M(x)]2p1 + [x2 – M(x)]2p2 +... + [xn – M(x)]2pn Все слагаемые этой суммы неотрицательны. Отбросим те слагаемые, у которых |xi – M(X)| < ε (для оставшихся слагаемых |xj – M(X)| ≥ ε), вследствие чего сумма может только уменьшиться. Условимся считать для определенности, что отброшено k первых слагаемых (не нарушая общности, можно считать, что в таблице распределения возможные значения занумерованы именно в таком порядке). Таким образом, D(X) ≥ [xk+1 – M(x)]2pk+1 + [xk+2 – M(x)]2pk+2 +... + [xn – M(x)]2pn Обе части неравенства |xj –M(X)| ≥ ε (j = k+1, k+2,..., n) положительны, поэтому, возведя их в квадрат, получим равносильное неравенство |xj – M(X)|2 ≥ε2.Заменяя в оставшейся сумме каждый из множителей |xj – M(X)|2числом ε2(при этом неравенство может лишь усилиться), получим D(X) ≥ ε2(pk+1 + pk+2 +... + pn) По теореме сложения, сумма вероятностей pk+1+pk+2+...+pn есть вероятность того, что X примет одно, безразлично какое, из значений xk+1 +xk+2 +...+xn, а при любом из них отклонение удовлетворяет неравенству |xj – M(X)| ≥ ε. Отсюда следует, что сумма pk+1 + pk+2 +... + pn выражает вероятность P(|X – M(X)| ≥ ε). Это позволяет переписать неравенство для D(X) так D(X) ≥ ε2P(|X – M(X)| ≥ ε) или P(|X – M(X)|≥ ε) ≤D(X)/ε2 Окончательно получим P(|X – M(X)| < ε) ≥D(X)/ε2
Теорема Чебышева. Теорема Чебышева. Если
будет как угодно близка к единице, если число случайных величин достаточно велико. Другими словами, в условиях теоремы
Доказательство. Введем в рассмотрение новую случайную величину — среднее арифметическое случайных величин
Найдем математическое ожидание Х. Пользуясь свойствами математического ожидания (постоянный множитель можно вынести за знак математического ожидания, математическое ожидание суммы равно сумме математических ожиданий слагаемых), получим
Применяя к величине Х неравенство Чебышева, имеем
или, учитывая соотношение (1)
Пользуясь свойствами дисперсии (постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат; дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых), получим
По условию дисперсии всех случайных величин ограничены постоянным числом С, т.е. имеют место неравенства:
поэтому
Итак,
Подставляя правую часть (2) в неравенство (1) (отчего последнее может быть лишь усилено), имеем
Отсюда, переходя к пределу при n→∞, получим
Наконец, учитывая, что вероятность не может превышать единицу, окончательно можем написать
Теорема доказана. Теорема Бернулли. Теорема Бернулли. Если в каждом из n независимых испытаний вероятность p появления события A постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико. Другими словами, если ε — сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство
Доказательство. Обозначим через X1 дискретную случайную величину — число появлений события в первом испытании, через X2 — во втором,..., Xn — в n -м испытании. Ясно, что каждая из величин может принять лишь два значения: 1 (событие A наступило) с вероятностью p и 0 (событие не появилось) с вероятностью Можно ли применить к рассматриваемым величинам теорему Чебышева? Можно, если случайные величины попарно независимы и дисперсии их ограничены. Оба условия выполняются Действительно, попарная независимость величин Применяя теорему Чебышева (частный случай) к рассматриваемым величинам, имеем
Приняв во внимание, что математическое ожидание a каждой из величин
Остается показать, что дробь
Учитывая это равенство, окончательно получим
|
||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 7947; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.78.184 (0.008 с.) |

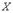 и
и  служит математическое ожидание произведения отклонений
служит математическое ожидание произведения отклонений  от их центров распределений (так иногда называют математическое ожидание случайной величины), которое называется корреляционным моментом или ковариацией:
от их центров распределений (так иногда называют математическое ожидание случайной величины), которое называется корреляционным моментом или ковариацией: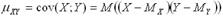


 - коэффициент корреляции;
- коэффициент корреляции;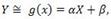 где α и β — параметры, подлежащие определению.
где α и β — параметры, подлежащие определению.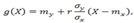 где mx=M(X), my=M(Y), σx=√D(X), σy=√D(Y), r=µxy/(σxσy)— коэффициент корреляции величин X и Y.
где mx=M(X), my=M(Y), σx=√D(X), σy=√D(Y), r=µxy/(σxσy)— коэффициент корреляции величин X и Y.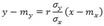 называют прямой среднеквадратической регрессии Y на X.
называют прямой среднеквадратической регрессии Y на X.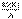 , т.е.
, т.е. ,
, , т.е.
, т.е.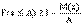 .
.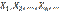 — попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С ), то, как бы мало ни было положительное число ε, вероятность неравенства
— попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С ), то, как бы мало ни было положительное число ε, вероятность неравенства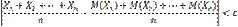
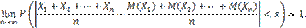
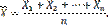
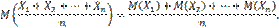 (1)
(1)
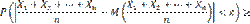
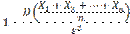
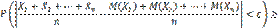
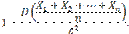
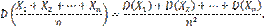
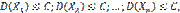
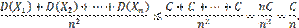
 (2)
(2)
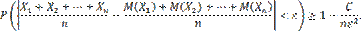
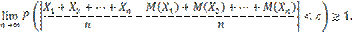
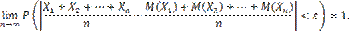
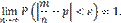
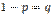 .
.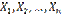 следует из того, что испытания независимы. Дисперсия любой величины
следует из того, что испытания независимы. Дисперсия любой величины  равна произведению
равна произведению 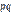 ; так как
; так как 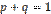 , то произведение
, то произведение 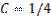 .
.
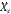 (т.е. математическое ожидание числа появлений события в одном испытании) равно вероятности p наступления события, получим
(т.е. математическое ожидание числа появлений события в одном испытании) равно вероятности p наступления события, получим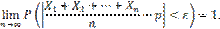
 равна относительной частоте
равна относительной частоте 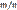 появлений события A в испытаниях. Действительно, каждая из величин
появлений события A в испытаниях. Действительно, каждая из величин 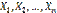 при появлении события в соответствующем испытании принимает значение, равное единице; следовательно, сумма
при появлении события в соответствующем испытании принимает значение, равное единице; следовательно, сумма 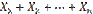 равна числу
равна числу  появлений события в
появлений события в 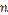 испытаниях, а значит,
испытаниях, а значит,