Локальная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа.

Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р_n (k) того, что событие А появится в п испытаниях ровно k раз, приближенно равна (тем точнее, чем больше п) значению функции

, где

Интегральная теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(k₁, k₂) того, что событие А появится в п испытаниях от k₁ до k₂ раз, приближенно равна определенному интегралу:

- интегральная функция Лапласа.

Дискретная случайная величина: определение, закон распределения, функция распределения. Числовые характеристики дискретной случайной величины.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретной (прерывной)называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая — их вероятности:

 

сумма вероятностей второй строки таблицы, равна единице: p ₁ +p ₂ + …+p_n= 1.

многоугольником распределения

Функцией распределения случайной величины X называется функция F(x), выражающая для каждого x вероятность того, что случайная величина X примет значение, меньшее x.

F(x) = P(X < x). Функция F(x) называется также интегральной функцией распределения или интегральным законом распределения.

Геометрически функция распределения интерпретируется как вероятность того, что случайная точка X попадет левее заданной точки x.

Числовые характеристики:

Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее возможных значений на соответствующие вероятности :

Математическое ожидание называют также средним значением случайной величины Х

Дисперсией D(X) случайной величины Х называют средний квадрат отклонения случайной величины от ее центра распределения:

.

Для того, чтобы рассматривать отклонение в тех же единицах, что и значения случайной величины, вводится еще одна характеристика – среднее квадратическое отклонение s(Х), которое определяется как

.

 

Биноминальное распределение.

Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, вероятность непоявления q =1— р). Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях.

Биномиальное распределение — дискретное распределение вероятностей случайной величины ξ, принимающей целочисленные значения с вероятностями

где — параметр биномиального распределения, иногда называемый «вероятностью положительного исхода»; одно из основных распределений вероятностей, порождаемых конечным множеством независимых случайных экспериментов (испытаний).

 

Распределение Пауссона.

Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Если вероятность события мала (р 0, 1). В этих случаях (n велико, р мало) прибегают к асимптотической формуле Пуассона.

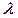Произведение nр сохраняет постоянное значение, а именно nр = . Это означает, что среднее число появлений события в различных сериях испытаний, т. е. при различных значениях n, остается неизменным.

Таким образом,
P_n (k) = Эта формула выражает закон распределения Пуассона вероятностей массовых (n велико) и редких (р мало) событий.