
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двумерная дискретная случайная величина: закон совместного распределения, частные законы распределения компонент. Условные законы распределения компонент. Независимость случайных величин.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Закон распределения дискретной двумерной случайной величины (Х, Y) имеет вид таблицы с двойным входом, задающей перечень возможных значений каждой компоненты и вероятности p (xi, yj), с которыми величина принимает значение (xi, yj):
При этом сумма вероятностей, стоящих во всех клетках таблицы, равна 1. Зная закон распределения двумерной случайной величины, можно найти законы распределения ее составляющих. Действительно, событие Х = х 1 представляется собой сумму несовместных событий (X = x 1, Y = y 1), (X = x 1, Y = y 2),…, (X = x 1, Y = ym), поэтому р (Х = х 1) = p (x 1, y 1) + p (x 1, y 2) +…+ p (x 1, ym) (в правой части находится сумма вероятностей, стоящих в столбце, соответствующем Х = х 1). Так же можно найти вероятности остальных возможных значений Х. Для определения вероятностей возможных значений Y нужно сложить вероятности, стоящие в строке таблицы, соответствующей Y = yj. Условные законы распределения составляющих дискретной двумерной случайной величины. Рассмотрим дискретную двумерную случайную величину и найдем закон распределения составляющей Х при условии, что Y примет определенное значение (например, Y = у 1). Для этого воспользуемся формулой Байеса, считая гипотезами события Х = х 1, Х = х 2,…, Х = хп, а событием А – событие Y = у 1. При такой постановке задачи нам требуется найти условные вероятности гипотез при условии, что А произошло. Следовательно,
Таким же образом можно найти вероятности возможных значений Х при условии, что Y принимает любое другое свое возможное значение:
Аналогично находят условные законы распределения составляющей Y:
Случайные величины называются независимыми, если закон распределения одной из них не зависит от того какое значение принимает другая случайная величина. Теорема. Для того, чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы функция распределения системы (X, Y) была равна произведению функций распределения составляющих.
Свойства математического ожидания случайной величины 1 свойство. Математическое ожидание постоянной величины равно самой постоянной: M(C) = C. Доказательство. Будем рассматривать постоянную C как дискретную случайную величину, которая имеет одно возможное значение C и принимает его с вероятностью p = 1. Следовательно, M(C) = C · 1 = C.
2 свойство. Постоянный множитель можно выносить за знак математического ожидания: M(CX) = CM(X). Доказательство. Пусть случайная величина X задана законом распределения вероятностей: X x1 x2... xn p p1 p2... pn Напишем закон распределения случайной величины CX: CX Cx1 Cx2... Cxn p p1 p2... pn Математическое ожидание случайной величины CX: M(CX) = Cx1p1 + Cx2p2 +... + Cxnpn = C(x1p1 + x2p2 +... + xnpn) = CM(X) Итак, М(СХ) = СМ(Х) 3 свойство. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M(XY) = M(X)M(Y). Доказательство. Пусть независимые случайные величины X и Y заданы своими законами распределения. X x1 x2 ; Y y1 y2 p g1 g2 p p1 p2 Составим все значения, которые может принимать случайная величина XY. Для этого перемножим все возможные значения X на каждое возможное значение Y. Напишем закон распределения: XY x1y1 x2y1 x1y2 x2y2 p p1g1 p2g1 p1g2 p2g2 Математическое ожидание равно сумме произведений всех возможных значений на их вероятности: M(XY) = x1y1 · p1g1 + x2y1 · p2g1 + x1y2 · p1g2 + x2y2 · p2g2. или M(XY) = y1g1(x1p1 + x2p2) + y2g2(x1p1 + x2p2) = (x1p1 + x2p2)(y1g1 + y2g2) = M(X)M(Y). 4 свойство. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: M[X + Y ] = M[X] + M[Y ] Доказательство. Пусть случайные величины X и Y заданы следующими законами распределения X x1 x2 Y y1 y2 p g1 g2 p p1 p2 Составим все возможные значения величины X + Y. Для этого к каждому возможному значению X прибавим каждое возможное значение Y; получим x1 + y1, x1 + y2, x2 + y1, x2 + y2, и обозначим их вероятности соответственно через p11, p12, p21, p22. Математическое ожидание величины X + Y равно M(X + Y) = (x1 + y1)p11 + (x1 + y2)p12+(x2 + y1)p21 + (x2 + y2)p22. Докажем, что p11 + p12 = p1. Событие, состоящее в том, что X примет значение x1, (вероятность этого события равна p1) влечет за собой событие, которое состоит в том, что X + Y примет значение x1 + y1 или x1 + y2. Отсюда и следует, p11 + p12 = p1 Подставляя правые части этих равенств в соотношение для M(X + Y), получим M(X + Y) = (x1p1 + x2p2) + (y1g1 + y2g2) = M(X) + M(Y).
|
|||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.236.174 (0.011 с.) |

 .
.
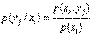 .
.


