
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсия и ее свойства. Среднее квадратическое отклонение.Содержание книги
Поиск на нашем сайте
Во многих практически важных случаях существенным является вопрос о том, насколько велики отклонения
Пусть
с теми же вероятностями p1, p2,..., pn. Следовательно, согласно определению математического ожидания дискретной случайной величины, имеем
Если же
Принимая во внимание определение дисперсии и свойства математического ожидания, имеем
Так как
Следовательно,
Откуда окончательно находим
1°. Дисперсия постоянной равна нулю. (Доказательство) 2°. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
(Доказательство)
3°. Если
(Доказательство)
Средним квадратическим отклонением
Пример 1. Cлучайная величина Решение: Используя формулы (39), (44) и (49) соответственно получим
Пример 2. Cлучайная величина Решение: Величина
Решение: Пусть
Пример 4. Пусть
[См. формулу (17)]. Найти: Решение: Используя соотношение (39), получим
Пример 5. Пусть
[См. формулу (27)]. Найти математическое ожидание, дисперсию и средне квадратическое отклонение cлучайной величины. Решение: По формулам (40), (45) и (49) находим
,то по формуле (40) находим
Проведем в интеграле замену переменной, полагая
тогда
Следовательно,
Но
[См. формулу (29)]. Далее, так как функция
Следовательно, Дисперсию находим по формуле (45)
(вычисление интеграла не приводим). Итак,
Таким образом, параметры a и
* Казалось бы естественным рассматривать не квадрат отклонения, а просто отклонение
Здесь мы воспользовались тем, что
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.99.18 (0.008 с.) |

 случайной величины от ее математического ожидания.
случайной величины от ее математического ожидания.  и
и  заданы следующими рядами распределения
заданы следующими рядами распределения
 случайной величины
случайной величины 
 принимает значения
принимает значения

 , то по определению
, то по определению

 и
и 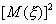 - постоянные, то используя свойства математического ожидания, получим
- постоянные, то используя свойства математического ожидания, получим




 случайной величины
случайной величины 




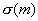
 - случайная величина, принимающая значения 1 или 0 в зависимости от того, происходит или не происходит событие A в i -м опыте. Тогда
- случайная величина, принимающая значения 1 или 0 в зависимости от того, происходит или не происходит событие A в i -м опыте. Тогда  . Ясно, что
. Ясно, что  ,
,  для любого i. На основании свойства 3° для математического ожидания и дисперсии имеем
для любого i. На основании свойства 3° для математического ожидания и дисперсии имеем 






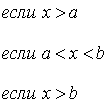
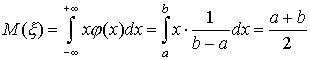


 (см. § 3, п.5). Найдем
(см. § 3, п.5). Найдем 





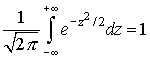
 нечетная, то по свойству нечетных функций
нечетная, то по свойству нечетных функций




 . Однако, как правило, действия связанные с абсолютными величинами, приводят к громоздким вычислениям.
. Однако, как правило, действия связанные с абсолютными величинами, приводят к громоздким вычислениям.


