Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условная вероятность. Теорема умножения вероятностей.Содержание книги
Поиск на нашем сайте Во многих задачах приходится находить вероятность совмещения событий А и В, если известны вероятности событий А и В. Рассмотрим следующий пример. Пусть брошены две монеты. Найдем вероятность появления двух гербов. Мы имеем 4 равновероятных попарно несовместных исхода, образующих полную группу:
Пусть теперь нам стало известно, что на первой монете выпал герб. Как изменится после этого вероятность того, что герб появится на обеих монетах? Так как на первой монете выпал герб, то теперь полная группа состоит из двух равновероятных несовместных исходов:
Новую вероятность события А, в предположении, что произошло событие B, будем обозначать PB(А). Таким образом, Р(A)=1/4; PB(А)=1/2 Теорема умножения. Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.
Доказательство. Докажем справедливость соотношения (4), опираясь на классическое определение вероятности. Пусть возможные исходы Е1, Е2,..., ЕN данного опыта образуют полную группу равновероятных попарно несовместных событий, из которых событию A благоприятствуют M исходов, и пусть из этих M исходов L исходов благоприятствуют событию B. Очевидно, что совмещению событий A и B благоприятствуют L из N возможных результатов испытания. Это дает
Из соотношения (6) вытекает, что из двух равенств (8) одно является следствием другого. Пусть, например, событие A — появление герба при однократном брссании монеты, а событие B — появление карты бубновой масти при вынимании карты из колоды. Очевидно, что события A и B независимы. В случае независимости событий A к B формула (4) примет более простой вид:
т. е. вероятность совмещения двух независимых событий равна произведению вероятностей этих событий. События А1, А2,..., Аn называются независимыми в совокупности, если вероятность наступления каждого из них не меняет своего значения после того, как одно или несколько из остальных событий осуществились. Исходя из этого определения, в случае независимости событий А1, А2,..., Аn между собой в совокупности на основании формулы (7) имеем
Пример 1. Какова вероятность того, что при десятикратном бросании монеты герб выпадет 10 раз? Решение: Пусть событие Ai — появление герба при i -м бросании. Искомая вероятность есть вероятность совмещения всех событий Ai (i=1,2,3,...,10), а так как они, очевидно, независимы в совокупности, то применяя формулу (10), имеем
Пример 2. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течение часа станок не потребует внимания рабочего, для первого станка равна 0,9, для второго — 0,8, для третьего — 0,7. Найти: 1) вероятность р того, что в течение часа ни один из трех станков не потребует внимания рабочего; 2) вероятность того, что в течение часа по крайней мере один из станков не потребует внимания рабочего. Решение:
2) Вероятность того, что в течение часа станок потребует внимания рабочего для первого станка равна 1—0,9=0,1, для второго и для третьего станков она соответственно равна 1—0,8=0,2 и 1—0,7=0,3. Тогда вероятность того, что в течение часа все три станка потребуют внимания рабочего, на основании формулы (10) составляет
Событие A, заключающееся в том, что в течение часа все три станка потребуют внимания рабочего, противоположно событию
Пример 3. Из урны, содержащей 3 белых и 7 черных шаров, вынимают два шара. Какова вероятность того, что оба шара окажутся белыми? Решение: Эта задача уже была решена в п. 3 с помощью классического определения вероятности. Решим ее, применяя формулу (5). Извлечение двух шаров равносильно последовательному их извлечению. Обозначим через А появление белого шара при первом извлечении, а через В — при втором. Событие, состоящее в появлении двух белых шаров, является совмещением событий А и В. По формуле (5) имеем
Но Р(А)=3/10; РA(В)=2/9, поскольку после того, как был вынут первый белый шар, в урне осталось 9 шаров, из которых 2 белых. Следовательно,
Формула полной вероятности. Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2,..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A,..., HnA. Следовательно,
Применяя аксиому сложения вероятностей, имеем
Но
Эта формула называется формулой полной вероятности. События H1, H2,..., Hn часто называют «гипотезами».
Пример. В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах: с 1-го завода 250 шт., со 2-го — 525 шт., с 3-го — 275 шт. и с 4-го — 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0,15, для 2-го — 0,30, для 3-го — 0,20, для 4-го — 0,10. При раскладке по полкам магазина лампочки были перемешаны. Какова вероятность того, что купленная лампочка прогорит более 1500 часов? Решение: Пусть A — событие, состоящее в том, что лампочка прогорит более 1500 часов, а Н1, Н2, Н3 и Н4 — гипотезы, что она изготовлена соответственно 1, 2, 3 или 4-м заводом. Так как всего лампочек 2000 шт., то вероятности гипотез соответственно равны
Далее, из условия задачи следует, что
Используя формулу полной вероятности (11), имеем
Формула Бейеса. Предположим, что производится некоторый опыт, причем об условиях его проведения можно высказать n единственно возможных и несовместных гипотез Спрашивается, как изменятся вероятности гипотез, если стало известным, что событие А произошло? Иными словами, нас интересуют значения вероятностей На основании соотношений (4) и (5) имеем
откуда
Но по формуле полной вероятности
Поэтому
Формула (12) называется формулой Бейеса*.
Пример. На склад поступило 1000 подшипников. Из них 200 изготовлены на 1-м заводе, 460—на 2-м и 340 - на 3-м. Вероятность того, что подшипник окажется нестандартным, для 1-го завода равна 0,03, для 2-го — 0,02, для 3-го — 0,01. Взятый наудачу подшипник оказался н естандартным. Какова вероятность того, что он изготовлен 1-м заводом? Решение: Пусть A — событие, состоящее в том, что взятый Подшипник нестандартный, а
Найдем
Таким образом, вероятность гипотезы, что подшипник изготовлен 1-м заводом, изменилась после того, как стало известно, что он нестандартен.
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 472; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

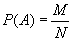 ;
;  ;
; 





 и
и 
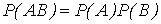




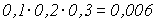
 , состоящему в том, что по крайней мере один из станков не потребует внимания рабочего. Поэтому по формуле (3) получаем
, состоящему в том, что по крайней мере один из станков не потребует внимания рабочего. Поэтому по формуле (3) получаем 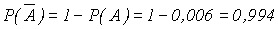
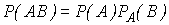



 (i=1, 2,..., n), поэтому
(i=1, 2,..., n), поэтому



 , имеющих вероятности
, имеющих вероятности 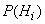 . Пусть в результате опыта может произойти или не произойти событие А, причем известно, что если опыт происходит при выполнении гипотезы
. Пусть в результате опыта может произойти или не произойти событие А, причем известно, что если опыт происходит при выполнении гипотезы  , то
, то 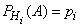

 .
.



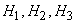 - гипотезы, что он изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных гипотез составляют
- гипотезы, что он изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных гипотез составляют

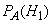 , т. е. вероятность того, что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле Бейеса имеем
, т. е. вероятность того, что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле Бейеса имеем