Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последовательные испытания. Формула Бернулли.
Предположим, что производится n независимых испытаний, в результате каждого из которых может наступить или не наступить некоторое событие A. Пусть при каждом испытании вероятность наступления события А равна P(A)=p и, следовательно, вероятность противоположного события (ненаступления А) равна Всякую комбинацию, в которую А входит m раз и
Так как в любой другой благоприятной комбинации Вi событие A встречается также m раз, а событие
Формула (13) называется формулой Бернулли *. Пример 1. Вероятность попадания в цель при одном выстреле равна 0,6. Какова вероятность того, что 8 выстрелов дадут 5 попаданий? Решение: Здесь Используя формулу (13'), имеем
Часто необходимо знать, при каком значении m вероятность принимает наибольшее значение, т. е. требуется найти наивероятнейшее число
Пример 2. Определить наивероятнейшее число попаданий в цель в примере 1. Решение: Здесь Согласно формуле (14) наивероятнейшее значение
Формула (15) выражает так называемую локальную теорему Лапласа **. Точность этой формулы повышается с возрастанием n. Функция
Таблица I.
Пример 3. Игральную кость бросают 80 раз. Определить вероятность того, что цифра 3 появится 20 раз. Решение: Здесь далее находим
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Понятие случайной величины является основным в теории вероятностей и ее приложениях. Случайными величинами, например, являются число выпавших очков при однократном бросании игральной кости, число распавшихся атомов радия за данный промежуток времени, число вызовов на телефонной станции за некоторый промежуток времени, отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе и т. д.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.190.93 (0.01 с.) |
 . Определим вероятность Pn(m) того, что событие А произойдет m раз при n испытаниях. При этом заметим, что наступления или ненаступления события А могут чередоваться различным образом. Условимся записывать возможные результаты испытаний в виде комбинаций букв А и
. Определим вероятность Pn(m) того, что событие А произойдет m раз при n испытаниях. При этом заметим, что наступления или ненаступления события А могут чередоваться различным образом. Условимся записывать возможные результаты испытаний в виде комбинаций букв А и  . Например, запись
. Например, запись  означает, что в четырех испытаниях событие осуществилось в 1-м и 4-м случаях и не осуществилось во 2-м и 3-м случаях.
означает, что в четырех испытаниях событие осуществилось в 1-м и 4-м случаях и не осуществилось во 2-м и 3-м случаях.

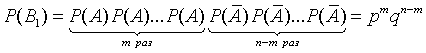
 . Итак
. Итак
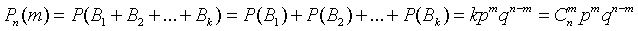




 наступления события A в данной серии опытов. Можно доказать, что число
наступления события A в данной серии опытов. Можно доказать, что число 
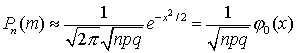

 , как мы увидим в дальнейшем, играет очень большую роль в теории вероятностей. Ее значения при различных значениях аргумента приведены в Приложении (см. табл. I).
, как мы увидим в дальнейшем, играет очень большую роль в теории вероятностей. Ее значения при различных значениях аргумента приведены в Приложении (см. табл. I).