
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывные случайные величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Непрерывная случайная величина X принимает значения из некоторого конечного или бесконечного промежутка. Она может быть задана функцией распределения вероятностей (интегральной функцией) или плотностью распределения вероятностей (дифференциальной функцией). Функцией распределения вероятностей случайной величины Х называют функцию F(x), определяющую для каждого значения Х вероятность того, что случайная величина Х примет значение, меньше х, т.е. 1) 2) 3) Плотностью распределения вероятностей называют первую производную от функции распределения: 1) 2) 3) 4) Математическое ожидание непрерывной случайной величины Х определяется по формуле:
Дисперсия непрерывной случайной величины Х, определяется по формуле:
Если Среднее квадратическое отклонение определяется как корень квадратный из дисперсии:
1 Даны законы распределения дискретной случайной величины: а)
б)
Найти функцию распределения случайной величины Х и построить ее график. 2 По данным задачи 5, темы 4 составить функцию распределения случайной величины Х и построить ее график. 3 По данным задачи 6, темы 4 составить функцию распределения случайной величины Х и начертить ее график 4 По одному варианту задачи 14, темы 4 составить функцию распределения случайной величины Х и начертить ее график. 5 Найти функцию распределения случайной величины Х – числа попаданий в цель, если произведено три выстрела с вероятностью попадания в цель при каждом выстреле 0,8. 6 Вероятность сдачи первого экзамена студентом составляет 0,7, второго 0,6 и третьего 0,8. Найти функцию распределения случайной величины Х-числа экзаменов, сданных студентом. Определить М(Х). 7 Случайная величина Х задана функцией распределения: а) Найти вероятность того, что в результате испытания случайная величина Х примет значение: а) меньше 0; б) меньше 1; в) не меньше 1; г) заключенное в интервале (0;2). 8 Дана функция распределения случайной величины Х: а) Найти вероятность того, что в результате шести испытаний случайная величина Х два раза примет значение, принадлежащее интервалу (0;1). 9 Случайная величина задана функцией: а) Найти: а) плотность распределения вероятностей (дифференциальную функцию) случайной величины Х; б) математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины Х. 10 Дана функция распределения случайной величины Х:
а) Определить вероятность попадания случайной величины в интервал (-а;а). б) Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 11 Случайная величина Х задана функцией: а)
Найти значения А и В, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 12 Случайная величина Х задана функцией:
Найти: а) плотность распределения случайной величины Х; б) вероятность того, что в результате четырех независимых испытаний случайная величина Х хотя бы один раз примет значение, принадлежащее интервалу 13 Случайная величина Х задана функцией:
Найти: а) плотность распределения случайной величины Х; б) вероятность попадания случайной величины в интервал (2,5; 3); в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х; г) моду и медиану величины Х. Построить графики функций. 14 Случайная величина Х задана плотностью распределения:
Найти: а) функцию распределения F(x); б) вероятность попадания случайной величины в интервал 15 Случайная величина Х задана плотностью распределения:
Определить: а) функцию распределения случайной величины Х; б) вероятность попадания случайной величины в интервал (1;1,2). Начертить графики функций F(x) и f(x). 16 Случайная величина Х задана плотностью распределения:
Определить: а) функцию распределения случайной величины Х; б) вероятность попадания случайной величины в интервал (ln2; 1,2ln 2). Начертить графики функций F(x) и f(x). 17 Случайная величина Х задана плотностью распределения:
Найти: а) функцию распределения случайной величины Х; б) вероятность того, что в результате испытания случайная величина Х примет значение, заключенное в интервале 18 Случайная величина Х задана плотностью распределения:
Найти: а) функцию распределения случайной величины Х и начертить её график; б) вероятность попадания случайной величины Х в интервал 19 Случайная величина Х задана функцией:
Определить: а) значение а; б) математическое ожидание; в) вероятность попадания случайной величины в интервал (1;2). Построить графики функций F(x) и f(x). 20 Дана функция распределения:
Построить графики функций F(x) и f(x). Найти математическое ожидание и дисперсию случайной величины Х. 21 Случайная величина задана плотностью распределения:
Найти: а) постоянную с; б) математическое ожидание, дисперсию и среднее квадратическое отклонение. 22 Случайная величина Х задана дифференциальной функцией 23 Случайная величина Х задана функцией распределения
Найти интегральную функцию распределения случайной величины Х, математическое ожидание, дисперсию и вероятность попадания случайной величины в интервал (-1;3).
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 941; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.006 с.) |

 . Функция распределения имеет следующие свойства:
. Функция распределения имеет следующие свойства: ;
; ;
; . (5.1)
. (5.1)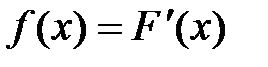 . Функция плотности вероятностей имеет следующие свойства:
. Функция плотности вероятностей имеет следующие свойства: ;
;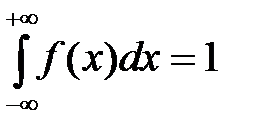 ;
;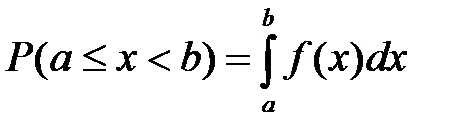 ; (5.2)
; (5.2) . (5.3)
. (5.3) . Если
. Если 
 . (5.4)
. (5.4) , или
, или  . (5.5)
. (5.5) . (5.6)
. (5.6) (5.7)
(5.7) б)
б) 
 б)
б) 
 б)
б) 

 б)
б) 

 ; в) начертить графики функций.
; в) начертить графики функций.





 ; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х.
; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х.
 ; в) математическое ожидание, дисперсию и среднее квадратическое отклонение.
; в) математическое ожидание, дисперсию и среднее квадратическое отклонение.


 при
при 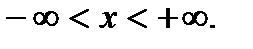 Найти постоянную с.
Найти постоянную с.



