
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретные случайные величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем до опыта заранее неизвестно, какое именно значение она примет. Случайные величины подразделяются на одномерные и многомерные. Различают дискретные и непрерывные случайные величины. Дискретная случайная величина принимает отдельные, изолированные значения, а непрерывная величина принимает все значения на заданном промежутке. Законом или таблицей распределения дискретной случайной величины называют упорядоченный перечень ее возможных значений и соответствующих им вероятностей.
На графике в прямоугольной системе координат наносят точки (хi; pi), которые соединяют отрезками прямых. Полученную ломанную линию называют многоугольником распределения. Математическим ожиданием М(Х) дискретной случайной величины Х называют сумму произведений всех возможных значений случайной величины Х на их вероятности:
Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания служат дисперсия и среднее квадратическое отклонение. Дисперсией D(Х) дискретной случайной величины Х называют математическое ожидание квадрата отклонений случайной величины Х от ее математического ожидания:
где Средним квадратическим отклонением случайной величины Х называют корень квадратный из дисперсии: Биномиальным называют закон распределения дискретной случайной величины Х - числа появления события А в n независимых испытаниях k раз (k = 0,1,2,…, n), если вероятность появления события в k-ом испытании равна р, а вероятность возможного значения Х = k (числа появления события) вычисляют по формуле Бернулли:
Если число испытаний велико, а вероятность появления события в каждом испытании очень мала, то применяют формулу Пуассона:
1 Вероятность работы каждого из четырех комбайнов без поломок в течение определенного времени равна 0,9. Составить закон распределения случайной величины Х – числа комбайнов, работавших безотказно. Построить график распределения вероятностей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 2 Вероятность рождения мальчика 0,515. Составить закон распределения случайной величины Х – числа мальчиков в семьях, имеющих четырех детей. Построить график распределения вероятностей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение. 3 Вероятность того, что покупатель совершит покупку в магазине 0,4. Составить закон распределения случайной величины Х – числа покупателей, совершивших покупку, если магазин посетило 3 покупателя. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. Построить график распределения вероятностей. 4 В группе из 10 спортсменов 6 мастеров спорта. Отбирают (по схеме без возвращения) 3 спортсмена. Составить закон распределения случайной величины Х – числа мастеров спорта из отобранных спортсменов. Найти математическое ожидание случайной величины Х. 5 В группе, состоящей из (2N + 1) студентов, N девушек. Составить закон распределения случайной величины Х – числа девушек из случайно отобранных трех студентов (N – номер студента в группе). 6 В партии из (N+5) изделий (N+1) изделие высокого качества. Случайно отбирается 3 изделия. Составить закон распределения случайной величины Х – числа изделий высокого качества среди отобранных. 7 Стрелок производит выстрелы по цели до первого попадания. Составить закон распределения случайной величины Х – числа выстрелов, сделанных стрелком. Вероятность попадания в цель при каждом выстреле составляет 0,7. Найти наивероятнейшее число выданных стрелку патронов. 8 Покупатель посещает магазины до момента приобретения нужного товара. Вероятность того, что товар имеется в определенном магазине, составляет 0,4. Составить закон распределения случайной величины Х – числа магазинов, которые посетит покупатель из пяти возможных. Построить график распределения. Найти наиболее вероятное число магазинов, которые посетит покупатель. 9 Игрок поочередно покупает билеты двух разных лотерей до первого выигрыша. Вероятность выигрыша по одному билету первой лотереи составляет 0,2, а второй 0,3. Игрок вначале покупает билет первой лотереи. Составить закон распределения случайной величины Х – числа купленных билетов, если он имеет возможность купить только 5 билетов. Найти математическое ожидание случайной величины Х. 10 На спортивных соревнованиях необходимо преодолеть четыре препятствия с вероятностями, равными соответственно 0,9; 0,8; 0,7; 0,6. При первой неудаче спортсмен в дальнейших состязаниях не участвует. Составить закон распределения случайной величины Х – числа взятых препятствий. Найти математическое ожидание случайной величины Х. 11 Имеется 10 билетов: 1 билет в партер стоимостью 2500 руб., 3 билета в амфитеатр по 1000 руб. и 6 билетов на балкон по 300 руб. После реализации части билетов осталось три билета. Составить закон распределения случайной величины Х – стоимости непроданных билетов. Найти математическое ожидание случайной величины Х. 12 Две компании участвуют в аукционе по реализации трех инвестиционных проектов. Вероятность выиграть аукцион для первой компании по первому проекту составляет 0,6, по второму – 0,95 и по третьему проекту 0,4. Возможная прибыль от реализации каждого проекта составляет 12 млн. руб. Определить ожидаемую прибыль для каждой компании. 13 Вероятность успешной сдачи экзамена первым студентом составляет 0,7, а вторым 0,8. Составить закон распределения случайной величины Х – числа студентов, успешно сдавших экзамен, если каждый из них может пересдать один раз экзамен, если он его первый раз не сдал. Найти математическое ожидание случайной величины Х. 14 Дискретная случайная величина Х задана законом распределения:
По одному варианту построить многоугольник распределения. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 15 Предприниматель рассматривает возможность покупки акций трех предприятий, по каждой из которых известна доходность, как отношение величины получаемого дохода за период времени к цене акции и вероятности возможных значений доходности.
Акции какого предприятия следует считать более доходными, если руководствоваться средним значением (математическим ожиданием) доходности. Акции какого предприятия являются менее рискованными (считая, что чем выше колеблемость доходности акций, тем больше их рискованность). 16 Бросают 12 игральных костей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х – суммы числа очков, которые могут появиться на всех выпавших гранях. 17 Математическое ожидание случайной величины Х равно 8. Найти математическое ожидание случайных величин: а) Х-4; б) Х+6; в) 3Х-4; г) 4Х+3. 18 Дисперсия случайной величины Х равна 8. Найти дисперсию следующих величин: а) Х-2; б) Х+6; в) 3Х-2; г) 2Х+7. 19 Найти математическое ожидание и дисперсию случайных величин: а) Z = 4Х-2У; б) Z = 2Х-4У; в) Z = 3Х+5У; г) Z = 0,5Х+3У, если М(Х)=5, М(У) = 3, D(Х) = 4, D(У) = 6. Случайные величины Х и У независимы. 20 Случайные величины Х и У независимы. Найти математическое ожидание и дисперсию случайных величин: а) Z = 4Х+2У; б) Z = 5Х-3У; в) Z = 3Х-У, г) Z = 2Х + 4У, если М(Х) = 6, М(У)= 5, D(Х)= 7, D(У)= 4. 21 Вероятность изготовления бракованной детали автоматом равна 0,002. Найти математическое ожидание и среднее квадратическое отклонение случайной величины Х - числа бракованных деталей, если деталей изготовлено 1000. Определить вероятность того, что из 1000 деталей будет изготовлено: а) не более двух бракованных; б) хотя бы одна бракованная. 22 Независимые случайные величины Х и У имеют следующие распределения:
Составить закон распределения случайных величин: а) Z=Х+У; б) V=ХУ. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайных величин Z и V. 23 В бригаде два звена тракторов. В первом звене 3 трактора, причем вероятность безотказной работы каждого из них в течение смены равна 0,9. Во втором звене 2 трактора, вероятность безотказной работы первого из них равна 0,8, а второго 0,7. Составить закон распределения случайной величины Х – числа тракторов, работавших безотказно в бригаде. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 24 Два стрелка производят по одному выстрелу по мишени. Вероятность поражения мишени первым стрелком равна N: (N+5), вторым N: (N+2). Составить закон распределения случайной величины Z=Х+У, где Х - число поражений мишени первым стрелком, У – число поражений мишени вторым стрелком. Найти числовые характеристики случайной величины Z. 25 Случайные величины Х – площадь посева овощей на хозяйство (га) и У – урожайность овощей с 1 га (т) имеют следующие распределения:
Определить средний валовой сбор овощей на хозяйство, дисперсию и среднее квадратическое отклонение валового сбора овощей. 26 Два независимо работающих станка могут выпускать бракованные изделия за 1 час в соответствии со следующими законами распределения: 1 станок 2 станок
Найти закон распределения случайной величины Z – числа единиц выпуска бракованных изделий для двух одновременно работающих станков. Построить график распределения случайной величины Z. Найти M(Z), D(Z), σ(Z). 27 В учреждении заработная плата служащих на начало января текущего года имела следующий закон распределения:
где x – величина заработной платы для определенной категории служащих, руб.; р – доля служащих определенной категории. В первом полугодии заработную плату повысили на 30 %, во втором полугодии заработная плата выросла по каждой категории служащих на 300 руб. Cоставить закон распределения случайной величины У - заработной платы на конец года. Определить изменение среднего уровня заработной платы за год. 28 Дискретная случайная величина Х принимает три возможных значения: х1=1 с вероятностью р1=0,2; х3=5 с вероятностью 0,3 и х2 с вероятностью р2. Найти х2 и р2, если известно, что М (Х)=3. 29 Вероятность сдать экзамен студентом на «отлично» равна 0,3, на «хорошо» – 0,4. Определить вероятности получения других оценок (2;3), если известно, что М(Х)=3,9. 30 Вероятность выигрыша по лотерейному билету составляет 0,02. Найти М(Х) и 31 По одному тиражу лотереи куплено 100 билетов. Среднее квадратическое отклонение числа выигранных билетов равно трем. Найти вероятность выигрыша по одному билету лотереи. 32 Подброшены две игральные кости. Найти М(Х), где Х - случайная величина – сумма числа очков, которые могут появиться на двух выпавших гранях. 33 Хозяйство продает крупный рогатый скот живым весом х1 и х2 (х2 > x1). Вероятность того, что крупный рогатый скот будет продан весом х1 равна 0,4. Найти закон распределения случайной величины Х – веса крупного рогатого скота, если математическое ожидание составило 4,60 ц, а дисперсия 0,24. 34 Совокупность семей имеет следующее распределение по числу детей:
Определить х1, х2, р2, если известно, что М(Х)=2, D(Х)=0,9. 35 Дискретная случайная величина Х задана законом распределения:
Найти х2, х3, р2, если известно, что М(Х)=4, М(Х2)=20,2. 36 Совокупность студентов имеет следующее распределение по результатам сдачи сессии:
Найти вероятности получения удовлетворительных, хороших и отличных оценок, если известно, что математическое ожидание (среднее значение) результатов сдачи экзаменов составило 3,7, а среднее квадратическое отклонение 0,9. 37 По данным задачи 14 определить модальное и медианное значения случайной величины Х, коэффициенты асимметрии и эксцесса. 38 По данным задачи 25 определить модальное и медианное значение валового сбора, коэффициенты асимметрии и эксцесса.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1959; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.118.36 (0.012 с.) |

 .
.
 . (4.1)
. (4.1)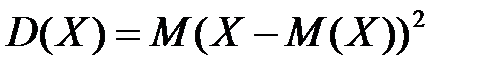 или
или  , (4.2)
, (4.2) . (4.3)
. (4.3) .
. ,
,  (4.4)
(4.4)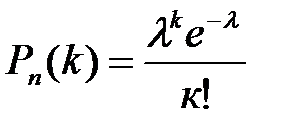 , где
, где  ,
,  ,
,  . (4.5)
. (4.5) (Х) - числа выигранных билетов, если их было приобретено 100.
(Х) - числа выигранных билетов, если их было приобретено 100.


