
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики случайной величиныСодержание книги
Поиск на нашем сайте Задание закона распределения аналитически - с помощью функций F(x) или f(x) позволяет полностью и однозначно описать случайную величину. Но во многих случаях в этом либо нет необходимости, либо закон распределения бывает неизвестен. Тогда ограничиваются меньшими сведениями, а именно некоторыми характерными неслучайными числами, каждое из которых характеризует то или иное свойство распределения случайной величины. Такие числа, позволяющие отразить наиболее существенные особен-ности распределения случайной величины, называются числовыми харак-теристиками случайной величины. Важнейшими из них являются мате-матическое ожидание и дисперсия. Математическим ожиданием (или средним значением) дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на соответствуюшие им вероятности
M(X) называют еще центром распределения или характеристикой положения случайной величины на числовой оси. Это среднее значение, вокруг которого группируются остальные возможные значения случайной величины. Для непрерывной случайной величины
Если возможные значения непрерывной случайной величины
Свойства М (Х) 1. М(С) = С, где С = const. 2. М(СХ) = С М(Х). 3. 4. Для независимых случайных величин X,Y Дисперсия - это характеристика рассеивания (разбросанности) возможных значений случайной величины относительно ее среднего зна-чения. Она определяется как математическое ожидание квадрата отклоне-ния случайной величины от ее математического ожидания
Для вычисления дисперсии удобно пользоваться формулой D(X) = M(X2) – M2 (X). Для дискретных случайных величин для непрерывных случайных величин
Если возможные значения X принадлежат интервалу
Свойства D(X) 1. D(C) = 0, так как постоянная величина C рассеивания не имеет. 2. D(CX) = C2 D(X), то есть постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат. 3. Дисперсия имеет размерность, равную квадрату размерности случайной величины X, что неудобно. Поэтому на практике часто применяют числовую характеристику Пример. Производится одно испытание. Вероятность появления со-бытия A в этом испытании равна p. Найти математическое ожидание и дис-персию числа появлений события A. Решение. Число появлений события A при одном испытании X – дис-кретная случайная величина, ряд распределения которой имеет вид
Поэтому
Пример. Независимые случайные величины X и Y заданы рядами распределения:
Найти среднее квадратичное отклонение случайной величины Решение. По свойствам дисперсии
Так как сумма вероятностей возможных значений случайной вели-чины равна единице, то
По определению дисперсии
Составим ряды распределения случайных величин
Поэтому
Следовательно,
Пример. Случайная величина X задана рядом распределения
Найти дисперсию случайной величины Z = 3X2 - 2X + 1. Решение. Так как случайные величины X и X2 не являются независимыми, то составляем ряд распределения случайной величины Z:
Поэтому ряд распределения Z2 будет иметь вид
В результате получим
Кроме основных характеристик распределения – центра (математического ожидания) и рассеивания (дисперсии) на практике часто нужно описать и другие важные числовые характеристики распределения. Наиболее употребительные из них: мода, медиана, коэффициенты асимметрии, эксцесса. Модой дискретной случайной величины называется ее наиболее вероятное значение, модой непрерывной случайной величины - то ее значение, при котором плотность вероятности максимальна. Медианой В случае симметричного распределения медиана, математическое ожидание и мода совпадают. Для характеристики асимметрии (или “скошенности”) распределения используется величина “ коэффициента асимметрии ’
где В общем случае в теории вероятностей центральным моментом k –го порядка случайной величины X называется математическое ожидание k –ой степени так называемой центрированной случайной величины
Поэтому третий центральный момент равен для дискретной случайной величины для непрерывной случайной величины Если распределение симметрично относительно среднего значения, то “ Крутовершинность ” (или островершинность, плосковершинность) распределения характеризуется величиной эксцесса
где
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

 .
.
 то
то



 ,
,
 то
то
 - для независимых случайных величин.
- для независимых случайных величин. , размерность которой совпадает с размерностью X. Величина
, размерность которой совпадает с размерностью X. Величина 

 .
.











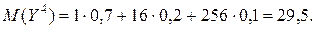



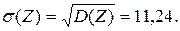
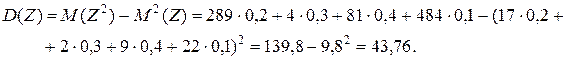
 случайной величины называется такое ее значение, для которого
случайной величины называется такое ее значение, для которого 

 - третий центральный момент.
- третий центральный момент.





 - четвертый центральный момент [3]. Для наиболее распространенного нормального закона распределения (см. ниже), который является как бы эталоном, с которым сравнивают другие распределения,
- четвертый центральный момент [3]. Для наиболее распространенного нормального закона распределения (см. ниже), который является как бы эталоном, с которым сравнивают другие распределения, 



