
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы корреляционного анализаСодержание книги
Поиск на нашем сайте
Как известно, если величины Х и У связаны между собой функциональной зависимостью, то зная значение одной величины, можно точно указать значение другой. В теории вероятностей и в математической статистике рассматривается другой, более общий тип зависимости между величинами, а именно, так называемая статистическая (вероятностная) зависимость. Статистической называется зависимость между переменными вели-чинами Х и У, при которой каждому значению одной величины Х соответ-ствует определенное распределение другой величины У, зависящее от того, какое значение приняла величина Х. В частности, если при изменении одной из величин изменяется среднее значение другой, то такая статистическая зависимость называется корреля-ционной. Определение степени зависимости между случайными величинами по эмпирическим данным и является целью корреляционного анализа. Для простоты будет рассмотрена зависимость между двумя случайными величинами. Если исследуется связь между несколькими случайными величинами, то говорят о множественной корреляции. 10.1. Корреляционная таблица Пусть произведено достаточно большое число независимых опытов над системой случайных величин (Х, У), причем одно и то же значение Корреляционная таблица для двух переменных в общем случае имеет вид:
Таблица 12
В первой строке таблицы 12 указаны наблюдавшиеся значения случайной величины X, , в первом столбце – все наблюдавшиеся значения Y. Если число их велико, то каждый из интервалов, в котором заключены наблюдавшиеся значения Очевидно, сумма частот j -го столбца
Сумма частот i - ой строки Сумма всех частот (общее число наблюдений) равна
и помещается в правом нижнем углу таблицы. Общие средние арифметические переменных x и y равны соответственно
Корреляционная таблица наглядно показывает распределение значения Y для каждого значения X (и наоборот) и является статистическим аналогом таблицы распределения вероятностей системы двух случайных величин. Рассмотрим, например, распределение значений Y при X = xj (см. таблицу 13) Таблица 13
Средняя арифметическая этого распределения называется условной (групповой) средней переменной Y для данного значения xj и обозначается через
Каждому отдельному значению x j переменной X соответствует вполне определенное значение условной средней Аналогично, средняя арифметическая всех наблюдавшихся значений X при условии Y = y i называется условной (групповой) средней переменной X для данного значения y i:
причем Условные средние являются статистическим аналогом условных математических ожиданий в теории вероятностей. Уравнение Двумя основными задачами теории корреляции являются: - изучение зависимости условных средних - оценка силы (тесноты) корреляционной зависимости между величинами X и Y. Отыскание приближенной линии регрессии По эмпирическим данным Отметим, прежде всего, одно важное свойство линии регрессии. Можно показать, что справедлива следующая теорема: среднее значение суммы квадратов отклонений По опытным данным можно построить эмпирическую (“истинную”) линию регрессии, но она представляет собой ломаную линию, и уравнение еë для практического использования непригодно. Поэтому обычно строят приближенную (теоретическую) линию регрессии того или иного вида, определяя неизвестные параметры этой функции из условия минимума D. Можно показать, что если переменные X и Y представляют собой суммы большого числа независимых (или почти независимых) случайных величин, то X и Y связаны линейной корреляционной зависимостью (если она вообще существует). Так как на практике именно этот случай реализуется чаще всего, то приближенную функцию регрессии ищут, как правило, в виде линейной функции Метод наименьших квадратов Суть метода состоит в следующем: пусть известны результаты эксперимента (x 1, y 1), (x 2, y 2),...,(x n, y n) и выбран с точностью до k неизвестных параметров вид функции y = f (x, a 1, a 2,..., a k), (10.4) аппроксимирующей экспериментальные данные. Согласно методу наименьших квадратов неизвестные параметры a i выбираются так, чтобы сумма квадратов отклонений была минимальной
Под отклонением понимается разность между наблюдавшимся значением y i и расчетным значением y, вычисленным по уравнению (10.4) при x=xi. Для отыскания значений
Здесь числа В интересующем нас случае функция
где
В результате получим два линейных уравнения
или
Так как
с учетом обозначений (10.1), (10.2) можно записать
откуда следует:
Функция
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.5.131 (0.008 с.) |

 наблюдалось
наблюдалось  раз (j = 1, 2,..., t), одно и то же значение
раз (j = 1, 2,..., t), одно и то же значение  раз (i = 1, 2, …, s), каждая пара значений
раз (i = 1, 2, …, s), каждая пара значений  наблюдалась
наблюдалась 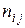 раз (отдельные значения
раз (отдельные значения 
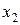



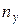
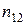




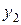


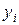


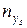
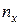
 .
.
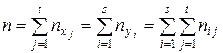 (10.1)
(10.1) ,
, .
. . Очевидно, что
. Очевидно, что
 (10.2)
(10.2) переменной Y, то есть
переменной Y, то есть  Следовательно, статистическая зависимость между
Следовательно, статистическая зависимость между  (i =1,2,... ,s), (10.3)
(i =1,2,... ,s), (10.3) .
. называется выборочным (или эмпирическим) уравнением регрессии Y на X, функция f (x) называется выборочной регрессией Y на X, а ее график – выборочной линией регрессии Y на X. Аналогично, уравнение
называется выборочным (или эмпирическим) уравнением регрессии Y на X, функция f (x) называется выборочной регрессией Y на X, а ее график – выборочной линией регрессии Y на X. Аналогично, уравнение  - выборочной регрессией X на Y, а ее график – выборочной линией регрессии X на Y.
- выборочной регрессией X на Y, а ее график – выборочной линией регрессии X на Y. от Y), то есть установление вида функции регрессии,
от Y), то есть установление вида функции регрессии, величин y i от выборочной линии регрессии
величин y i от выборочной линии регрессии  При этом задача сводится лишь к отысканию неизвестных параметров a и в. Это можно сделать различными способами. Наиболее распространенным из них, позволяющим получить в некотором смысле наилучшее приближение к экспериментальным данным, является метод наименьших квадратов.
При этом задача сводится лишь к отысканию неизвестных параметров a и в. Это можно сделать различными способами. Наиболее распространенным из них, позволяющим получить в некотором смысле наилучшее приближение к экспериментальным данным, является метод наименьших квадратов. . (10.5)
. (10.5) обеспечивающих минимум левой части уравнения (10.5), необходимо приравнять нулю производные по
обеспечивающих минимум левой части уравнения (10.5), необходимо приравнять нулю производные по  Тогда получим
Тогда получим (10.6)
(10.6) - значения частных производных функции по параметрам
- значения частных производных функции по параметрам  в точке x i. Число уравнений в системе (10.6) равно числу неизвестных параметров.
в точке x i. Число уравнений в системе (10.6) равно числу неизвестных параметров. линейна и содержит два неизвестных параметра. Необходимыми условиями минимума суммы квадратов отклонений условных средних (то есть “истинной” линии регрессии) от приближенной функции регрессии являются условия
линейна и содержит два неизвестных параметра. Необходимыми условиями минимума суммы квадратов отклонений условных средних (то есть “истинной” линии регрессии) от приближенной функции регрессии являются условия

 .
.


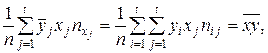



 . (10.7)
. (10.7) , коэффициенты которой определяются по формуле (10.7), называется линейной среднеквадратической регрессией Y на X.
, коэффициенты которой определяются по формуле (10.7), называется линейной среднеквадратической регрессией Y на X.


