
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства коэффициента корреляцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Если между величинами X и Y существует линейная функциональная связь
то Действительно, Но Cледовательно, Равенство 2. Чем больше угол между линиями регрессии У на Х и Х на У, тем меньше
Очевидно,
Итак, с уменьшением При 3. При 4. Если коэффициент корреляции
При достаточно большом n (практически при 10.6. Методика вычисления Методику вычислений Пример. Результаты измерений угловых колебаний ведущего моста автомобиля X и угловых колебаний подрессоренной массы (галопирование) Y сведены в корреляционную таблицу 14. Найти уравнение линейной среднеквадратической регрессии Y на X, установить тесноту связи между признаками. Для каждого интервала значений X вычислить фактические значения условных средних Расчет может быть значительно упрощен, если перейти от величин X и Y к условным вариантам по формулам
Легко убедиться в том, что при этом
Поэтому выборочный коэффициент корреляции
Трудоемкость расчета связана с вычислением В качестве ложного нуля
соседними вариантами:
Таблица 14
Величины
аналогично
Искомый коэффициент корреляции равен
Возвращаясь к старым переменным, получим
или окончательно
Фактические значения условных средних, вычисленные по данным корреляционной таблицы, равны:
Аналогично
Эти значения, а также условные средние, найденные по уравнению регрессии (10.12) при Таблица 15
Как видно из таблицы, согласование фактически наблюдавшихся и расчетных условных средних удовлетворительное. Эмпирическая и приближенная (теоретическая) линии регрессии Y на X показаны на рисунке.
Р А С Ч Е Т Н О – Г Р А Ф И Ч Е С К А Я Р А Б О Т А П О Т Е О Р И И В Е Р О Я Т Н О С Т Е Й ВАРИАНТ 1 1. В урне 4 черных, 6 белых и 5 красных шаров. Наудачу извлечены 7 шаров. Найти вероятность того, что среди них окажутся 2 черных, 3 белых и 2 красных шара. 2. Рабочий обслуживает 3 станка. Вероятность того, что в течение смены первый станок потребует его внимания, равна 0,2; второй - 0,25, третий - 0,3. Найти вероятность того, что в течение смены внимания рабочего потребуют какие-либо два станка; все три станка. 3. Вероятности безотказной работы элементов электрической цепи равны соответственно
4. Три станка подают детали в общий бункер. Вероятность выпуска бракованной продукции для первого станка 0,03, для второго - 0,02 и для третьего - 0,01. Производительность первого станка в 3 раза больше производительности второго, а производительность третьего в два раза больше, чем у второго. Какова вероятность того, что взятая наудачу деталь из бункера окажется годной? 5. Вероятность надежной работы конструкции при приложении расчетной нагрузки равна 0,96. Найти вероятность того, что из 10 конструкций, испытанных независимо друг от друга, больше двух выйдут из строя. 6. Вероятность выхода из строя каждого из 900 независимо работающих элементов некоторого узла в течение заданного времени равна 0,1. Найти вероятность того, что по истечении заданного времени будут работать 800 элементов; будут работать от 800 до 850 элементов. 7. В бригаде 8 рабочих, из них 5 учатся. Наудачу по списку отобраны 3 человека. Составить закон распределения дискретной случайной величины Х - числа рабочих, которые учатся, среди рабочих. 8. Случайная величина X задана рядом распределения
Найти математическое ожидание и дисперсию случайной величины
9. Завод отправил на базу 2000 изделий. Вероятность повреждения изделия в пути равна 0,0015. Найти вероятность того, что в пути будет повреждено: хотя бы одно изделие; не более одного изделия. 10. Плотность вероятностей случайной величины X равна
Найти интегральную функцию распределения F(x), M(X), D (X) и ве- роятность P(a<X<1,5a). 11. Диаметр детали - нормально распределенная случайная величина с параметрами: ВАРИАНТ 2 1. В партии из 7 деталей 5 стандартных. Наудачу отобраны 3 детали. Какова вероятность того, что среди них 2 детали стандартны? 2. В поисках нужной книги студент опрашивает 3-х товарищей. Вероятности получить нужную книгу у 1-го, 2-го, 3-го товарищей соответственно равны 0,3, 0,4, 0,5. Определить вероятность того, что студент получит книгу у одного из товарищей. 3. Вероятность работы каждого из независимо работающих элементов электрической цепи
4. Часы изготавливаютcя на трех заводах и поступают в магазин. Первый завод производит 40% всей продукции, второй - 35%, третий - 25%. Из продукции первого завода спешат 10 % часов, у второго – 15 %, у третьего – 20 %. Какова вероятность того, что купленные часы спешат? 5. Вероятность выхода из строя конструкции при приложении расчетной нагрузки 0,05. Какова вероятность того, что из восьми конструкций, испытанных независимо друг от друга, не менее шести выдержат нагрузку?
6. Произведено 100 выстрелов, вероятность попадания при одном выстреле – 0,95. Найти вероятность того, что попали 96 раз; не менее 96 раз. 7. Устройство состоит из четырех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,2. Составить закон распределения случайной величины Х - числа работающих элементов в одном опыте. 8. Независимые случайные величины X и Y заданы рядами распределения. Найти дисперсию случайной величины
9. Завод отправил на базу 2000 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что будет повреждено не более трех изделий. 10. Плотность вероятностей случайной величины Х равна
Найти коэффициент "с ", интегральную функцию распределения F(x), M (X), D(X) и вероятность P(1,5<X<2). 11. Автомат штампует детали. Контролируется длина детали Х, которая распределена по нормальному закону с математическим ожиданием (проектная длина) ВАРИАНТ 3 1. В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных окажутся три женщины. 2. Вероятности того, что нужная сборщику деталь содержится в первом, втором, третьем или четвертом ящиках соответственно равны: 0,6; 0,7; 0,8; 0,9. Найти вероятность того, что нужная деталь содержится не менее чем в двух ящиках. 3. Найти вероятность безотказной работы электрической цепи, состоящей из независимо работающих элементов, если вероятность работы каждого элемента равна P=0,9.
4. На автобазе имеется 80 грузовых и 20 легковых автомашин. Вероятность того, что грузовая машина неисправна, равна 0,08, а легковая - 0,05. Найти вероятность того, что наудачу по номеру вызванная автомашина окажется исправной. 5. Произведено 12 независимых выстрелов по цели. Вероятность попадания при одном выстреле равна 0,85. Найти вероятность того, что будет не менее двух промахов в цель. 6. Событие B появится в том случае, если событие A наступит не менее 150 раз. Найти вероятность появления события B, если произведено 200 независимых испытаний, в каждом из которых вероятность появления события A равна 0,7.
7. На складе имеются 8 покрышек, из них 3 - изношенных. Наудачу отобраны 3 покрышки. Составить закон распределения дискретной случайной величины X - числа годных покрышек среди отобранных. 8. Случайная величина X задана рядом распределения. Найти математическое ожидание и дисперсию величины
9. Плотность вероятностей случайной величины Х равна
Найти коэффициент "а", интегральную функцию распределения F(x), M (X), D(X) и вероятность P(1<X<1,5). 11. Aвтомат штампует детали. Контролируется длина детали Х, которая распределена по нормальному закону с математическим ожиданием (проектная длина) ВАРИАНТ 4 1. В группе 16 студентов, среди которых 4 отличника. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов 3 отличника. 2. ОТК проверяет изделия на соответствие стандарту. Вероятность того, что первое изделие стандартно, равна 0,8, второе - 0,9, третье - 0,95. Найти вероятность того, что из трех проверенных изделий только одно стандартно; хотя бы одно стандартно. 3. Электрическая цепь состоит из последовательно и параллельно соединенных элементов, работающих независимо. Вероятности работы каждого из элементов равны
4. В первой урне 10 шаров, из них 8 белых; во второй - 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих шаров взяли один шар. Найти вероятность того, что этот шар белый. 5. Вероятность безотказной работы каждого из семи независимо работающих элементов некоторого устройства равна 0,85. Найти вероятность того, что выйдут из строя не более трех элементов. 6. Испытывается каждый из 120 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти вероятность того, что выдержат испытание ровно 110 элементов; более 110 элементов. 7. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. Составить закон распределения числа библиотек, которые посетит студент, если в городе 4 библиотеки. 8. Независимые случайные величины X и Y заданы рядами распределения
Найти дисперсию случайной величины 9. Автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,002. Найти вероятность того, что среди 500 деталей окажется хотя бы одна бракованная; не более одной бракованной.
10. Плотность вероятностей случайной величины X равна
Найти коэффициент " M(X), D(X) и вероятность P(0,5<X<1). 11. Диаметр детали - нормально распределенная случайная величина X с параметрами: ВАРИАНТ 5 1. В ящике 10 деталей, среди которых 7 окрашенных. Сборщик наудачу извлекает 4 детали. Найти вероятность того, что 2 детали среди извлеченных окажутся окрашенными. 2. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что одно из трех наудачу взятых изделий окажется высшего сорта, равна 0,85, другое - 0,95, третье - 0,75. Найти вероятность того, что из трех проверенных изделий не менее двух будут высшего сорта. 3. Найти вероятность безотказной работы электрической цепи, изображенной на рисунке, если вероятность отказа каждого из независимо работающих элементов равна 0,15.
4. Три цеха производят одинаковые детали, которые поступают на общую сборку. Вероятность изготовления стандартной детали в первом цехе - 0,93, во втором - 0,88, в третьем - 0,85. Первый цех имеет три технологические линии, второй - две, третий - одну (линии одинаковой производительности). Найти вероятность того, что наудачу взятая деталь на сборке окажется нестандартной. 5. Вероятность выхода из строя каждого из 9 независимо работающих элементов некоторого узла в течение времени t равна 0,1. Найти вероятность того, что по истечении времени t будут работать не менее 7 элементов. 6. Электрическая цепь состоит из 100 параллельно включенных потребителей. Вероятность надежной работы каждого из них 0,9, а взаимное влияние в цепи отсутствует. Найти вероятность того, что откажет менее 5% от общего числа потребителей; ровно 5% потребителей. 7. В комплекте из 12 изделий имеются 8 изделий первого сорта и 4 второго. Наудачу отобраны 3 изделия. Составить закон распределения дискретной случайной величины Х - числа изделий второго сорта среди отобранных. 8. Дискретная случайная величина Х задана рядом распределения. Найти математическое ожидание и дисперсию величины
9. Коммутатор учреждения обслуживает 200 абонентов. Вероятность того, что в течение одной минуты абонент позвонит на коммутатор, равна 0,02. Найти вероятность того, что в течение одной минуты позвонит хотя бы один абонент; не более одного абонента. 10. Плотность вероятностей случайной величины Х равна
Найти коэффициент “ M(X), D(X) и вероятность P(0<X<π/12). 11. Автомат штампует детали. Контролируется длина детали Х, которая распределена по нормальному закону с математическим ожиданием (проектная длина) ВАРИАНТ 6 1. На складе имеются 10 покрышек, из них 2 изношенных. Найти вероятность того, что среди взятых наудачу 5 покрышек окажутся 4 годных. 2. Неисправность может возникнуть в одном из 4-х блоков устройства. Вероятность возникновения неисправности в первом блоке равна 0,20, во втором - 0,15, в третьем и в четвертом - 0,10. Найти вероятность появления неисправности только в одном блоке; хотя бы в одном блоке. 3. Найти вероятность работы электрической цепи, изображенной на рисунке, если вероятность отказа каждого из независимо работающих элементов равна 0,1.
4. На сборке находятся детали, изготовленные на 3-х конвейерах, причем деталей, изготовленных на первом конвейере вдвое больше, чем изготовленных на втором конвейере и в 1,5 раза больше, чем изготовленных на третьем. Вероятности того, что деталь высокого качества, равны 0,8 для первого конвейера, 0,75 - для второго конвейера и 0,7 для третьего. Найти вероятность того, что наудачу взятая деталь на сборке будет высокого качества. 5. Произведено 10 выстрелов, вероятность попадания при одном выстреле 0,9. Найти вероятность не менее 8 попаданий. 6. Автотранспортное предприятие имеет 180 автобусов. Вероятность выхода на линию каждого автобуса равна 0,9. Найти вероятность нормальной работы предприятия в ближайший день, если для этого необходимо иметь на линии не менее 160 автобусов, ровно 160 автобусов. 7. Найти закон распределения дискретной случайной величины X - числа появлений шестерки при четырех подбрасываниях игральной кости. 8. Независимые случайные величины X и Y заданы рядами распределения
Найти дисперсию случайной величины 9. Коммутатор учреждения обслуживает 100 абонентов. Вероятность того, что в течение одной минуты абонент позвонит на коммутатор, равна 0,01. Найти вероятность того, что в течение одной минуты позвонят менее трех абонентов. 10. Плотность вероятностей случайной величины Х равна
Найти коэффициент “ M(X), D(X) и вероятность P(0,5<X<1,5). 11. На станке изготавливается деталь. Ее длина Х - случайная величина, распределенная по нормальному закону с параметрами ВАРИАНТ 7 1. В комплекте 12 деталей 1-го сорта и 6 - второго. Наудачу вынимаются 4 детали. Найти вероятность того, что среди них окажутся 3 детали первого сорта. 2. В урне 5 белых и 4 красных шара, одинаковых на ощупь. Наудачу вынимаются 3 шара. Найти вероятность того, что среди извлеченных шаров будет не менее двух красных. 3. Найти вероятность безотказной работы электрической цепи, coстоящей из независимо работающих элементов, если вероятность работы каждого элемента равна 0,98.
4. Комплект состоит из 16 деталей завода № 1, 12 деталей завода № 2 и 22 деталей завода № 3. Вероятности того, что деталь низкого качества соответственно равны 0,08 для первого завода, 0,06 - для второго завода и 0,1 для третьего. Найти вероятность того, что наудачу вынутая деталь из комплекта будет высокого качества. 5. Событие В появится в том случае, если событие А наступит не менее двух раз. Найти вероятность появления события В, если произведено шесть независимых испытаний, в каждом из которых вероятность появления события А равна 0,4. 6. Автобаза обслуживает 140 магазинов. От каждого из них заявка на автомашины на следующий день может поступить с вероятностью 0,7. Найти вероятность того, что поступит не менее 110 и не более 120 заявок; ровно 110 заявок. 7. В команде 9 спортсменов, из них 4 - первого разряда и 5 - второго. Наудачу отобраны 3 спортсмена. Найти ряд распределения дискретной случайной величины Х - числа спортсменов второго разряда среди отобранных. 8. Дискретная случайная величина X задана рядом распределения
Найти 9. Коммутатор учреждения обслуживает 200 абонентов. Вероятность того, что в течение одной минуты абонент позвонит на коммутатор, равна 0,01. Найти вероятность того, что в течение минуты позвонят более двух абонентов. 10. Плотность вероятностей случайной величины Х равна
Найти коэффициент “ M(X), D(X) и вероятность 11. На станке изготавливается деталь. Ее длина Х - случайная величина, распределенная по нормальному закону с параметрами ВАРИАНТ 8 1. В партии 8 изделий первого сорта и 7 второго. Найти вероятность того, что среди наудачу выбранных 6 изделий окажутся 3 изделия первого сорта. 2. В урне 7 белых и 5 красных шаров, одинаковых на ощупь. Наудачу извлекаются 4 шара. Найти вероятность того, что среди них будет не менее трех красных. 3. Найти вероятность работы электрической цепи, изображенной на рисунке, если вероятность отказа каждого из независимо работающих элементов равна 0,1.
4. В коробке 10 деталей завода № 1, 15 деталей завода № 2 и 25 деталей завода №3. Вероятности того, что деталь высокого качества равны соответственно 0,95 для первого завода, 0,85 для второго и 0,7 для третьего. Найти вероятность того, что наудачу вынутая деталь из коробки будет высокого качества. 5. Испытывается каждый из 12 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, которое выдержит испытание и его вероятность; вероятность того, что выдержат испытание более 9 элементов. 6. Две равносильные ЭВМ играют шахматный матч. Что вероятнее: выиграть (ничейный результат исключается) не менее двух партий из четырёх, от 20 до 30 партий из 40 или ровно 20 партий из 40? 7. Написать закон распределения числа появлений герба при четырех подбрасываниях монеты. 8. Независимые случайные величины X и Y заданы рядами распределения
Найти дисперсию случайной величины 9. Учебник издан тиражом 200000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,00001. Найти вероятность того, что тираж содержит ровно две бракованные книги; не более двух бракованных книг. 10. Плотность вероятностей случайной величины X равна
Найти коэффициент “ M(X), D(X) и вероятность P(0<X<π/6). 11. Автомат штампует детали. Контролируется длина детали X, которая распределена по нормальному закону с математическим ожиданием (проектная длина) ВАРИАНТ 9 1. Cреди 17 студентов группы, из которых 8 девушек, разыгрываются 7 билетов, причем каждый может выиграть только один билет. Какова вероятность того, что среди обладателей билетов окажутся 4 девушки? 2. В урне 4 белых и 6 красных шаров. Наудачу извлекаются 3 шара. Найти вероятность того, что среди них окажется менее двух красных шаров. 3. Найти вероятность безотказной работы электрической цепи, состоящей из независимо работающих элементов, если вероятность работы каждого элемента равна 0,95.
4. Два завода выпускают одинаковые изделия. Вероятность брака для 1-го завода равна 0,05, для 2-го - 0,10. Первый завод имеет два конвейера; второй - один конвейер. Детали с заводов поступают на склад. Найти вероятность того, что наудачу взятая на складе деталь будет годной. 5. Электрическая цепь состоит из 7 параллельно включенных потребителей. Вероятность надежной работы каждого из них 0,9, а взаимное влияние в цепи отсутствует. Найти вероятность того, что откажет менее половины потребителей. 6. Что вероятнее - выиграть у равносильного противника (ничейный результат исключается) не менее трех партий из пяти, не менее 30 партий из 50 или ровно 30 партий из 50? 7. В команде 11 спортсменов, из них 7 первого разряда и 4 второго. Наудачу выбраны 3 спортсмена. Найти ряд распределения дискретной случайной величины X - числа спортсменов первого разряда среди отобранных. 8. Случайная величина X задана рядом распределения
Найти 9. При штамповке металлических клемм получается в среднем 98% годных. Какова вероятность того, что среди 200 клемм будут две; более двух бракованных? 10. Плотность вероятностей случайной величины X равна
Найти коэффициент " M(X), D(X) и вероятность P(0<X<2π/3). 11. На станке изготавливается деталь. Ее длина Х - случайная величина, распределенная по нормальному закону с параметрами
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 932; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.232.145 (0.012 с.) |



 .
.


 а
а 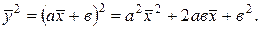
 и
и 
 Это наглядно иллюстрируется рисунком.
Это наглядно иллюстрируется рисунком.

 следовательно,
следовательно, .
. увеличивается
увеличивается 
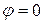
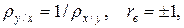 и линии регрессии совпадают между собой и с прямой линейной функциональной зависимости.
и линии регрессии совпадают между собой и с прямой линейной функциональной зависимости.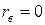 отсутствует линейная корреляционная зависимость между X и Y. Отметим, что при этом может существовать нелинейная связь между X и Y (корреляционная или функциональная).
отсутствует линейная корреляционная зависимость между X и Y. Отметим, что при этом может существовать нелинейная связь между X и Y (корреляционная или функциональная).
 ) для оценки коэффициента корреляции нормально распределенной генеральной совокупности можно пользоваться формулой
) для оценки коэффициента корреляции нормально распределенной генеральной совокупности можно пользоваться формулой 
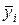 и их значения по уравнению регрессии.
и их значения по уравнению регрессии.


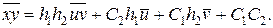

 Для составления корреляционной таблицы в условных вариантах добавим к исходной корреляционной таблице (поле которой выделено толстыми линиями) дополнительные строки
Для составления корреляционной таблицы в условных вариантах добавим к исходной корреляционной таблице (поле которой выделено толстыми линиями) дополнительные строки  и столбцы
и столбцы 
 для X примем находящуюся примерно в середине вариационного ряда для X величину
для X примем находящуюся примерно в середине вариационного ряда для X величину  аналогично принимаем
аналогично принимаем  Шаг
Шаг 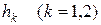 равен разности между двумя
равен разности между двумя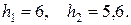 Легко показать, что суммы элементов нижней строки и правого столбца равны между собой:
Легко показать, что суммы элементов нижней строки и правого столбца равны между собой:
 целесообразно вычислять по обеим формулам. Их совпадение должно свидетельствовать о правильности вычислений.
целесообразно вычислять по обеим формулам. Их совпадение должно свидетельствовать о правильности вычислений.







 при большом числе наблюдений подсчитываются методом произведений, а при сравнительно малом числе наблюдений - непосредственно, исходя из определения этих величин по формулам:
при большом числе наблюдений подсчитываются методом произведений, а при сравнительно малом числе наблюдений - непосредственно, исходя из определения этих величин по формулам:
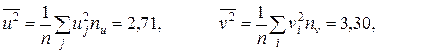



 Приближенное (теоретическое) уравнение линейной регрессии примет вид
Приближенное (теоретическое) уравнение линейной регрессии примет вид
 (10.12)
(10.12)


 приведены ниже в таблице 15:
приведены ниже в таблице 15:




 Найти вероятность отказа цепи.
Найти вероятность отказа цепи.
 .
.
 мм,
мм,  мм. Найти вероятность того, что диаметр наудачу взятой из партии детали составит от 74 мм до 76,4 мм; отличается от "
мм. Найти вероятность того, что диаметр наудачу взятой из партии детали составит от 74 мм до 76,4 мм; отличается от " 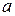 " не более, чем на 1,4 мм. Какое отклонение диаметра от "
" не более, чем на 1,4 мм. Какое отклонение диаметра от "  0,95. Найти вероятность работы цепи.
0,95. Найти вероятность работы цепи.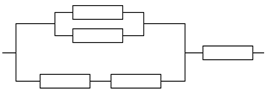
 .
.
 мм. Фактическая длина изготовленных деталей не менее 116,5 мм и не более 123,5 мм. Найти вероятность того, что длина наудачу взятой детали меньше 117,2 мм. Какое отклонение длины детали от математического ожидания можно гарантировать с вероятностью 0,99?
мм. Фактическая длина изготовленных деталей не менее 116,5 мм и не более 123,5 мм. Найти вероятность того, что длина наудачу взятой детали меньше 117,2 мм. Какое отклонение длины детали от математического ожидания можно гарантировать с вероятностью 0,99?


 135 мм. Фактическая длина изготовленных деталей 131< X < 139 мм. Найти вероятность того, что длина наудачу взятой детали меньше 133 мм. Какое отклонение длины детали от "а " можно гарантировать с вероятностью 0,96? В каких пределах с вероятностью 0,9973 будут заключены длины изготовленных деталей?
135 мм. Фактическая длина изготовленных деталей 131< X < 139 мм. Найти вероятность того, что длина наудачу взятой детали меньше 133 мм. Какое отклонение длины детали от "а " можно гарантировать с вероятностью 0,96? В каких пределах с вероятностью 0,9973 будут заключены длины изготовленных деталей?

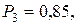

 Найти вероятность работы цепи.
Найти вероятность работы цепи.
 .
.
 ", интегральную функцию распределения F(x),
", интегральную функцию распределения F(x), 1,8 мм. Найти вероятность того, что диаметр наудачу взятой детали из партии составит от 69 мм до 70,9 мм; отличается от "
1,8 мм. Найти вероятность того, что диаметр наудачу взятой детали из партии составит от 69 мм до 70,9 мм; отличается от " 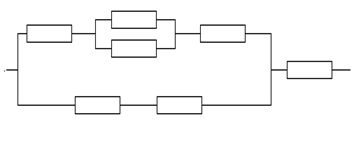


 ”, интегральную функцию распределения F(x),
”, интегральную функцию распределения F(x),
 .
.
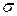 =1,2 см. Найти вероятность того, что длина детали будет заключена между 20 и 21,9 см. Какое отклонение длины детали от "
=1,2 см. Найти вероятность того, что длина детали будет заключена между 20 и 21,9 см. Какое отклонение длины детали от " 
 и
и 



 .
.
 и
и 




