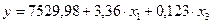Построение уравнений многофакторной корреляционной связи

Общее назначение множественной регрессии состоит в анализе связи между несколькими независимыми переменными и зависимой переменной. В общественных и естественных науках процедуры множественной регрессии чрезвычайно широко используются в исследованиях.

Статическая модель, представленная уравнением регрессии с несколькими переменными величинами, называется многофакторной моделью или множественной регрессией.

Двумя наиболее важными этапами построения многофакторных моделей являются:

· выбор формы связи (уравнения регрессии);

· отбор факторных признаков.

Уравнение множественной регрессии в общем виде записывается:

а - константа (свободный член);

b - угловой коэффициент (регрессионный коэффициент);

Y - зависимая переменная;

Х1, Х2, Х_n – независимые переменные.

Выбор наиболее качественных признаков-факторов для формирования уравнения множественной регрессии вида: y = b ₁ + b ₂ x ₁ + b ₃ x ₂ осуществим по:

· наибольшей представительности;

· наименьшему коэффициенту вариации;

· наибольшему коэффициенту парной корреляции.

Для построения уравнения используем 2 пары факторов: X₁, X₃ и X₂, X₃.

Результатом работы программы является получение коэффициентов регрессии, необходимых для построения уравнения множественной регрессии:

Табл.17

Коэффициенты регрессии при выборе пары факторов X₁, X₃

Коэффициенты регрессии:

---------------------------

| Kn | Значение |

---------------------------

| b1 |.752998E+04 |

---------------------------

| b2 |.335982E+01 |

---------------------------

| b3 |.123001E+00 |

---------------------------

 

 

Табл.18

Коэффициенты регрессии при выборе пары факторов X₂, X₃

Коэффициенты регрессии:

---------------------------

| Kn | Значение |

---------------------------

| b1 |.281109E+04 |

---------------------------

| b2 |.112653E+01 |

---------------------------

| b3 |.146631E+01 |

---------------------------

 

По полученным данным составим 2 уравнения:

1)

2)

Для уточнения надёжности полученных уравнений выбирается контрольный уровень и производится проверка. Программа производит проверку по 11-му уровню:

Табл.19

Проверка надёжности 1-ого уравнения

Расчет абсолютной ошибки:

Итерация равна: 74

Абсолютная ошибка равна:.460520E+03

Относительная ошибка равна: 1.89%

Расчет произведен по 11-му уровню.

 

Ошибка не превышает регламента.

Имитация явления данным уравнением надежна.

Табл.20

Проверка надёжности 2-ого уравнения

Расчет абсолютной ошибки:

Итерация равна: 74

Абсолютная ошибка равна:.877344E+01

Относительная ошибка равна:.04%

Расчет произведен по 11-му уровню.

 

Ошибка не превышает регламента.

Имитация явления данным уравнением надежна.

Уравнение считается корректным, если относительная ошибка не превышает 8 – 15%.

Относительная ошибка в обоих случаях мала, следовательно, полученные уравнения являются корректными и надёжно имитируют динамику признака–функции. Полученные уравнения ( и ) можно использовать в трёхлетней и пятилетней перспективах соответственно.

Заключение

В данной курсовой работе мы провели качественный анализ исходных динамических рядов. Выяснили, что динамическая связь между признаком-функцией и признаками-факторами жесткая, направленность динамики по всем признакам растущая, все признаки-факторы сонаправлены с признаком-функцией. Определение характера связи между признаком-функцией и признаками-факторами показало, что данная балансовая связь представительна.

Для построения уравнения многофакторной корреляционной связи был осуществлен отбор из четырех признаков-факторов двух наиболее качественных.

В итоге были составлены два уравнения множественной регрессии, которые являются корректными и надёжно имитируют динамику признака–функции, поскольку относительная ошибка в обоих случаях не превышает регламента.

Таким образом, можно считать, что цель курсовой работы достигнута.

Список использованной литературы

1. Гусаров В.М. – «Статистика: Учеб. Пособие для вузов» – М.: ЮНИТИ-ДАНА, 2003. – 463 с.

2. Елисеева И.И., Юзбашев М.М. – «Общая теория статистики» – М.: «Финансы и статистика», 2002

3. Харламов А.И. – «Общая теория статистики» - М., 1996. – 296 с.

4. Статистика: Учеб. Пособие для самостоятельной работы студентов/Сост.: В.П. Скобелина, Ю.В. Любек, Е.Г. Катышева. Санкт-Петербургский государственный горный институт (технический университет). СПб, 2005. 73 с.

5. Статистика: Методические указания к курсовой работе/Сост.: В.П. Скобелина, Ю.В. Любек, Е.Г. Катышева. Санкт-Петербургский государственный горный институт (технический университет). СПб, 2010. 16 с.

Приложение 1

Распечатка результатов, полученных с помощью программы «Elvis», учитывающих наличие 4 признаков-факторов (Х1, Х2, Х3, Х4) и признака-функции (У) согласно варианту задания 1 (7.4).

 

ВАРИАНТ НОМЕР:74

Работу выполнил:

Ptokhova Anna

 

Исходные данные:

 

--N------Y----------X1---------X2---------X3---------X4---

 

1. 19532.0 3421.0 9073.0 4466.0 2586.0

2. 19618.0 3723.0 10219.0 3945.0 2710.0

3. 20171.0 3792.0 10407.0 3849.0 2943.0

4. 20932.0 4021.0 10712.0 4480.0 2749.0

5. 22612.0 4316.0 11421.0 4382.0 2693.0

6. 22871.0 4107.0 12103.0 4450.0 2871.0

7. 23214.0 4381.0 13719.0 3212.0 2312.0

8. 25104.0 4507.0 12402.0 5678.0 2877.0

9. 25431.0 4673.0 10312.0 7543.0 2983.0

10. 24719.0 4492.0 8611.0 8399.0 3217.0

11. 24302.0 4527.0 7412.0 8956.0 3409.0

12. 24107.0 4613.0 7206.0 9177.0 3126.0

13. 24010.0 4921.0 7914.0 8204.0 2971.0

14. 22308.0 4617.0 8032.0 6956.0 2763.0

15. 22719.0 4502.0 8171.0 7434.0 2697.0

16. 22534.0 4611.0 8720.0 6300.0 2903.0

17. 22071.0 4307.0 9023.0 6237.0 2718.0

18. 22312.0 4109.0 9912.0 5529.0 2512.0

19. 22581.0 4142.0 9987.0 5681.0 2693.0

20. 22873.0 4111.0 10762.0 5742.0 2914.0

 

Исходные данные в абсолютных величинах:

 

 

--N------Y----------X1---------X2---------X3---------X4---

 

1. 19532.0 3421.0 9073.0 4466.0 2586.0

2. 19618.0 3723.0 10219.0 3945.0 2710.0

3. 20171.0 3792.0 10407.0 3849.0 2943.0

4. 20932.0 4021.0 10712.0 4480.0 2749.0

5. 22612.0 4316.0 11421.0 4382.0 2693.0

6. 22871.0 4107.0 12103.0 4450.0 2871.0

7. 23214.0 4381.0 13719.0 3212.0 2312.0

8. 25104.0 4507.0 12402.0 5678.0 2877.0

9. 25431.0 4673.0 10312.0 7543.0 2983.0

10. 24719.0 4492.0 8611.0 8399.0 3217.0

11. 24302.0 4527.0 7412.0 8956.0 3409.0

12. 24107.0 4613.0 7206.0 9177.0 3126.0

13. 24010.0 4921.0 7914.0 8204.0 2971.0

14. 22308.0 4617.0 8032.0 6956.0 2763.0

15. 22719.0 4502.0 8171.0 7434.0 2697.0

16. 22534.0 4611.0 8720.0 6300.0 2903.0

17. 22071.0 4307.0 9023.0 6237.0 2718.0

18. 22312.0 4109.0 9912.0 5529.0 2512.0

19. 22581.0 4142.0 9987.0 5681.0 2693.0

20. 22873.0 4111.0 10762.0 5742.0 2914.0

 

Одним из условий возможности проведения

анализа динамических рядов является их непрерывность.

В нашем случае ряды непрерывны.

 

За базу принят 1-й уровень.

 

 

Наличие в 3-ей,4-й и 5-й колонке

значений <99.999> говорит о том,что имело место

деление на ноль.

 

Показатели по 1-му признаку:

 

Признак Абсолютные Темпы Темпы Цепные темпы

N1 разности роста прироста роста

19532.0 ------ 1.000.000 -----

19618.0 86.0 1.004.004 1.004

20171.0 553.0 1.033.033 1.028

20932.0 761.0 1.072.072 1.038

22612.0 1680.0 1.158.158 1.080

22871.0 259.0 1.171.171 1.011

23214.0 343.0 1.189.189 1.015

25104.0 1890.0 1.285.285 1.081

25431.0 327.0 1.302.302 1.013

24719.0 -712.0 1.266.266.972

24302.0 -417.0 1.244.244.983

24107.0 -195.0 1.234.234.992

24010.0 -97.0 1.229.229.996

22308.0 -1702.0 1.142.142.929

22719.0 411.0 1.163.163 1.018

22534.0 -185.0 1.154.154.992

22071.0 -463.0 1.130.130.979

22312.0 241.0 1.142.142 1.011

22581.0 269.0 1.156.156 1.012

22873.0 292.0 1.171.171 1.013

 

Показатели по 2-му признаку:

 

Признак Абсолютные Темпы Темпы Цепные темпы

N2 разности роста прироста роста

3421.0 ------ 1.000.000 -----

3723.0 302.0 1.088.088 1.088

3792.0 69.0 1.108.108 1.019

4021.0 229.0 1.175.175 1.060

4316.0 295.0 1.262.262 1.073

4107.0 -209.0 1.201.201.952

4381.0 274.0 1.281.281 1.067

4507.0 126.0 1.317.317 1.029

4673.0 166.0 1.366.366 1.037

4492.0 -181.0 1.313.313.961

4527.0 35.0 1.323.323 1.008

4613.0 86.0 1.348.348 1.019

4921.0 308.0 1.438.438 1.067

4617.0 -304.0 1.350.350.938

4502.0 -115.0 1.316.316.975

4611.0 109.0 1.348.348 1.024

4307.0 -304.0 1.259.259.934

4109.0 -198.0 1.201.201.954

4142.0 33.0 1.211.211 1.008

4111.0 -31.0 1.202.202.993

 

Показатели по 3-му признаку:

 

Признак Абсолютные Темпы Темпы Цепные темпы

N3 разности роста прироста роста

9073.0 ------ 1.000.000 -----

10219.0 1146.0 1.126.126 1.126

10407.0 188.0 1.147.147 1.018

10712.0 305.0 1.181.181 1.029

11421.0 709.0 1.259.259 1.066

12103.0 682.0 1.334.334 1.060

13719.0 1616.0 1.512.512 1.134

12402.0 -1317.0 1.367.367.904

10312.0 -2090.0 1.137.137.831

8611.0 -1701.0.949 -.051.835

7412.0 -1199.0.817 -.183.861

7206.0 -206.0.794 -.206.972

7914.0 708.0.872 -.128 1.098

8032.0 118.0.885 -.115 1.015

8171.0 139.0.901 -.099 1.017

8720.0 549.0.961 -.039 1.067

9023.0 303.0.994 -.006 1.035

9912.0 889.0 1.092.092 1.099

9987.0 75.0 1.101.101 1.008

10762.0 775.0 1.186.186 1.078

 

Показатели по 4-му признаку:

 

Признак Абсолютные Темпы Темпы Цепные темпы

N4 разности роста прироста роста

4466.0 ------ 1.000.000 -----

3945.0 -521.0.883 -.117.883

3849.0 -96.0.862 -.138.976

4480.0 631.0 1.003.003 1.164

4382.0 -98.0.981 -.019.978

4450.0 68.0.996 -.004 1.016

3212.0 -1238.0.719 -.281.722

5678.0 2466.0 1.271.271 1.768

7543.0 1865.0 1.689.689 1.328

8399.0 856.0 1.881.881 1.113

8956.0 557.0 2.005 1.005 1.066

9177.0 221.0 2.055 1.055 1.025

8204.0 -973.0 1.837.837.894

6956.0 -1248.0 1.558.558.848

7434.0 478.0 1.665.665 1.069

6300.0 -1134.0 1.411.411.847

6237.0 -63.0 1.397.397.990

5529.0 -708.0 1.238.238.886

5681.0 152.0 1.272.272 1.027

5742.0 61.0 1.286.286 1.011

 

Показатели по 5-му признаку:

 

Признак Абсолютные Темпы Темпы Цепные темпы

N5 разности роста прироста роста

2586.0 ------ 1.000.000 -----

2710.0 124.0 1.048.048 1.048

2943.0 233.0 1.138.138 1.086

2749.0 -194.0 1.063.063.934

2693.0 -56.0 1.041.041.980

2871.0 178.0 1.110.110 1.066

2312.0 -559.0.894 -.106.805

2877.0 565.0 1.113.113 1.244

2983.0 106.0 1.154.154 1.037

3217.0 234.0 1.244.244 1.078

3409.0 192.0 1.318.318 1.060

3126.0 -283.0 1.209.209.917

2971.0 -155.0 1.149.149.950

2763.0 -208.0 1.068.068.930

2697.0 -66.0 1.043.043.976

2903.0 206.0 1.123.123 1.076

2718.0 -185.0 1.051.051.936

2512.0 -206.0.971 -.029.924

2693.0 181.0 1.041.041 1.072

2914.0 221.0 1.127.127 1.082

 

 

Таблица абсолютных разностей

с указанием точек перегиба.

(единица под числом - перегиб,ноль - его отсутствие.)

 

--N------Y----------X1---------X2---------X3---------X4---

 

1. 86.0 302.0 1146.0 -521.0 124.0

1 1 1 1 1

2. 553.0 69.0 188.0 -96.0 233.0

0 1 1 1 1

3. 761.0 229.0 305.0 631.0 -194.0

1 0 1 1 1

4. 1680.0 295.0 709.0 -98.0 -56.0

1 1 0 1 1

5. 259.0 -209.0 682.0 68.0 178.0

0 1 1 1 1

6. 343.0 274.0 1616.0 -1238.0 -559.0

1 1 1 1 1

7. 1890.0 126.0 -1317.0 2466.0 565.0

1 0 1 0 1

8. 327.0 166.0 -2090.0 1865.0 106.0

1 1 0 1 1

9. -712.0 -181.0 -1701.0 856.0 234.0

1 1 0 1 0

10. -417.0 35.0 -1199.0 557.0 192.0

1 1 1 1 1

11. -195.0 86.0 -206.0 221.0 -283.0

1 1 1 1 1

12. -97.0 308.0 708.0 -973.0 -155.0

1 1 1 0 0

13. -1702.0 -304.0 118.0 -1248.0 -208.0

1 1 0 1 1

14. 411.0 -115.0 139.0 478.0 -66.0

1 1 1 1 1

15. -185.0 109.0 549.0 -1134.0 206.0

1 1 1 1 1

16. -463.0 -304.0 303.0 -63.0 -185.0

1 1 1 1 0

17. 241.0 -198.0 889.0 -708.0 -206.0

0 1 1 1 1

18. 269.0 33.0 75.0 152.0 181.0

0 1 1 1 0

19. 292.0 -31.0 775.0 61.0 221.0

 

 

Количество перегибов и их доля:

 

В 1-м столбце число перегибов равно: 14

Доля перегибов в этом столбце равна: 70.0%

Динамика пульсивна.

В 2-м столбце число перегибов равно: 16

Доля перегибов в этом столбце равна: 80.0%

Динамика пульсивна.

В 3-м столбце число перегибов равно: 14

Доля перегибов в этом столбце равна: 70.0%

Динамика пульсивна.

В 4-м столбце число перегибов равно: 16

Доля перегибов в этом столбце равна: 80.0%

Динамика пульсивна.

В 5-м столбце число перегибов равно: 14

Доля перегибов в этом столбце равна: 70.0%

Динамика пульсивна.

 

 

Количество совпадений и их доля:

 

Количество совпадений в 1-м и 2-м столбцах равно 12

Доля совпадений в этих столбцах равна: 85.7%

Количество совпадений в 1-м и 3-м столбцах равно 10

Доля совпадений в этих столбцах равна: 71.4%

Количество совпадений в 1-м и 4-м столбцах равно 12

Доля совпадений в этих столбцах равна: 85.7%

Количество совпадений в 1-м и 5-м столбцах равно 11

Доля совпадений в этих столбцах равна: 78.6%

 

 

Оценка жесткости динамической связи:

 

1-й признак-фактор имеет жесткую динамическую

связь с признаком-функцией.

2-й признак-фактор имеет жесткую динамическую

связь с признаком-функцией.

3-й признак-фактор имеет жесткую динамическую

связь с признаком-функцией.

4-й признак-фактор имеет жесткую динамическую

связь с признаком-функцией.

 

Определение направленности динамических рядов:

По крайним уровням ряда:

 

Направленность 1-го признака растущая.

Направленность 2-го признака растущая.

Направленность 3-го признака растущая.

Направленность 4-го признака растущая.

Направленность 5-го признака растущая.

 

По цепным темпам роста:

 

Средний цепной темп роста по 1-му признаку равен 1.0083

Динамика растущая.

Средний цепной темп роста по 2-му признаку равен 1.0097

Динамика растущая.

Средний цепной темп роста по 3-му признаку равен 1.0090

Динамика растущая.

Средний цепной темп роста по 4-му признаку равен 1.0133

Динамика растущая.

Средний цепной темп роста по 5-му признаку равен 1.0063

Динамика растущая.

 

 

Степень представительности генеральной

совокупности по годам:

 

1 ---------- 100.1%?

2 ---------- 105.0%?

3 ---------- 104.1%?

4 ---------- 104.9%?

5 ---------- 100.9%?

6 ---------- 102.9%?

7 ---------- 101.8%?

8 ---------- 101.4%?

9 ---------- 100.3%?

10 ---------- 100.0% +

11 ---------- 100.0%?

12 ---------- 100.1%?

13 ---------- 100.0% +

14 ---------- 100.3%?

15 ---------- 100.4%?

16 ---------- 100.0% +

17 ---------- 101.0%?

18 ---------- 98.9% +

19 ---------- 99.7% +

20 ---------- 102.9%?

 

Исходная информация некачественна,

либо связь между признаками не балансовая.

Признаки-факторы составляют:101.2%

 

Показатели вариации для 1-го признака:

 

Минимальное значение.195320E+05

Максимальное значение.254310E+05

Размах вариации.589900E+04

Среднее по признаку.227011E+05

Среднее линейное отклонение.123395E+04

Дисперсия.268529E+07

Ср-квадратическое отклонение.163868E+04

Козффициент вариации.543565E+01

Лин.коэффициент вариации.721854E+01

Коэффициент осцилляции.259856E+02

 

 

Показатели вариации для 2-го признака:

 

Минимальное значение.342100E+04

Максимальное значение.492100E+04

Размах вариации.150000E+04

Среднее по признаку.429465E+04

Среднее линейное отклонение.293120E+03

Дисперсия.128709E+06

Ср-квадратическое отклонение.358760E+03

Козффициент вариации.682524E+01

Лин.коэффициент вариации.835366E+01

Коэффициент осцилляции.349272E+02

 

 

Показатели вариации для 3-го признака:

 

Минимальное значение.720600E+04

Максимальное значение.137190E+05

Размах вариации.651300E+04

Среднее по признаку.980590E+04

Среднее линейное отклонение.140911E+04

Дисперсия.290754E+07

Ср-квадратическое отклонение.170515E+04

Козффициент вариации.143700E+02

Лин.коэффициент вариации.173890E+02

Коэффициент осцилляции.664192E+02

 

 

Показатели вариации для 4-го признака:

 

Минимальное значение.321200E+04

Максимальное значение.917700E+04

Размах вариации.596500E+04

Среднее по признаку.603100E+04

Среднее линейное отклонение.149270E+04

Дисперсия.308614E+07

Ср-квадратическое отклонение.175674E+04

Козффициент вариации.247505E+02

Лин.коэффициент вариации.291285E+02

Коэффициент осцилляции.989057E+02

 

 

Показатели вариации для 5-го признака:

 

Минимальное значение.231200E+04

Максимальное значение.340900E+04

Размах вариации.109700E+04

Среднее по признаку.283235E+04

Среднее линейное отклонение.189050E+03

Дисперсия.583527E+05

Ср-квадратическое отклонение.241563E+03

Козффициент вариации.667467E+01

Лин.коэффициент вариации.852872E+01

Коэффициент осцилляции.387311E+02

 

Расчет коэффициентов парной корреляции:

 

Промежуточные цифры для 1-й пары признаков:

Среднее по признаку-функции:.227011E+05

Среднее по признаку-фактору:.429465E+04

Среднее по их произведению:.979808E+08

Отклонение признака-функции:.163868E+04

Отклонение признака-фактора:.358760E+03

Коэффициент парной корреляции:.829547E+00

 

Промежуточные цифры для 2-й пары признаков:

Среднее по признаку-функции:.227011E+05

Среднее по признаку-фактору:.980590E+04

Среднее по их произведению:.222448E+09

Отклонение признака-функции:.163868E+04

Отклонение признака-фактора:.170515E+04

Коэффициент парной корреляции: -.560656E-01

 

Промежуточные цифры для 3-й пары признаков:

Среднее по признаку-функции:.227011E+05

Среднее по признаку-фактору:.603100E+04

Среднее по их произведению:.138799E+09

Отклонение признака-функции:.163868E+04

Отклонение признака-фактора:.175674E+04

Коэффициент парной корреляции:.656018E+00

 

Промежуточные цифры для 4-й пары признаков:

Среднее по признаку-функции:.227011E+05

Среднее по признаку-фактору:.283235E+04

Среднее по их произведению:.644888E+08

Отклонение признака-функции:.163868E+04

Отклонение признака-фактора:.241563E+03

Коэффициент парной корреляции:.483776E+00

 

Полученные коэффициенты парной корреляции:

.829547E+00

-.560656E-01

.656018E+00

.483776E+00

 

Коэффициенты регрессии:

---------------------------

| Kn | Значение |

---------------------------

| b1 |.227011E+05 |

---------------------------

 

Расчет абсолютной ошибки:

Итерация равна: 74

Абсолютная ошибка равна:.160095E+04

Относительная ошибка равна: 6.59%

Расчет произведен по 11-му уровню.

 

Ошибка не превышает регламента.

Имитация явления данным уравнением надежна.