
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Количественное измерение тесноты связи признака-функции и признаков-факторов методом парной корреляцииСодержание книги
Поиск на нашем сайте 3.1. Теоретическая справка о регрессии и корреляции Статистика разработала множество методов изучения связей, выбор которых зависит от целей исследования и от поставленных задач. Различают два типа связей между признаками: · функциональную (жестко детерминированную); · стохастическую. Строго определить различие этих типов связи можно тогда, когда они получают математическую формулировку. Функциональнойназывается связь, при которой с изменением значения одной из переменных вторая изменяется строго определенным образом, то есть значению факторного признака обязательно соответствует одно и только одно значение результативного признака. Стохастическойназывается связь, при которой с изменением значения одной из переменных вторая может в определенных пределах принимать любые значения с некоторыми вероятностями, но ее среднее значение изменяется по определенному закону. Корреляционная связь является частным случаем стохастической связи. Корреляция - соотношение между объективно существующими явлениями и процессами. Если случайные переменные причинно обусловлены, и можно в вероятностном смысле высказываться об их связи, то говорят, что имеет место корреляционная связь. Корреляционная связь - это связь, при которой определенному значению факторного признака соответствует лишь среднее значение результативного признака. Связь между двумя признаками (результативным и факторным или двумя факторными) называется парной корреляцией. Зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков называется частной корреляцией. Зависимость же результативного признака и двух или более факторных признаков, включенных в исследование, называется множественной корреляцией. Регрессия – это зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. При регрессионной связи одному и тому же значению признака-фактора могут соответствовать в зависимости от случая различные значения величины признака-функции. Регрессии различают: 1. Относительно числа явлений (переменных), учитываемых в регрессии: а) простую регрессию (она представляет собой регрессию между двумя переменными); б) множественную или частную регрессию (предполагается существование множества одновременно развивающихся, не зависимых друг от друга цепей причинно-следственных связей, среди которых часть может соответствовать прямой зависимости, а часть – обратной). 2. Относительно формы зависимости: а) линейную регрессию, выражаемую линейной функцией; б) нелинейную регрессию, выражаемую нелинейной функцией. 3. В зависимости от характера: а) положительную регрессию; б) отрицательную регрессию, которая ведет себя обратно положительной регрессии. Расчет корреляций и расчет регрессий - это два последовательных этапа одного и того же анализа данных. Они выполняются в аналитическом режиме. Корреляции используются для качественного анализа: отбора взаимосвязанных факторов и выделения той части выборки, на которой теснота связи максимальна. Затем для отобранных факторов и подвыборки проводится количественный анализ: строятся регрессионные функции взаимосвязи. Корреляционный анализ имеет своей задачей количественное определение тесноты связи между признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи). Теснота связи количественно выражается величиной коэффициентов корреляции. Регрессивный анализ заключается в определении аналитического выражения связи, в котором изменение результативного признака обуславливается влиянием одного или нескольких факторных признаков, а множество всех прочих факторов применяется за постоянные (или усредненные) величины. Корреляционно-регрессивный анализ включает в себя измерение тесноты и направления связи, а также установление аналитического выражения (формы) связи. При прямолинейной форме связи между признаком-функцией и признаком-фактором показатель тесноты связи двух признаков определяется по формуле линейного коэффициента корреляции r:
Индекс корреляции (форма корреляционного отношения), изменяющий криволинейную связь, определяется по формуле:
Коэффициент корреляции принимает значения в интервале:
|
||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 (24)
(24) - среднее по признаку-функции;
- среднее по признаку-функции; - среднее по признаку-фактору;
- среднее по признаку-фактору;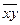 - среднее по произведению признака-фактора и признака-функции;
- среднее по произведению признака-фактора и признака-функции; - отклонение признака-фактора;
- отклонение признака-фактора; - среднее квадратическое отклонение признака-функции.
- среднее квадратическое отклонение признака-функции. (25)
(25) - общая дисперсия результативного признака, отображающая совокупное влияние всех признаков;
- общая дисперсия результативного признака, отображающая совокупное влияние всех признаков; - остаточная дисперсия, отображающая вариацию результативного признака от всех прочих, кроме факторов–признаков.
- остаточная дисперсия, отображающая вариацию результативного признака от всех прочих, кроме факторов–признаков. или по модулю от 0 до 1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости.
или по модулю от 0 до 1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости.


