
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Качественный анализ таблицы исходных динамических рядовСодержание книги
Поиск на нашем сайте
КУРСОВАЯ РАБОТА
По дисциплине: Статистика (наименование учебной дисциплины согласно учебному плану)
Тема: Системный анализ динамических рядов и построение уравнения многофакторной корреляционной связи
ВЫПОЛНИЛ: студент гр. ЭГР-09 ____________ / Птохова А.Б. / (подпись) (Ф.И.О.)
Оценка: _____________
Дата: ______________
ПРОВЕРИЛ:
Руководитель: профессор ____________ /Скобелина В. П./ (должность) (подпись) (Ф.И.О.)
Санкт-Петербург 2011 год
Кафедра экономики, учета и аудита Пояснительная записка
По дисциплине: Статистика (наименование учебной дисциплины согласно учебному плану)
ЗАДАНИЕ
Студенту группы ЭГР-09Птоховой А.Б. (шифр группы) (Ф.И.О.) 1. Тема проекта: Системный анализ динамических рядов и построение уравнения многофакторной корреляционной связи. 2. Содержание пояснительной записки: Курсовая работа включает решение комплексной статистической задачи построения уравнения множественной регрессии на конкретном информационном материале. 3. Перечень графического материала: В курсовой работе представлено 20 таблиц. 4. Срок сдачи законченного проекта: 15 декабря 2011 г. Руководитель проекта: профессор ____________ /Скобелина В.П./ (должность) (подпись) (Ф.И.О.)
Дата выдачи задания: 15 ноября 2011 г. Аннотация Данная курсовая работа нацелена на закрепление теоретических знаний, полученных в ходе изучения курса «Статистика». Работа включает решение комплексной статистической задачи построения уравнения множественной регрессии на конкретном информационном материале. Курсовая работа в своей теоретической части раскрывает такие понятия как динамические ряды и их характеристики, вариация, корреляция и регрессия. Работа включает качественный анализ исходных динамических рядов, расчёт показателей вариации и коэффициентов парной корреляции, а также построение уравнения многофакторной корреляционной связи.
Комплекс расчетных процедур выполняется по индивидуальным и стандартным программам на ПК. Объем курсовой работы 43 страницы. В качестве графического материала в работе представлено 20 таблиц. При написании курсовой работы было использовано 5 литературных источников. The summary This course work is targeted on fastening of theoretical knowledge, received in the process of studying the course «Statistics». Work includes the decision of complex statistical problem of building of equation of plural regression on specific information material. The theoretical part of the course work includes such concepts as dynamical rates and their characteristics, variation, correlation and regression. The work includes the qualitative analysis of initial dynamical rates, account of parameters of variation and factors of pair correlation, and also construction of the equation of multifactorial correlation communication. The whole complex of account procedures is executed with the help of individual and standard programms on РС. Volume of course work is 43 pages. As a graphic material in work 20 tables are presented. The course work was written with the help of 5 literary sources. Содержание
Введение. 4 1. Качественный анализ таблицы исходных динамических рядов. 5 1.1. Исходные данные. 5 1.2. Теоретическая справка о динамических рядах. 8 1.3. Анализ исходных динамических рядов на непрерывность. 12 1.4. Анализ характеристики динамики и её направленности. 15 1.5. Анализ характера связи между признаком-функцией и признаками-факторами. 18 2. Расчёт показателей вариации динамических рядов. 22 2.1. Теоретическая справка о показателях вариации динамических рядов. 22 2.2. Расчёт показателей вариации динамических рядов. 24 3. Количественное измерение тесноты связи признака-функции и признаков-факторов методом парной корреляции. 26 3.1. Теоретическая справка о регрессии и корреляции. 26 3.2. Расчёт коэффициентов парной корреляции. 28 4. Построение уравнений многофакторной корреляционной связи. 30 Заключение. 32 Список использованной литературы.. 33 Приложение 1. 34
Введение Статистика – комплекс учебных дисциплин, обеспечивающих овладение методологией статистического исследования массовых социально-экономических явлений и процессов с целью выявления закономерностей их развития в конкретных условиях места и времени. Большим шагом в развитии статистической науки стало применение компьютерной техники при анализе социально-экономических явлений. Данная курсовая работа нацелена на практическое закрепление знаний по базовым теоретическим дисциплинам учебной программы. Работа включает решение комплексной статистической задачи построения уравнения множественной регрессии на конкретном информационном материале. Выполнение работы сопряжено с использованием знаний, теоретических обобщений и навыков практического их применения по высшей и прикладной математике, общей теории статистики, а также теоретическим основам отраслевой экономики.
Работа над полученным заданием, представляющим собой индивидуальную таблицу исходных данных динамических рядов, включающих ряды признака–функции и признаков–факторов, содержит весь комплекс процедур, необходимых для полного системного анализа, который выполняется с помощью программы «Elvis» на персональном компьютере. Курсовая работа имеет комплексный характер, ее выполнение включает следующие стадии: 1. Проведение качественного анализа таблицы исходных данных динамических рядов. 2. Расчет показателей вариации динамических рядов. Ранжирование признаков-факторов. 3. Количественное измерение тесноты связи между динамикой признака-функции и определенного числа признаков-факторов методом парной корреляции. 4. Построение уравнения многофакторной корреляционной связи признака-функции с наиболее значимыми признаками-факторами. Каждая из перечисленных стадий решения общей задачи имеет свои методы и способы решения. Качественный анализ таблицы исходных динамических рядов Исходные данные Таблица исходных динамических рядов для выполнения курсовой работы включает динамические ряды признака-функции и четырёх признаков-факторов. В таблице 1 (в соответствии с вариантом задания 7.4) представлена информация о фактической стоимости геологоразведочных работ комплексной геологоразведочной экспедиции (КГРЭ), дифференцированной по видам полезных ископаемых (данные получены за 20 лет). Табл.1 Суммарная сметная стоимость геологоразведочных работ, дифференцированная по видам полезных ископаемых
Исходные динамические ряды сформированы из данных, полученных за 20 лет, при относительно постоянных внешних факторах для изучаемой совокупности (признака) за исследуемый период; стоимостные показатели представлены в сопоставимых ценах; геологоразведочные работы выполняются в одних и тех же территориальных границах; для КГРЭ характерна достаточно устойчивая производственно-технологическая структура. Данные, приведенные в таблице 1, выражены в одинаковом измерении (имеют место только абсолютные величины). В подлежащем таблицы исходного статистического материала находится динамический ряд обобщающего показателя (признака–функции) – суммарная сметная стоимость ГРР, величина которого в любом году изучаемого периода (уровень признака-функции) зависит в той или иной мере от уровня признаков-факторов, показанных в сказуемом таблицы. Признаки-факторы содержат информацию о сметной стоимости ГРР на чёрные металлы, цветные металлы, неметаллы (из них также на химическое сырьё).
Для того чтобы перейти к системному анализу динамических рядов, нужно проверить исходную информацию на качество и сопоставимость данных. Для этого необходимо выполнение следующего условия: сумма признаков-факторов по каждому уровню не должна превышать значение признака-функции на соответствующих уровнях. Воспользуемся формулами, характеризующими наличие полной балансовой связи в пределах изучаемой совокупности (1) и наличие представительной балансовой связи в пределах генеральной совокупности (2).
yt и xt – ежегодные уровни признака-функции и признака-фактора соответственно; x1, x2,…,xn – признаки-факторы; n – число признаков-факторов; Т – изучаемый период, в нашем случае Т = 20 лет.
i – индекс признака-фактора, i = 1,2,…,n; m – число изучаемых признаков-факторов, m<n Просуммируем значения признаков-факторов по каждому году. Они не должны превышать значений признака-функции, при этом не учитывается внутренняя сводка. Полученные данные отразим в таблице 2. Табл.2
Исходная информация качественна, различные уровни динамических рядов сопоставимы, сумма значений признаков-факторов не превышает 100%, следовательно, балансовая связь подтверждена. Таким образом, исходное информационное поле качественно, а значит, его данные можно использовать в программе «Elvis» для осуществления комплексного анализа динамических рядов. Программа требует наличия специального файла с данными, введенными в необходимом формате, а также выполнения всех запросов, возникающих при ее запуске. Запуск программы дает возможность получить результирующий файл, в котором исходные данные представлены в виде информационной матрицы (таблица 3).
Табл.3 Матрица информационного поля Исходные данные:
--N------Y----------X1---------X2---------X3---------X4---
1. 19532.0 3421.0 9073.0 4466.0 2586.0 2. 19618.0 3723.0 10219.0 3945.0 2710.0 3. 20171.0 3792.0 10407.0 3849.0 2943.0 4. 20932.0 4021.0 10712.0 4480.0 2749.0 5. 22612.0 4316.0 11421.0 4382.0 2693.0 6. 22871.0 4107.0 12103.0 4450.0 2871.0 7. 23214.0 4381.0 13719.0 3212.0 2312.0 8. 25104.0 4507.0 12402.0 5678.0 2877.0 9. 25431.0 4673.0 10312.0 7543.0 2983.0 10. 24719.0 4492.0 8611.0 8399.0 3217.0 11. 24302.0 4527.0 7412.0 8956.0 3409.0 12. 24107.0 4613.0 7206.0 9177.0 3126.0 13. 24010.0 4921.0 7914.0 8204.0 2971.0 14. 22308.0 4617.0 8032.0 6956.0 2763.0 15. 22719.0 4502.0 8171.0 7434.0 2697.0 16. 22534.0 4611.0 8720.0 6300.0 2903.0 17. 22071.0 4307.0 9023.0 6237.0 2718.0 18. 22312.0 4109.0 9912.0 5529.0 2512.0 19. 22581.0 4142.0 9987.0 5681.0 2693.0 20. 22873.0 4111.0 10762.0 5742.0 2914.0
В данной матрице символ N обозначает порядковый номер рассматриваемого уровня динамических рядов; Y - динамический ряд признака-функции (суммарная сметная стоимость ГРР); динамические ряды признаков-факторов обозначены как X1 (сметная стоимость ГРР на чёрные металлы), X2 (сметная стоимость ГРР на цветные металлы), X3 (сметная стоимость ГРР на неметаллы) и X4 (сметная стоимость ГРР на химическое сырьё). Поскольку данная матрица полностью соответствует качественному информационному полю, то это поле является одновременно операционным полем. Для выполнения комплексного анализа динамических рядов необходимо, чтобы операционное поле являлось также операционно-расчетным. Чтобы выяснить, существует ли в нашем случае подобное соответствие, следует более подробно остановиться на рассмотрении теоретических аспектов, связанных с понятием динамических рядов. 1.2. Теоретическая справка о динамических рядах Одно из основных положений научной методологии - необходимость изучать все явления в развитии, во времени. Это относится и к статистике: она должна дать характеристику изменений статистических показателей во времени. Специальная система статистических методов, предназначенная для изучения развития изменений во времени называется динамикой. Изучение динамики того или иного объекта, явления начинается с построения ряда динамики, или временного ряда. Динамический ряд или ряд динамики представляет собой ряд расположенных в хронологической последовательности числовых значений статистического показателя, который характеризует изменение общественных явлений во времени. В каждом ряду динамики имеются два основных элемента: время t и конкретное значение показателя (уровень ряда) y. В качестве показателей времени в рядах динамики выступают либо определённые даты (моменты) времени, либо отдельные периоды (годы, кварталы, месяцы, сутки). Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.
В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определённым датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на моментные и интервальные. Моментные ряды динамики отображают состояние изучаемых явлений на определённые даты (моменты) времени. Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Поэтому при суммировании уровней моментного ряда динамики может возникнуть повторный счет. Интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени. Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы времени. Свойство суммирования уровней за последовательные интервалы времени позволяет получать ряды динамики более укрупнённых периодов. Статистическое отображение развития изучаемого явления во времени может быть также представлено рядами динамики с нарастающими итогами. Их применение обусловлено потребностями отображения результатов развития изучаемых показателей не только за данный отчётный период, но и с учётом предшествующих периодов. При составлении таких рядов производится последовательное суммирование смежных уровней. Этим достигается суммарное обобщение результата развития изучаемого показателя с начала отчётного периода (месяца, квартала, года и т.д.). При построении динамических рядов необходимо соблюдать определённые правила: основным условием для получения правильных выводов при анализе рядов динамики и прогнозировании его уровней является сопоставимость уровней динамического ряда между собой. Статистические данные должны быть сопоставимы: · по территории - предполагает одни и те же границы территории; · кругу охватываемых объектов – сравнение совокупностей с равным числом элементов; · единицам измерения; · времени регистрации – обеспечивается равенством периодов времени, за которые приводятся данные; · ценам; · методологии расчета и проч. При изучении динамики общественных явлений возникает проблема описания интенсивности изменения и расчета средних показателей динамики. Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней, к таким показателям относятся: абсолютный прирост (разность между последующим уровнем и предыдущим), темпы роста (цепные и базисные, так как являются относительными величинами динамики), среднегодовой темп роста, базисные и цепные темпы прироста. Абсолютный прирост – разность между последующим и предыдущим (базисным или смежным) уровнями; подразделяется на базисный (3) и цепной (4) абсолютный прирост:
Абсолютный прирост позволяет выявить прерывность динамического ряда. Если колебания соседних абсолютных разностей превышают регламент, установленный содержанием признака, то ряд в этом месте разрывается. Абсолютные разности позволяют фиксировать точки перегиба ряда, когда знак абсолютной разности меняется на противоположный. Если абсолютная величина разностей соседних уровней не превышает для количественных признаков 30 %, а для качественных 15%, то ряд считается непрерывным. Доля точек перегиба в объеме ряда может характеризовать вид динамики. Если эта доля не более 5%, ряд характеризуется направленной динамикой. Если эта доля не более 30%, имеет место неустойчивая динамика ряда, а если доля превышает 30 %, то динамику называют вибрирующей. Темп роста – показатель интенсивности изменения уровня ряда, выраженный в процентах. Обозначив отдельные уровни динамического ряда последовательно и цепные: Темп прироста определяет относительную величину прироста. Аналогично темпы прироста, базисные и цепные, соответственно (7) и (8):
Цепные и базисные темпы роста взаимосвязаны, причем эта связь имеет двойное содержание: произведение цепных индексов динамического ряда равно отношению крайних уровней данного ряда (
Динамические ряды, составленные из темпов роста (прироста), могут быть цепными, базисными или смешанными. Общую направленность динамики можно определить по базисным темпам роста: если они больше единицы, динамика растущая, если меньше единицы, падающая. Но точное представление о направленности ряда дает среднегодовой темп роста, который позволяет также достаточно надежно оценить интенсивность динамики ряда в среднем за весь период:
Заключение В данной курсовой работе мы провели качественный анализ исходных динамических рядов. Выяснили, что динамическая связь между признаком-функцией и признаками-факторами жесткая, направленность динамики по всем признакам растущая, все признаки-факторы сонаправлены с признаком-функцией. Определение характера связи между признаком-функцией и признаками-факторами показало, что данная балансовая связь представительна. Для построения уравнения многофакторной корреляционной связи был осуществлен отбор из четырех признаков-факторов двух наиболее качественных. В итоге были составлены два уравнения множественной регрессии, которые являются корректными и надёжно имитируют динамику признака–функции, поскольку относительная ошибка в обоих случаях не превышает регламента. Таким образом, можно считать, что цель курсовой работы достигнута. Список использованной литературы 1. Гусаров В.М. – «Статистика: Учеб. Пособие для вузов» – М.: ЮНИТИ-ДАНА, 2003. – 463 с. 2. Елисеева И.И., Юзбашев М.М. – «Общая теория статистики» – М.: «Финансы и статистика», 2002 3. Харламов А.И. – «Общая теория статистики» - М., 1996. – 296 с. 4. Статистика: Учеб. Пособие для самостоятельной работы студентов/Сост.: В.П. Скобелина, Ю.В. Любек, Е.Г. Катышева. Санкт-Петербургский государственный горный институт (технический университет). СПб, 2005. 73 с. 5. Статистика: Методические указания к курсовой работе/Сост.: В.П. Скобелина, Ю.В. Любек, Е.Г. Катышева. Санкт-Петербургский государственный горный институт (технический университет). СПб, 2010. 16 с. Приложение 1 Распечатка результатов, полученных с помощью программы «Elvis», учитывающих наличие 4 признаков-факторов (Х1, Х2, Х3, Х4) и признака-функции (У) согласно варианту задания 1 (7.4).
ВАРИАНТ НОМЕР:74 Работу выполнил: Ptokhova Anna
Исходные данные:
--N------Y----------X1---------X2---------X3---------X4---
1. 19532.0 3421.0 9073.0 4466.0 2586.0 2. 19618.0 3723.0 10219.0 3945.0 2710.0 3. 20171.0 3792.0 10407.0 3849.0 2943.0 4. 20932.0 4021.0 10712.0 4480.0 2749.0 5. 22612.0 4316.0 11421.0 4382.0 2693.0 6. 22871.0 4107.0 12103.0 4450.0 2871.0 7. 23214.0 4381.0 13719.0 3212.0 2312.0 8. 25104.0 4507.0 12402.0 5678.0 2877.0 9. 25431.0 4673.0 10312.0 7543.0 2983.0 10. 24719.0 4492.0 8611.0 8399.0 3217.0 11. 24302.0 4527.0 7412.0 8956.0 3409.0 12. 24107.0 4613.0 7206.0 9177.0 3126.0 13. 24010.0 4921.0 7914.0 8204.0 2971.0 14. 22308.0 4617.0 8032.0 6956.0 2763.0 15. 22719.0 4502.0 8171.0 7434.0 2697.0 16. 22534.0 4611.0 8720.0 6300.0 2903.0 17. 22071.0 4307.0 9023.0 6237.0 2718.0 18. 22312.0 4109.0 9912.0 5529.0 2512.0 19. 22581.0 4142.0 9987.0 5681.0 2693.0 20. 22873.0 4111.0 10762.0 5742.0 2914.0
Исходные данные в абсолютных величинах:
--N------Y----------X1---------X2---------X3---------X4---
1. 19532.0 3421.0 9073.0 4466.0 2586.0 2. 19618.0 3723.0 10219.0 3945.0 2710.0 3. 20171.0 3792.0 10407.0 3849.0 2943.0 4. 20932.0 4021.0 10712.0 4480.0 2749.0 5. 22612.0 4316.0 11421.0 4382.0 2693.0 6. 22871.0 4107.0 12103.0 4450.0 2871.0 7. 23214.0 4381.0 13719.0 3212.0 2312.0 8. 25104.0 4507.0 12402.0 5678.0 2877.0 9. 25431.0 4673.0 10312.0 7543.0 2983.0 10. 24719.0 4492.0 8611.0 8399.0 3217.0 11. 24302.0 4527.0 7412.0 8956.0 3409.0 12. 24107.0 4613.0 7206.0 9177.0 3126.0 13. 24010.0 4921.0 7914.0 8204.0 2971.0 14. 22308.0 4617.0 8032.0 6956.0 2763.0 15. 22719.0 4502.0 8171.0 7434.0 2697.0 16. 22534.0 4611.0 8720.0 6300.0 2903.0 17. 22071.0 4307.0 9023.0 6237.0 2718.0 18. 22312.0 4109.0 9912.0 5529.0 2512.0 19. 22581.0 4142.0 9987.0 5681.0 2693.0 20. 22873.0 4111.0 10762.0 5742.0 2914.0
Одним из условий возможности проведения анализа динамических рядов является их непрерывность. В нашем случае ряды непрерывны.
За базу принят 1-й уровень.
Наличие в 3-ей,4-й и 5-й колонке значений <99.999> говорит о том,что имело место деление на ноль.
Показатели по 1-му признаку:
Признак Абсолютные Темпы Темпы Цепные темпы N1 разности роста прироста роста 19532.0 ------ 1.000.000 ----- 19618.0 86.0 1.004.004 1.004 20171.0 553.0 1.033.033 1.028 20932.0 761.0 1.072.072 1.038 22612.0 1680.0 1.158.158 1.080 22871.0 259.0 1.171.171 1.011 23214.0 343.0 1.189.189 1.015 25104.0 1890.0 1.285.285 1.081 25431.0 327.0 1.302.302 1.013 24719.0 -712.0 1.266.266.972 24302.0 -417.0 1.244.244.983 24107.0 -195.0 1.234.234.992 24010.0 -97.0 1.229.229.996 22308.0 -1702.0 1.142.142.929 22719.0 411.0 1.163.163 1.018 22534.0 -185.0 1.154.154.992 22071.0 -463.0 1.130.130.979 22312.0 241.0 1.142.142 1.011 22581.0 269.0 1.156.156 1.012 22873.0 292.0 1.171.171 1.013
Показатели по 2-му признаку:
Признак Абсолютные Темпы Темпы Цепные темпы N2 разности роста прироста роста 3421.0 ------ 1.000.000 ----- 3723.0 302.0 1.088.088 1.088 3792.0 69.0 1.108.108 1.019 4021.0 229.0 1.175.175 1.060 4316.0 295.0 1.262.262 1.073 4107.0 -209.0 1.201.201.952 4381.0 274.0 1.281.281 1.067 4507.0 126.0 1.317.317 1.029 4673.0 166.0 1.366.366 1.037 4492.0 -181.0 1.313.313.961 4527.0 35.0 1.323.323 1.008 4613.0 86.0 1.348.348 1.019 4921.0 308.0 1.438.438 1.067 4617.0 -304.0 1.350.350.938 4502.0 -115.0 1.316.316.975 4611.0 109.0 1.348.348 1.024 4307.0 -304.0 1.259.259.934 4109.0 -198.0 1.201.201.954 4142.0 33.0 1.211.211 1.008 4111.0 -31.0 1.202.202.993
Показатели по 3-му признаку:
Признак Абсолютные Темпы Темпы Цепные темпы N3 разности роста прироста роста 9073.0 ------ 1.000.000 ----- 10219.0 1146.0 1.126.126 1.126 10407.0 188.0 1.147.147 1.018 10712.0 305.0 1.181.181 1.029 11421.0 709.0 1.259.259 1.066 12103.0 682.0 1.334.334 1.060 13719.0 1616.0 1.512.512 1.134 12402.0 -1317.0 1.367.367.904 10312.0 -2090.0 1.137.137.831 8611.0 -1701.0.949 -.051.835 7412.0 -1199.0.817 -.183.861 7206.0 -206.0.794 -.206.972 7914.0 708.0.872 -.128 1.098 8032.0 118.0.885 -.115 1.015 8171.0 139.0.901 -.099 1.017 8720.0 549.0.961 -.039 1.067 9023.0 303.0.994 -.006 1.035 9912.0 889.0 1.092.092 1.099 9987.0 75.0 1.101.101 1.008 10762.0 775.0 1.186.186 1.078
Показатели по 4-му признаку:
Признак Абсолютные Темпы Темпы Цепные темпы N4 разности роста прироста роста 4466.0 ------ 1.000.000 ----- 3945.0 -521.0.883 -.117.883 3849.0 -96.0.862 -.138.976 4480.0 631.0 1.003.003 1.164 4382.0 -98.0.981 -.019.978 4450.0 68.0.996 -.004 1.016 3212.0 -1238.0.719 -.281.722 5678.0 2466.0 1.271.271 1.768 7543.0 1865.0 1.689.689 1.328 8399.0 856.0 1.881.881 1.113 8956.0 557.0 2.005 1.005 1.066 9177.0 221.0 2.055 1.055 1.025 8204.0 -973.0 1.837.837.894 6956.0 -1248.0 1.558.558.848 7434.0 478.0 1.665.665 1.069 6300.0 -1134.0 1.411.411.847 6237.0 -63.0 1.397.397.990 5529.0 -708.0 1.238.238.886 5681.0 152.0 1.272.272 1.027 5742.0 61.0 1.286.286 1.011
Показатели по 5-му признаку:
Признак Абсолютные Темпы Темпы Цепные темпы N5 разности роста прироста роста 2586.0 ------ 1.000.000 ----- 2710.0 124.0 1.048.048 1.048 2943.0 233.0 1.138.138 1.086 2749.0 -194.0 1.063.063.934 2693.0 -56.0 1.041.041.980 2871.0 178.0 1.110.110 1.066 2312.0 -559.0.894 -.106.805 2877.0 565.0 1.113.113 1.244 2983.0 106.0 1.154.154 1.037 3217.0 234.0 1.244.244 1.078 3409.0 192.0 1.318.318 1.060 3126.0 -283.0 1.209.209.917 2971.0 -155.0 1.149.149.950 2763.0 -208.0 1.068.068.930 2697.0 -66.0 1.043.043.976 2903.0 206.0 1.123.123 1.076 2718.0 -185.0 1.051.051.936 2512.0 -206.0.971 -.029.924 2693.0 181.0 1.041.041 1.072 2914.0 221.0 1.127.127 1.082
Таблица абсолютных разностей с указанием точек перегиба. (единица под числом - перегиб,ноль - его отсутствие.)
--N------Y----------X1---------X2---------X3---------X4---
1. 86.0 302.0 1146.0 -521.0 124.0 1 1 1 1 1 2. 553.0 69.0 188.0 -96.0 233.0 0 1 1 1 1 3. 761.0 229.0 305.0 631.0 -194.0 1 0 1 1 1 4. 1680.0 295.0 709.0 -98.0 -56.0 1 1 0 1 1 5. 259.0 -209.0 682.0 68.0 178.0 0 1 1 1 1 6. 343.0 274.0 1616.0 -1238.0 -559.0 1 1 1 1 1 7. 1890.0 126.0 -1317.0 2466.0 565.0 1 0 1 0 1 8. 327.0 166.0 -2090.0 1865.0 106.0 1 1 0 1 1 9. -712.0 -181.0 -1701.0 856.0 234.0 1 1 0 1 0 10. -417.0 35.0 -1199.0 557.0 192.0 1 1 1 1 1 11. -195.0 86.0 -206.0 221.0 -283.0 1 1 1 1 1 12. -97.0 308.0 708.0 -973.0 -155.0 1 1 1 0 0 13. -1702.0 -304.0 118.0 -1248.0 -208.0 1 1 0 1 1 14. 411.0 -115.0 139.0 478.0 -66.0 1 1 1 1 1 15. -185.0 109.0 549.0 -1134.0 206.0 1 1 1 1 1 16. -463.0 -304.0 303.0 -63.0 -185.0 1 1 1 1 0 17. 241.0 -198.0 889.0 -708.0 -206.0 0 1 1 1 1 18. 269.0 33.0 75.0 152.0 181.0 0 1 1 1 0 19. 292.0 -31.0 775.0 61.0 221.0
Количество перегибов и их доля:
В 1-м столбце число перегибов равно: 14 Доля перегибов в этом столбце равна: 70.0% Динамика пульсивна. В 2-м столбце число перегибов равно: 16 Доля перегибов в этом столбце равна: 80.0% Динамика пульсивна. В 3-м столбце число перегибов равно: 14 Доля перегибов в этом столбце равна: 70.0% Динамика пульсивна. В 4-м столбце число перегибов равно: 16 Доля перегибов в этом столбце равна: 80.0% Динамика пульсивна. В 5-м столбце число перегибов равно: 14 Доля перегибов в этом столбце равна: 70.0% Динамика пульсивна.
Количество совпадений и их доля:
Количество совпадений в 1-м и 2-м столбцах равно 12 Доля совпадений в этих столбцах равна: 85.7% Количество совпадений в 1-м и 3-м столбцах равно 10 Доля совпадений в этих столбцах равна: 71.4% Количество совпадений в 1-м и 4-м столбцах равно 12 Доля совпадений в этих столбцах равна: 85.7% Количество совпадений в 1-м и 5-м столбцах равно 11 Доля совпадений в этих столбцах равна: 78.6%
Оценка жесткости динамической связи:
1-й признак-фактор имеет жесткую динамическую связь с признаком-функцией. 2-й признак-фактор имеет жесткую динамическую связь с признаком-функцией. 3-й признак-фактор имеет жесткую динамическую связь с признаком-функцией. 4-й признак-фактор имеет жесткую динамическую связь с признаком-функцией.
Определение направленности динамических рядов: По крайним уровням ряда:
Направленность 1-го признака растущая. Направленность 2-го признака растущая. Направленность 3-го признака растущая. Направленность 4-го признака растущая. Направленность 5-го признака растущая.
По цепным темпам роста:
Средний цепной темп роста по 1-му признаку равен 1.0083 Динамика растущая. Средний цепной темп роста по 2-му признаку равен 1.0097 Динамика растущая. Средний цепной темп роста по 3-му признаку равен 1.0090 Динамика растущая. Средний цепной темп роста по 4-му признаку равен 1.0133 Динамика растущая. Средний цепной темп роста по 5-му признаку равен 1.0063 Динамика растущая.
Степень представительности генеральной совокупности по годам:
1 ---------- 100.1%? 2 ---------- 105.0%? 3 ---------- 104.1%? 4 ---------- 104.9%? 5 ---------- 100.9%? 6 ---------- 102.9%? 7 ---------- 101.8%? 8 ---------- 101.4%? 9 ---------- 100.3%? 10 ---------- 100.0% + 11 ---------- 100.0%? 12 ---------- 100.1%? 13 ---------- 100.0% + 14 ---------- 100.3%? 15 ---------- 100.4%? 16 ---------- 100.0% + 17 ---------- 101.0%? 18 ---------- 98.9% + 19 ---------- 99.7% + 20 ---------- 102.9%?
Исходная информация некачественна, либо связь между признаками не балансовая. Признаки-факторы составляют:101.2%
Показатели вариации для 1-го признака:
Минимальное значение.195320E+05 Максимальное значение.254310E+05 Размах вариации.589900E+04 Среднее по признаку.227011E+05 Среднее линейное отклонение.123395E+04 Дисперсия.268529E+07 Ср-квадратическое отклонение.163868E+04 Козффициент вариации.543565E+01 Лин.коэффициент вариации.721854E+01 Коэффициент осцилляции.259856E+02
Показатели вариации для 2-го признака:
Минимальное значение.342100E+04 Максимальное значение.492100E+04 Размах вариации.150000E+04 Среднее по признаку.429465E+04 Среднее линейное отклонение.293120E+03 Дисперсия.128709E+06 Ср-квадратическое отклонение.358760E+03 Козффициент вариации.682524E+01 Лин.коэффициент вариации.835366E+01 Коэффициент осцилляции.349272E+02
Показатели вариации для 3-го признака:
Минимальное значение.720600E+04 Максимальное значение.137190E+05 Размах вариации.651300E+04 Среднее по признаку.980590E+04 Среднее линейное отклонение.140911E+04 Дисперсия.290754E+07 Ср-квадратическое отклонение.170515E+04 Козффициент вариации.143700E+02 Лин.коэффициент вариации.173890E+02 Коэффициент осцилляции.664192E+02
Показатели вариации для 4-го признака:
Минимальное значение.321200E+04 Максимальное значение.917700E+04 Размах вариации.596500E+04 Среднее по признаку.603100E+04 Среднее линейное отклонение.149270E+04 Дисперсия.308614E+07 Ср-квадратическое отклонение.175674E+04 Козффициент вариации.247505E+02 Лин.коэффициент вариации.291285E+02 Коэффициент осцилляции.989057E+02
Показатели вариации для 5-го признака:
Минимальное значение.231200E+04 Максимальное значение.340900E+04 Размах вариации.109700E+04 Среднее по признаку.283235E+04 Среднее линейное отклонение.189050E+03 Дисперсия.583527E+05 Ср-квадратическое отклонение.241563E+03 Козффициент вариации.667467E+01 Лин.коэффициент вариации.852872E+01 Коэффициент осцилляции.387311E+02
Расчет коэффициентов парной корреляции:
Промежуточные цифры для 1-й пары признаков: Среднее по признаку-функции:.227011E+05 Среднее по признаку-фактору:.429465E+04 Среднее по их произведению:.979808E+08 Отклонение признака-функции:.163868E+04 Отклонение признака-фактора:.358760E+03 Коэффициент парной корреляции:.829547E+00
Промежуточные цифры для 2-й пары признаков: Среднее по признаку-функции:.227011E+05 Среднее по признаку-фактору:.980590E+04 Среднее по их произведению:.222448E+09 Отклонение признака-функции:.163868E+04 Отклонение признака-фактора:.170515E+04 Коэффициент парной корреляции: -.560656E-01
Промежуточные цифры для 3-й пары признаков: Среднее по признаку-функции:.227011E+05 Среднее по признаку-фактору:.603100E+04 Среднее по их произведению:.138799E+09 Отклонение признака-функции:.163868E+04 Отклонение признака-фактора:.175674E+04 Коэффициент парной корреляции:.656018E+00
Промежуточные цифры для 4-й пары признаков: Среднее по признаку-функции:.227011E+05 Среднее по признаку-фактору:.283235E+04 Среднее по их произведению:.644888E+08 Отклонение признака-функции:.163868E+04 Отклонение признака-фактора:.241563E+03 Коэффициент парной корреляции:.483776E+00
Полученные коэффициенты парной корреляции: .829547E+00 -.560656E-01 .656018E+00 .483776E+00
Коэффициенты регрессии: --------------------------- | Kn | Значение | --------------------------- | b1 |.227011E+05 | ---------------------------
Расчет абсолютной ошибки: Итерация равна: 74 Абсолютная ошибка равна:.160095E+04 Относительная ошибка равна: 6.59% Расчет произведен по 11-му уровню.
Ошибка не превышает регламента. Имитация явления данным уравнением надежна.
КУРСОВАЯ РАБОТА
По дисциплине: Статистика (наименование учебной дисциплины согласно учебному плану)
Тема: Системный анализ динамических рядов и построение уравнения многофакторной корреляционной связи
ВЫПОЛНИЛ: студент гр. ЭГР-09 ____________ / Птохова А.Б. / (подпись) (Ф.И.О.)
Оценка: _____________
Дата: ______________
ПРОВЕРИЛ:
Руководитель: профессор ____________ /Скобелина В. П./ (должность) (подпись) (Ф.И.О.)
Санкт-Петербург 2011 год
|

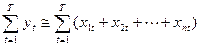 (1)
(1) (2)
(2) (3)
(3)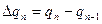 (4)
(4) получим темпы роста, базисные:
получим темпы роста, базисные: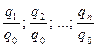 (5)
(5)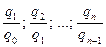 (6)
(6) (7)
(7) (8)
(8) ); при делении последующего базисного темпа на предыдущий получается цепной темп последующего периода:
); при делении последующего базисного темпа на предыдущий получается цепной темп последующего периода: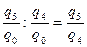 (9)
(9) (10)
(10) - цепные (или базисные) темпы роста.
- цепные (или базисные) темпы роста.


