
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайной называется переменная величина, которая в резуль-тате опыта принимает то или иное значение, заранее неизвестно, ка-кое именно.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Случайные величины принято обозначать заглавными латинскими буквами: X, Y, Z,..., а их возможные значения - соответствующими строчными буквами: x, y, z,... Различают два типа случайных величин: дискретные и непрерывные. Случайная величина называется дискретной, если её возможные значения образуют последовательность отдельных, изолированных друг от друга значений, которые можно перечислить, и непрерывной, если её возможные значения непрерывно заполняют некоторый интервал. Примеры случайных величин: - дискретных: число попаданий или промахов в серии выстрелов, число выпадений герба или решки при подбрасывании монеты, в схеме Бернулли повторяющихся независимых испытаний - число появлений со-бытия при n испытаниях и т.п.; - непрерывных: отклонение размера детали от номинального, ресурс (время безотказной работы) системы, физические параметры системы (температура, давление, влажность), длина тормозного пути автомобиля, продолжительность жизни человека и т.п. Закон распределения случайной величины Случайная величина полностью определена с вероятностной точки зрения, если известен ее закон распределения. Законом распределения случайной величины называется соотно-шение между возможными значениями этой величины и соответ-ствующими им вероятностями. Закон распределения может быть задан таблично, графически или аналитически. Простейшей формой задания закона распределения дискретной слу-чайной величины является таблица, состоящая из двух строк, в первой из которых перечислены возможные значения случайной величины X, а второй - соответствующие им вероятности.
Такая таблица называется рядом распределения, а ее графическое изображение - многоугольником распределения. Заметим, что сумма вероятностей всех возможных значений случай-ной величины должна быть равна единице:
Ряд распределения может быть построен только для дискретных слу-чайных величин. Пример. В партии, содержащей 12 изделий, имеются 3 бракованных. Выбраны случайным образом 4 изделия для проверки их качества. Найти закон распределения случайной величины X - числа бракованных изделий среди отобранных. Решение. Число бракованных изделий среди отобранных - это заранее неизвестная дискретная случайная величина, возможные значения которой
Здесь N =12, m =4, n =3, поэтому
В результате получим
Пример. Автомобиль должен проехать по улице, на которой уста-новлены 3 светофора, дающие независимо друг от друга зеленый сигнал в течение 30 сек., желтый - в течение 5 сек., красный – в течение 25 сек. По-строить закон распределения числа остановок автомобиля. Решение. Число остановок автомобиля X - дискретная случайная величина, возможные значения которой
следовательно, вероятность проезда q = 1 - p = 0,5. Проезд автомобиля мимо каждого светофора можно рассматривать как от-дельное независимое испытание. По формуле Бернулли находим
Поэтому ряд распределения числа остановок автомобиля будет иметь вид
Функциональные характеристики Случайной величины Для аналитического описания закона распределения случайной вели-чины применяют интегральную функцию распределения вероятностей или дифференциальную функцию распределения вероятностей случайной величины (её также называют плотностью распределения вероятностей или плотностью вероятностей). Интегральная функция распределения Вероятностей случайной величины Интегральной функцией распределения вероятностей случайной ве-личины F(x)называется вероятность того, что в результате опыта случай-ная величина X примет значение, меньшее произвольно заданного числа x, то есть
Свойства F(x). 1. 2.
3. Если возможные значения 4. 5. Вероятность попадания случайной величины X на конечный интервал [ a,b) равна приращению интегральной функции на этом интервале
6. В пределе, при стягивании интервала в точку
Следовательно, если X - непрерывная случайная величина, то F(x) -непрерывная функция, и вероятность того, что X примет одно определен-ное значение (то есть вероятность попадания X в точку a),равна нулю. Поэтому для непрерывной случайной величины X справедливы равенства
Если F(x) разрывна в точке a, то скачок функции F(x) в этой точке равен вероятности попадания X в неё. Поэтому для дискретных случайных величин
где суммирование распространяется на все те значения Пример. Ряд распределения дискретной случайной величины имеет вид
Найти интегральную функцию распределения и построить ее график. Решение. По теореме сложения вероятностей для несовместных со-бытий найдем: Для при при Если Следовательно, искомая функция распределения имеет вид
Пример. Случайная величина Х задана интегральной функцией рас-пределения
Найти вероятность того, что в результате трех независимых испы-таний величина Х дважды примет значение, принадлежащее интервалу (0,25; 0,75). Решение. Вероятность попадания Х на интервал (0,25; 0,75) в од-ном испытании равна
По формуле Бернулли Плотность вероятностей Пусть X – непрерывная случайная величина с функцией распреде-ления F(x), которую будем предполагать не только непрерывной, но и диф-ференцируемой. Вероятность попадания X на малый интервал
Отношение этой вероятности к длине участка
Функция В отличие от F(x) плотность вероятностей не является универсальной характеристикой распределения, а существует только для непрерывных случайных величин. Вероятность попадания непрерывной случайной величины на конеч-ный интервал
Полагая в этой формуле
то есть определение интегральной функции распределения Свойства f(x). 1. 2. Условие нормировки 3. Если все возможные значения Пример. Непрерывная случайная величина X задана плотностью вероятностей:
Найти: параметр Решение. По условию нормировки
При При При Итак,
3). Пример. Плотность вероятностей задана графически с точностью до неизвестного параметра b (см. рис.). Найти: полное аналитическое выражение для f(x); F(x);
Решение. 1). Так как площадь под кривой распределения по условию нормировки равна единице, то
2). Интегральная функция распределения будет равна: при при при
при
Итак,
3). Замечание. Так как для непрерывной случайной величины F(x) - непрерывная функция, то ее значения не должны претерпевать разрывов на границах интервалов изменения x. Это должно служить контролем пра-вильности вычислений F(x).
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 867; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.141.201 (0.01 с.) |



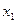


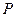
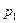




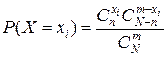 .
.





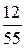

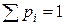
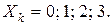 Вероятность оста-новки перед каждым светофором
Вероятность оста-новки перед каждым светофором ,
, (k = 0, 1, 2, 3).
(k = 0, 1, 2, 3).
 - универсальная характеристика, существующая и для дискретных и для непрерывных случайных величин.
- универсальная характеристика, существующая и для дискретных и для непрерывных случайных величин. так как F(x) – вероятность.
так как F(x) – вероятность. так как
так как  - невозможное событие.
- невозможное событие. так как
так как 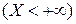 - достоверное событие.
- достоверное событие. то
то 
 - неубывающая функция, то есть
- неубывающая функция, то есть  , если
, если  .
.



 , которые мень-ше x, и график функции распределения дискретной случайной величины представляет собой ступенчатую функцию, непрерывную слева.
, которые мень-ше x, и график функции распределения дискретной случайной величины представляет собой ступенчатую функцию, непрерывную слева.
 , так как значения
, так как значения  случайная ве-личина Х не принимает;
случайная ве-личина Х не принимает;
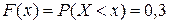 , так как Х может принять зна-чение 1 с вероятностью 0,3;
, так как Х может принять зна-чение 1 с вероятностью 0,3;
 .
.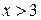 , то
, то  , так как событие
, так как событие  достоверно, и его вероятность равна единице.
достоверно, и его вероятность равна единице.
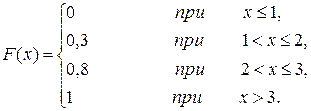

 .
.
 равна
равна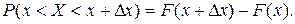
 обозначают через f(x):
обозначают через f(x):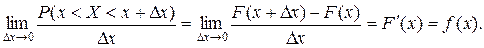
 - первая производная от интегральной функ-ции распределения
- первая производная от интегральной функ-ции распределения  равна определенному интегралу от плотности веро-ятностей, взятому в пределах от
равна определенному интегралу от плотности веро-ятностей, взятому в пределах от 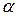 до
до  :
: .
. и учитывая определение F(x), получим
и учитывая определение F(x), получим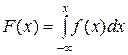 ,
, , то есть f(x) - неотрицательная функция.
, то есть f(x) - неотрицательная функция.
 Следовательно, пло-щадь, ограниченная графиком плотности вероятностей и осью
Следовательно, пло-щадь, ограниченная графиком плотности вероятностей и осью 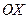 , равна единице.
, равна единице. то
то 

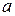 ; интегральную функцию распределения F(x); вероятность попадания X на интервал
; интегральную функцию распределения F(x); вероятность попадания X на интервал  .
.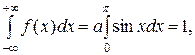 отсюда
отсюда
 , поэтому
, поэтому 

 .
.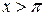





 откуда
откуда  Поэтому
Поэтому




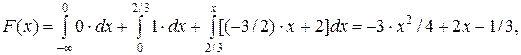
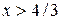


 .
.


