
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическое распределениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть производится ряд независимых испытаний (”попыток”) для достижения некоторого результата (события
где Вероятности Ряд распределения
Математическое ожидание и дисперсия
Пример. Производится ряд попыток включить двигатель. Каждая занимает время Решение. Число попыток
По свойствам математического ожидания и дисперсии
Пример. Имеется Решение. По условию
3.4. Гипергеометрическое распределение Пусть в урне N шаров, из них n белых, остальные черные. Случайно отбирают m шаров, причем отобранный шар перед отбором следующего не возвращается обратно (поэтому формула Бернулли неприменима). Пусть Как известно, вероятность того, что из m отобранных шаров ровно k белых равна
Эта формула определяет распределение случайной величины k, называемое гипергеометрическим. Оно характеризуется тремя параметрами: N, m, n. Пример построения гипергеометрического закона распределения приведен на стр. 40. Закон равномерного распределения вероятностей Непрерывная случайная величина Х подчинена закону равномерного распределения вероятностей, если на интервале, которому принадлежат все возможные значения Х, плотность вероятностей постоянна и равна
Графики плотности вероятностей равномерно распределенной слу-чайной величины Х и функции распределения F(x) показаны на рисунке.
Обычно вместо параметров a и b используют математическое ожи-дание Х и половину ширины Очевидно, Дисперсия закона равномерного распределения Вероятность попадания равномерно распределенной случайной величины на интервал
Пример. Поезда метрополитена идут с интервалом 2 мин. Пассажир выходит на платформу в некоторый момент времени. Найти среднее зна-чение времениожидания поезда, его дисперсию и вероятность того, что пассажир будет ожидать очередной поезд не более 0,5 мин. Решение. Пусть Т - время ожидания поезда. Это непрерывная слу-чайная величина, равномерно распределенная в интервале (0,2). Следова-тельно,
Пример. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти ве-роятность того, что при отсчете будет сделана ошибка, превышающая 0,05. Решение. Ошибку округления можно рассматривать как непре-рывную случайную величину X, распределеннуюравномерно в интервале между двумя соседними делениями. В рассматриваемой задаче длина ин-тервала Ошибка округления превышает 0,05, если она заключена в интервале
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 606; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.160.6 (0.01 с.) |

 ), и при каждой попытке событие
), и при каждой попытке событие  . Тогда число попыток
. Тогда число попыток 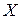 до появления события
до появления события  …. Вероятности их по теореме умножения вероятностей для независимых событий равны
…. Вероятности их по теореме умножения вероятностей для независимых событий равны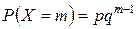


 .
. образуют для ряда последовательных значений
образуют для ряда последовательных значений  (поэтому распределение называется гео-метрическим).
(поэтому распределение называется гео-метрическим). имеет вид
имеет вид



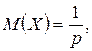
 .
.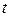 и заканчивается успешно независимо от других с веро-ятностью
и заканчивается успешно независимо от других с веро-ятностью  , которое потребуется для включения двигателя, найти его математическое ожида-ние и дисперсию.
, которое потребуется для включения двигателя, найти его математическое ожида-ние и дисперсию. Поэтому общее время
Поэтому общее время  - тоже случайная величина, подчиненная геометрическому закону распределения, и ее ряд распределения будет иметь вид
- тоже случайная величина, подчиненная геометрическому закону распределения, и ее ряд распределения будет иметь вид

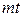
 ,
,  .
. лампочек; каждая из них с вероятностью
лампочек; каждая из них с вероятностью  имеет дефект. Лампочка ввинчивается в патрон и включается ток; при этом дефектная лампочка сразу же перегорает и заменяется новой. Построить ряд распределения числа лампочек
имеет дефект. Лампочка ввинчивается в патрон и включается ток; при этом дефектная лампочка сразу же перегорает и заменяется новой. Построить ряд распределения числа лампочек 
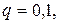
 Ряд распределения
Ряд распределения 

 .
. - число белых шаров среди отобранных. Очевидно, это дискретная случайная величина. Ее возможные значения:
- число белых шаров среди отобранных. Очевидно, это дискретная случайная величина. Ее возможные значения: 



 области возможных значений случайной величины.
области возможных значений случайной величины.


 , принадлежащий
, принадлежащий  , равна
, равна .
.
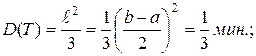

 в котором заключены возможные значения X, равна 0,2. Поэтому плотность равномерного распределения вероятностей
в котором заключены возможные значения X, равна 0,2. Поэтому плотность равномерного распределения вероятностей  вне этого интервала
вне этого интервала 
 Так как
Так как  то
то



