
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрические, газодинамические и режимные характеристики турбинных решетокСодержание книги
Поиск на нашем сайте
ВВЕДЕНИЕ Паровая турбина – это тепловой двигатель, в котором потенциальная энергия пара последовательно превращается в кинетическую энергию потока, истекающего из сопел, а из кинетической – в механическую энергию вращения ротора на рабочих лопатках. Основными преимуществами паровых турбин являются компактность, быстроходность, высокая единичная мощность, высокий КПД. Паровая турбина является основным двигателем тепловых и атомных электростанций. Помимо выработки электроэнергии, в паротурбинных установках возможно реализовать комбинированное производство тепловой и электрической энергии (на ТЭЦ), что очень существенно повышает эффективность использования топлива. Рассмотрим типовую конструкцию паровой одноцилиндровой конденсационной турбины К–50–90 мощностью 50 МВт c начальными параметрами пара 8,8 МПа (88 бар) и 535 оС, рис.1. Турбина имеет сопловое парораспределение, особенностью которого является последовательное (а не одновременное) прикрытие четырех регулирующих клапанов при необходимости снижения мощности турбины. От каждого регулирующего клапана пар подводится к своей сопловой коробке. Ротор турбины – комбинированного типа. Первые 19 дисков, расположенные в зоне высоких температур, откованы заодно с валом (цельнокованая часть), последние три насажены на вал с натягом (насадная часть). Проточная часть турбины состоит из 22 ступеней. Первая ступень турбин с сопловым парораспределением называется регулирующей, далее идут нерегулируемые ступени. Проточная часть ступени состоит из неподвижной сопловой решетки, закрепленной в диафрагме или в сопловой коробке и вращающейся рабочей решетки, закрепленной на диске. В сопловой решетке происходит мощное ускорение потока пара за счет понижения давления. В рабочей решетке происходит преобразование кинетической энергии этого потока в энергию вращения ротора. Ротор турбины вращает ротор электрического генератора. По мере понижения давления пара от ступени к ступени его удельный объем увеличивается, что заставляет увеличивать высоту лопаток. На переднем конце ротора установлен главный масляный насос, регулятор скорости и бойки автомата безопасности. Главный масляный насос служит для подачи масла к подшипникам турбины и генератора (1,5 бар), и в систему автоматического регулирования (20 бар). Регулятор скорости в составе системы автоматического регулирования поддерживает строго постоянное число оборотов ротора турбины (в этой и почти всех турбинах ТЭС – 3000 об/мин, в турбинах АЭС–3000 и 1500 об/мин). Автомат безопасности обеспечивает аварийное закрытие стопорных и регулирующих клапанов турбины и ее останов при недопустимом повышении числа оборотов (свыше 10–12 % по сравнению с номинальным). Задний конец ротора соединен полугибкой муфтой с ротором генератора. Статор турбины включает в себя корпус, сопловые коробки регулирующей ступени, клапанные коробки регулирующих клапанов, обоймы диафрагм, сами диафрагмы, обоймы концевых уплотнений. Передняя часть корпуса в зоне высоких давлений – литая, толстостенная; средняя и выхлопная часть, в зоне низких давлений – сварная, тонкостенная. Картер переднего подшипника служит для размещения опорно– упорного подшипника, систем защиты и автоматического регулирования, элементов системы маслоснабжения. Картер заднего подшипника служит для размещения опорных подшипников турбины и генератора, соединительной муфты и валоповоротного устройства. Передний картер может свободно перемещаться вдоль фундаментной плиты по направляющим шпонкам при тепловых расширениях корпуса. Задний картер встроен в выхлопной патрубок турбины и вместе с ним остается неподвижным. Здесь расположена «мертвая точка» или «фикс–пункт» турбины, от которой тепловые расширения корпуса организованы в сторону переднего картера. Валоповоротное устройство служит для медленного проворачивания ротора при пуске и останове турбины. Это предотвращает тепловые искривления ротора от неравномерного прогрева и остывания. Система автоматического регулирования включает четыре регулирующих клапана, распределительный кулачковый валик, сервомотор, золотник, регулятор скорости и др. Импульс по изменению числа оборотов поступает от регулятора скорости к золотнику, а от него – к сервомотору. Сервомотор поворачивает кулачковый валик и открывает или закрывает регулирующие клапаны последовательно один за другим. Благодаря последовательному прикрытию регулирующих клапанов при сопловом парораспределении снижаются потери давления от дросселирования свежего пара перед турбиной. Это объясняется тем, что дросселированию подвергается не весь расход пара, а только та его часть, которая проходит через частично открытый клапан, представляющий высокое сопротивление потоку. В нижней половине корпуса вварены патрубки для организации отборов пара на регенеративный подогрев питательной воды. Регенеративный подогрев снижает потери тепла в конденсаторе турбины и заметно повышает ее абсолютный КПД.
ГЕОМЕТРИЧЕСКИЕ, ГАЗОДИНАМИЧЕСКИЕ И РЕЖИМНЫЕ ХАРАКТЕРИСТИКИ ТУРБИННЫХ РЕШЕТОК
Общие сведения
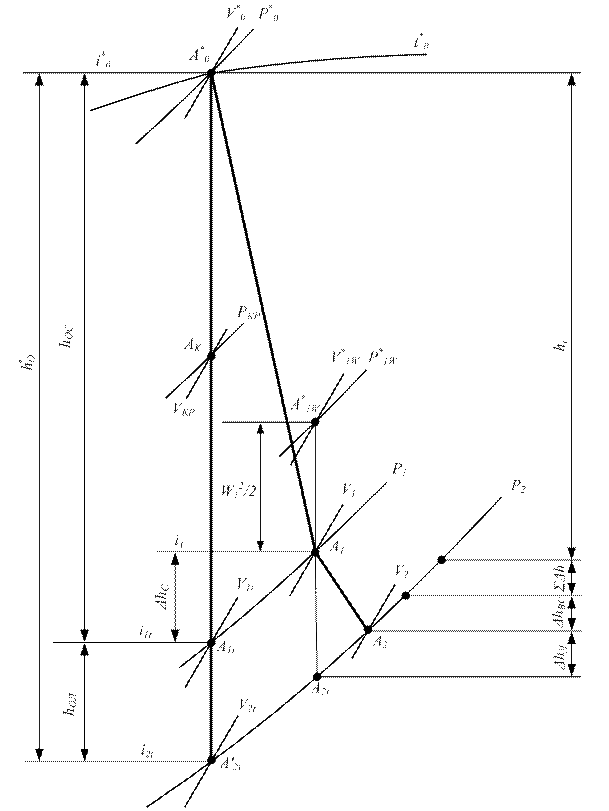
Преобразование энергии в турбинной ступени происходит в результате взаимодействия потока с неподвижными сопловыми и вращающимися рабочими лопатками, образующими сопловую и рабочую решетку. Протекая через межлопаточные каналы, поток изменяет скорость и направление движения. В сопловых каналах поток разгоняется до высокой скорости. Здесь потенциальная энергия пара (перепад энтальпий h0с) преобразуется в кинетическую. Струя газа, выходящая с большой скоростью из сопел, обтекает рабочую решетку. Здесь кинетическая энергия потока преобразуется в механическую энергию вращения рабочей решетки вместе с рабочим колесом. Параметры потока перед ступенью (сопловой решеткой) обозначаются индексом «0», за сопловой решеткой – индексом «1», за рабочей решеткой – индексом «2», рис.2. С0 и α0– абсолютная скорость и угол входа потока в сопловую решетку. Абсолютная скорость потока на выходе из сопловой решетки – С1, угол выхода потока – α1. Поскольку рабочие лопатки вращаются с окружной скоростью U, поток входит в рабочую решетку с относительной скоростью W1, под углом β1. Из вращающейся рабочей решетки поток выходит с относительной скоростью W2 под углом β2. Скорость C2 и угол α2 – абсолютная скорость и угол выхода из ступени (для следующей ступени – это скорость и угол входа в сопловую решетку С0 и α0). Особенности течения пара в турбинной решетке, т.е. газодинамические характеристики, определяются в зависимости от геометрических и режимных характеристик.
Геометрические характеристики: b1, b2 – хорда соплового и рабочего профиля соответственно; B1, B2 – ширина решеток; t1, t2 – шаг решеток; l1, l2 – высота лопаток; dк – корневой диаметр ступени; dср – средний диаметр; dп – периферийный диаметр; ∆1, ∆2 – толщина выходной кромки; О1, О2 – ширина выходного сечения соплового и рабочего каналов соответственно;
Параметры, определяющие форму межлопаточного канала, принято выражать в безразмерных относительных величинах, называемых относительными геометрическими характеристиками:
Если угол натекания потока на рабочие лопатки Когда сопловые каналы занимают только часть окружности ступени, такой подвод газа называется парциальным. Степень парциальности – это отношение дуги, занятой соплами, к длине окружности ступени:
Здесь Важными геометрическими характеристиками решеток являются углы поворота межлопаточных каналов:
а также площади выходного сечения:
Формы профилей лопаток и межлопаточных каналов в первую очередь определяются углами поворота По назначению решетки делятся на два типа: 1) реактивные сопловые и рабочие; 2) активные рабочие и поворотные. В пределах каждого типа решетки разделяются на несколько групп в зависимости от числа Маха [1]: – – – –
Режимные характеристики 1. Скорость потока на выходе из решетки: С1 и W2. 2. Степень расширения в решетке:
где 3. Число Маха:
где 4. Число Рейнольдса, характеризующее влияние сил вязкости:
где 5. Угол входа потока в решетку 6. Характеристическое число, определяющее уровень экономичности ступени:
где
Оборудование. Исходные данные
Работа выполняется на последней ступени паровой турбины для привода питательного насоса ОВПТ–270А. Параметры пара перед ступенью: давление за ступенью: частота вращения ротора: степень реактивности: Значения параметров задаются в диапазоне: Порядок выполнения работы 1. Снять отпечатки профилей сопловой и рабочей решеток. Измерениями на турбине определить средний диаметр dср, высоту сопловых и рабочих лопаток l1, l2, число сопловых лопаток z1. Измерениями на отпечатках определить остальные геометрические характеристики (рис.1, табл. 1 Приложения). 2. Вычертить профили в масштабе 2:1 и обозначить на чертеже их геометрические характеристики. 3. Построить теоретический процесс расширения пара в ступени на диаграмме H-S. Определить недостающие параметры. 4. Определить режимные и газодинамические характеристики (табл.2 Приложения). 5. Составить отчет по работе, в котором привести исходные данные, чертежи профилей с обозначениями геометрических характеристик, результаты измерений и расчетов в форме таблиц 1 и 2 Приложения. Содержание отчета Отчет должен содержать: 1) исходные данные; 2) геометрические, газодинамические и режимные характеристики в форме таблиц 1 и 2 Приложения; 3) чертежи профилей в масштабе аналогично рис.1; 4) процесс расширения пара в координатах H-S.
Контрольные вопросы
1. Дать определения геометрических характеристик решеток. 2. Дать определения газодинамических характеристик. 3. Дать определения режимных характеристик. 4. Дать определения относительных геометрических характеристик. 5. Расшифровать обозначения профилей С–90–12А и Р–35–25Б. 6. Дать определения и привести формулы для действительных и теоретических скоростей выхода из решеток С1, С1t, W2, W2t. 7. Сформулировать понятия угла атаки, безударного натекания. 8. Сформулировать понятия положительных и отрицательных углов атаки (прокомментировать по чертежу). 9. Дать определения лопаточных углов. 10. Сформулировать определения чисел Маха и Рейнольдса для сопловой и рабочей решеток. 11. Прокомментировать процесс расширения пара в ступени. 12. Изложить принцип действия турбины, ее устройство, назначение основных элементов (ротор, диски, лопатки, диафрагмы, подшипники опорные и упорные, корпус, уплотнения диафрагм, концевые уплотнения, регулирующие клапаны, валоповоротное устройство, муфта).
Лабораторная работа № 2 Общие сведения Утечка пара из корпуса турбины, а также перетечки в ступенях через зазоры между диафрагмой и ротором, рабочими лопатками и корпусом приводят к снижению КПД. Для уменьшения утечек широко используются бесконтактные лабиринтовые уплотнения (рис. 3). Уплотнения состоят из тонких гребней, установленных в ряд, с минимальными зазорами между вращающимися и неподвижными деталями. Между гребнями образуются расширительные камеры. Перепад давлений на уплотнение распределяется между всеми зазорами, поэтому на каждый зазор приходится относительно невысокий перепад. В каждом зазоре за счет понижения давления и энтальпии (например, процесс А-А1) пар разгоняется (рис.4). В каждой расширительной камере скорость гасится, кинетическая энергия переходит в тепловую и энтальпия восстанавливается на начальном уровне i0 (процесс А1 – В). В следующем зазоре поток снова ускоряется и снова его скорость гасится в расширительной камере. Этот процесс повторяется от зазора к зазору. Давление пара при движении вдоль уплотнения постепенно падает, удельный объём возрастает. Уравнение неразрывности для уплотнения:
где Расход через уплотнение определяется расходом через первый зазор. Так как суммарный перепад давлений на уплотнение Р0 – Р1 распределяется по всем зазорам, на первый зазор приходится небольшой перепад. Поэтому здесь развивается относительно небольшая скорость, которая и определяет невысокий расход через уплотнение. Поскольку расход через уплотнение и площадь зазора – величины постоянные для каждого отсека уплотнения (
Рис. 3. Схема лабиринтового уплотнения. Отношение скорости к объёму – величина постоянная, что следует из уравнения неразрывности:
а кривая, подчиняющаяся этому закону, называется линией Фанно (рис.4). Расход утечки через ступенчатое лабиринтовое уплотнение, кг/с, определяется по формуле:
где
Рис. 4. Линия Фанно.
Оборудование. Исходные данные. Работа выполняется на паровой турбине питательного турбонасоса ОВПТ-270А. Определяется расход утечки пара через заднее концевое уплотнение. Параметры пара перед уплотнением (давление, энтальпия) принимаются из лабораторной работы №1, как параметры за последней ступенью. Давление за уплотнением принимается равным атмосферному, Р1 = 1бар. Площадь зазора Fу определяется по результатам измерений. Коэффициент расхода μу определяется по рис. 5.
Порядок выполнения работы 1. Определить: – число гребней заднего концевого уплотнения – диаметр уплотнения dу, мм; – толщину гребня – радиальный зазор – форму гребней; – коэффициент расхода – площадь зазора уплотнения Fу = π∙ dу ∙δу, м2; – расход утечки через уплотнение
Рис.5. Коэффициент расхода 2. Построить линию Фанно методом итераций (последовательных приближений) от известного состояния пара за уплотнением в точке F (рис. 6).
Содержание отчета
Отчет должен содержать: 1) исходные данные, результаты замеров, расчеты утечки (представить в форме табл.4 Приложения); 2) тепловой процесс уплотнения, линию Фанно, расчеты.
Контрольные вопросы
1. Назначение и устройство лабиринтового уплотнения. 2. Работа лабиринтового уплотнения. 3. Тепловой процесс уплотнения. 4. Определение коэффициента расхода уплотнения 5. Ступенчатое и бесступенчатое (прямоточное) уплотнение – их достоинства и недостатки. 6. Какими мероприятиями можно снизить утечку через уплотнение? 7. Порядок расчетного построения линии Фанно.
Лабораторная работа № 3 РАСЧЕТ ТУРБИННОЙ СТУПЕНИ Оборудование. Исходные данные Выполняется тепловой расчет последней ступени многоступенчатой турбины типа ОВПТ–270А. Исходные данные ( Порядок расчета 1. На H-S диаграмме наносим точку 2. Из точки
3. Располагаемые перепады энтальпий сопловой и рабочей решеток, кДж/кг:
4. Полученные теплоперепады откладываем от точки 5. Теоретическая абсолютная скорость пара на выходе из сопел, м/с:
6. Скорость звука в потоке пара за соплами, м/с:
где 7. Число Маха сопловой решетки:
8. Коэффициент скорости сопловой решетки φ определяем по формуле: φ=0,980 - 0,009 . (b1 / l1),
где b1, l1 – хорда и высота сопловых лопаток (лаб. №1). 9. Коэффициент потерь энергии в сопловой решетке:
10. Окружная скорость рабочей решетки на среднем диаметре, м/с:
11. Действительная абсолютная скорость пара на выходе из сопел, м/с:
12. Если число Маха M1t >1 т.е. скорость истечения из сопловой решетки сверхзвуковая, возникает отклонение потока от оси сопла в косом срезе. С учетом угла отклонения δ угол выхода скорости C1 определяем по формуле Бэра:
где Cкр – критическая скорость потока, равная скорости распространения звука; V1кр – критический объем пара при критическом давлении Р1кр в минимальном сечении сопл; критическое давление
13. Если M1t <1, отклонения потока от оси сопла в косом срезе не происходит и
Рис.7. Процесс расширения пара в ступени.
14. Расход пара через сопловую решетку, кг/с: а) при M1t ≥1 б) при M1t <1 где
μ1=0,982 – 0,005(b1/l1).
Здесь b1, l1, F1 – геометрические характеристики, м, м2, принимаются по результатам лабораторной работы № 1. 15. Относительная скорость пара на входе в рабочую решетку, м/с:
16. Угол входа потока в рабочую решетку, град.:
17. В выбранном масштабе на миллиметровой бумаге строим входной треугольник скоростей.
Рис. 8. Входной треугольник скоростей.
18. Потери энергии в сопловой решетке, кДж/кг:
Полученное значение откладываем от точки А1t вверх по изобаре Р1 (рис.7). Точка А1 характеризует состояние пара перед рабочей решеткой. 19. Теоретическая относительная скорость на выходе из рабочей решетки, м/с:
20. Скорость звука в потоке за рабочей решеткой, м/с:
21. Число Маха для рабочей решетки:
22. Расчетное значение коэффициента скорости рабочей решетки ψ0 (без учета потерь от угла атаки) определяем по формуле:
ψ0=0,957 - 0,011(b2/l2).
23. Расчетное значение коэффициента потерь в рабочей решетке (без учета потерь от угла атаки):
24. Угол атаки в рабочей решетке, град.:
где 25. По рис. 10 определяем отношение действительного коэффициента потерь к расчетному
26. Действительное значение коэффициента скорости с учетом потерь от угла атаки:
27. Действительная относительная скорость пара на выходе из рабочей решетки, м/с:
28. Абсолютная скорость пара на выходе из ступени, м/с:
29. Угол направления выходной скорости, град.:
30. Потери энергии в рабочей решетке, кДж/кг:
Значение 31. В выбранном масштабе на миллиметровой бумаге строим выходной треугольник скоростей.
Рис. 9. Выходной треугольник скоростей.
32. Потери энергии с выходной скоростью, кДж/кг:
Полученное значение откладываем вверх по изобаре P2, рис.7. 33. Относительный лопаточный КПД ступени:
34. Коэффициент потерь от трения боковых поверхностей рабочего колеса в паровой среде:
где 35. Потери от трения, кДж/кг:
36. Коэффициент потерь от парциального подвода пара (только при е <1):
где 37. Потери от парциального подвода, кДж/кг:
38. Коэффициент потерь от протечек через лабиринтовые уплотнения диафрагмы:
где 39. Коэффициент потерь от протечек поверх рабочих лопаток:
40. Суммарная потеря от утечек
41. Суммарная потеря от трения, парциальности и утечек:
42. Потери 43. Полезно использованный в ступени теплоперепад, кДж/кг:
44. Внутренний относительный КПД ступени:
45. Внутренняя мощность ступени, кВт:
r -радиус входной кромки рабочего профиля; В2 - ширина рабочей решетки (лаб. №1) Рис. 10. Зависимость коэффициента потерь от угла атаки
Содержание отчета В отчете привести исходные данные, расчет ступени, тепловой процесс (рис.7) и треугольники скоростей в масштабе.
Контрольные вопросы 1. Назначение сопловых, рабочих и поворотных решеток. 2. Порядок определения коэффициентов скорости. 3. Порядок построения треугольников скоростей, определение углов и векторов скоростей. 4. Определение потерь энергии в сопловой и рабочей решетках. 5. Определение потерь от ударного входа (угла атаки). 6. Определение потерь с выходной скоростью. 7. Определение КПД 8. Определение потерь от трения, утечек и парциального подвода пара. 9. Определение КПД 10. Порядок построения реального процесса расширения ступени в H-S диаграмме. 11. Определение мощности ступени. 12. Конструкция турбины.
Лабораторная работа № 4 Общие сведения Одно из главных условий нормальной работы турбины – отсутствие вибрации, так как вибрация приводит к ускоренному износу подшипников, нарушению соединений, поломкам отдельных деталей и снижению полезной мощности. Наиболее распространенной причиной вибраций является неуравновешенность ротора. Под неуравновешенностью понимается несовпадение центра тяжести ротора с осью вращения. Это приводит к возникновению центробежной силы и вибрации. В условиях эксплуатации турбины неуравновешенность может возникать от целого ряда причин, к которым относятся прогиб вала, вылет лопаток, неравномерный износ лопаток вследствие эрозии и коррозии, неравномерный занос лопаток отложениями солей и др. Таким образом, повышенная вибрация является объективным показателем имеющихся в турбоагрегате дефектов. Для устранения неуравновешенности роторы турбин подвергают тщательной балансировке [8]. На практике приходится иметь дело с двумя видами неуравновешенности: статической и динамической. Ротор, неуравновешенные массы которого приводятся к одной массе, создающей центробежную силу при вращении, называется статически неуравновешенным. Если такой ротор установить на горизонтальных призмах или роликах, центр тяжести его неуравновешенных масс займет крайнее нижнее положение. Неуравновешенность такого ротора обнаруживается и устраняется без его вращения, т. е. в статическом состоянии. Поэтому она называется статической. Статическая балансировка достаточна для коротких роторов одноступенчатых турбин с отношением толщины диска к диаметру не более 0,2. Для статической балансировки применяются параллельные призмы, роликовые стенды. Многодисковые же роторы статически отбалансироватъ невозможно. Их подвергают динамической балансировке с вращением в специальных балансировочных станках. Рассмотрим многодисковый ротор, имеющий неуравновешенность Р в одном из дисков, например, в последнем (рис.11). Такой ротор можно уравновесить статически, если установить балансирующий груз Рб на неуравновешенный диск. Однако практически невозможно определить, какой именно из дисков неуравновешен. Поэтому может получиться так, что неуравновешенность Р и балансировочный груз Рб будут расположены в различных дисках, т.е. в разных плоскостях. В статических условиях при отсутствии вращения балансирующий груз на первом диске будет уравновешивать небаланс последнего диска. Но если привести такой, на первый, взгляд уравновешенный ротор во вращение, центробежные силы от масс Р и Рб образуют пару сил, изгибающих ротор (рис.12). Следовательно, неуравновешенность статически уравновешенного многодискового ротора обнаруживается только при вращении. Поэтому ее называют динамической неуравновешенностью. Чтобы устранить динамическую неуравновешенность, достаточно в двух любых дисках установить равные грузы, не нарушающие заранее проведенной статической балансировки, но изгибающие вал в направлении, противоположном изгибу от сил Р и Рб. Правильный подбор этих грузов позволяет ликвидировать динамический изгиб вала. Эта операция называется динамической балансировкой. Балансирующие грузы чаще всего устанавливают в первом и последнем дисках, так как они более доступны и максимально удалены друг от друга. Таким образом, задачей динамической балансировки является определение места установки и веса балансирующих грузов, кото
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1675; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.24.70 (0.014 с.) |

 Лабораторная работа № 1
Лабораторная работа № 1 – ширина входного сечения каналов; Оmin – ширина минимального сечения расширяющегося канала;
– ширина входного сечения каналов; Оmin – ширина минимального сечения расширяющегося канала;  – лопаточные (скелетные) углы наклона входной и выходной кромки профиля.
– лопаточные (скелетные) углы наклона входной и выходной кромки профиля.
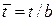 –относительный шаг решетки;
–относительный шаг решетки;  –относительная высота решетки;
–относительная высота решетки; 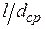 –веерность решетки;
–веерность решетки;  –относительная толщина выходной кромки;
–относительная толщина выходной кромки;  –степень расширения канала;
–степень расширения канала;  ,
,  - эффективные углы потока при выходе из сопловой и рабочей решеток соответственно.
- эффективные углы потока при выходе из сопловой и рабочей решеток соответственно. не совпадает со скелетным углом профиля лопатки
не совпадает со скелетным углом профиля лопатки  , то разность
, то разность 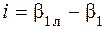 называется углом атаки. При
называется углом атаки. При  имеет место безударное натекание потока, обеспечивающее наилучшее обтекание профиля, к чему и следует стремиться. Чем больше угол атаки, тем хуже обтекается профиль, тем больше потери энергии в рабочей решетке, тем ниже КПД ступени.
имеет место безударное натекание потока, обеспечивающее наилучшее обтекание профиля, к чему и следует стремиться. Чем больше угол атаки, тем хуже обтекается профиль, тем больше потери энергии в рабочей решетке, тем ниже КПД ступени.

 - число сопловых каналов.
- число сопловых каналов.


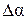 или
или  и безразмерной скоростью потока (числом Маха).
и безразмерной скоростью потока (числом Маха). – группа А (дозвуковые);
– группа А (дозвуковые); – группа Б (околозвуковые);
– группа Б (околозвуковые); – группа В (сверхзвуковые);
– группа В (сверхзвуковые); – группа Р (расширяющиеся).
– группа Р (расширяющиеся).

 – давление условно заторможенного потока перед сопловой и рабочей решеткой.
– давление условно заторможенного потока перед сопловой и рабочей решеткой. ,
, – скорость распространения звука в потоке пара соответственно за сопловой и рабочей решеткой. Здесь Р1, Р2 – [Па];
– скорость распространения звука в потоке пара соответственно за сопловой и рабочей решеткой. Здесь Р1, Р2 – [Па];  = 1,3 – показатель изоэнтропы.
= 1,3 – показатель изоэнтропы.
 – кинематическая вязкость пара на выходе из сопловой и рабочей решеток;
– кинематическая вязкость пара на выходе из сопловой и рабочей решеток;  Здесь
Здесь  ,
,  – динамическая вязкость (таблица 3 Приложения).
– динамическая вязкость (таблица 3 Приложения).
 ,
, – окружная скорость;
– окружная скорость;  – фиктивная скорость, эквивалентная располагаемому теплоперепаду ступени.
– фиктивная скорость, эквивалентная располагаемому теплоперепаду ступени. ;
; ;
; ;
; .
. бар;
бар;  оC; Р2 = 4–8 бар; n = 9000–12000 об/мин; ρТ = 0,05–0,20.
оC; Р2 = 4–8 бар; n = 9000–12000 об/мин; ρТ = 0,05–0,20.
 расход утечки через уплотнение, кг/с; V – удельный объем, м3/кг;
расход утечки через уплотнение, кг/с; V – удельный объем, м3/кг;  площадь зазора в уплотнении, м2; С –скорость пара в зазоре, м/с;
площадь зазора в уплотнении, м2; С –скорость пара в зазоре, м/с; 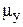 – коэффициент расхода уплотнения.
– коэффициент расхода уплотнения.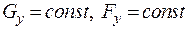 ), увеличение удельного объёма V по мере понижения давления сопровождается таким же увеличением скорости С от зазора к зазору. Поэтому перепад энтальпий
), увеличение удельного объёма V по мере понижения давления сопровождается таким же увеличением скорости С от зазора к зазору. Поэтому перепад энтальпий  срабатываемый в каждом последующем зазоре, больше, чем в предыдущем.
срабатываемый в каждом последующем зазоре, больше, чем в предыдущем.

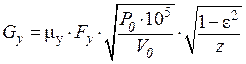 ,
, коэффициент расхода уплотнения, который зависит от формы гребней, их толщины и радиального зазора (рис. 5); Fу = π∙ dу ∙δу – площадь зазора, м2; Р0, V0 - параметры перед уплотнением, бар, м3/кг;
коэффициент расхода уплотнения, который зависит от формы гребней, их толщины и радиального зазора (рис. 5); Fу = π∙ dу ∙δу – площадь зазора, м2; Р0, V0 - параметры перед уплотнением, бар, м3/кг;
 отношение давлений уплотнения;
отношение давлений уплотнения;  число гребней. Величина радиального зазора
число гребней. Величина радиального зазора  но не меньше 0,2–0,3мм. Толщина гребня
но не меньше 0,2–0,3мм. Толщина гребня  обычно составляет 0,2–0,3мм.
обычно составляет 0,2–0,3мм. ;
; , мм;
, мм; по рис. 5;
по рис. 5; , кг/с.
, кг/с.
 .
. ), а также геометрические характеристики решеток, необходимые для расчета (средний диаметр, лопаточные углы и т.д.), заданы и определены в лабораторной работе № 1.
), а также геометрические характеристики решеток, необходимые для расчета (средний диаметр, лопаточные углы и т.д.), заданы и определены в лабораторной работе № 1. , соответствующую состоянию пара перед ступенью (по параметрам пара
, соответствующую состоянию пара перед ступенью (по параметрам пара  рис.7) и определяем энтальпию
рис.7) и определяем энтальпию  .
. определяем энтальпию
определяем энтальпию  , удельный объем
, удельный объем  и температуру
и температуру  . Располагаемый перепад энтальпий ступени, кДж/кг:
. Располагаемый перепад энтальпий ступени, кДж/кг:

 на H-S диаграмме (рис.7) и определяем параметры пара за сопловой решеткой в точке
на H-S диаграмме (рис.7) и определяем параметры пара за сопловой решеткой в точке  (Р1, V1t, t1t).
(Р1, V1t, t1t).

 – показатель изоэнтропы, для перегретого пара k =1,3.
– показатель изоэнтропы, для перегретого пара k =1,3.





 0,546. Критический объем можно определить на H-S диаграмме по давлению Р1кр или из уравнения изоэнтропы:
0,546. Критический объем можно определить на H-S диаграмме по давлению Р1кр или из уравнения изоэнтропы:


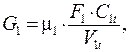
 – коэффициент расхода сопловой решетки, определяется по формуле:
– коэффициент расхода сопловой решетки, определяется по формуле:








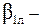 лопаточный угол наклона входной кромки, принимаем из лабораторной работы № 1.
лопаточный угол наклона входной кромки, принимаем из лабораторной работы № 1. , а затем – действительное значение коэффициента потерь
, а затем – действительное значение коэффициента потерь  с учетом потерь от угла атаки. Здесь
с учетом потерь от угла атаки. Здесь





 .
. откладываем вверх по изобаре P2, рис.7.
откладываем вверх по изобаре P2, рис.7.



 =0,0008–0,0012;
=0,0008–0,0012;  принимаем из лабораторной работы № 1.
принимаем из лабораторной работы № 1.
 ,
, = 0,065,
= 0,065,  = 0,25;
= 0,25;  геометрические характеристики, принимаем из лабораторной работы № 1.
геометрические характеристики, принимаем из лабораторной работы № 1.
 ,
, площадь зазора в уплотнении, м2;
площадь зазора в уплотнении, м2;  диаметр уплотнения;
диаметр уплотнения;  = 0,005м–радиальный зазор уплотнения; μ1– коэффициент расхода сопловой решетки; μу=0,7–0,75–коэффициент расхода уплотнения;
= 0,005м–радиальный зазор уплотнения; μ1– коэффициент расхода сопловой решетки; μу=0,7–0,75–коэффициент расхода уплотнения;  число гребней диафрагменного уплотнения.
число гребней диафрагменного уплотнения. , где
, где
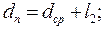 δr = 0,5мм – радиальный зазор над рабочими лопатками;
δr = 0,5мм – радиальный зазор над рабочими лопатками;  осевой зазор;
осевой зазор;  число гребней периферийного уплотнения.
число гребней периферийного уплотнения.

 откладываем вверх по изобаре Р2, рис.7.
откладываем вверх по изобаре Р2, рис.7.



 . Какие потери он учитывает?
. Какие потери он учитывает? . Какие потери он учитывает?
. Какие потери он учитывает?


