
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Cреднего квадратического отклоненияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть случайная величина Х распределена в генеральной совокупности по нормальному закону. По данным выборки можно найти для нее Пусть Преобразуем неравенство в скобках к виду, удобному для использования готовых таблиц. Неравенство
где Предполагая, что Умножая обе части неравенства на
Можно показать, что плотность распределения величины
Поэтому вероятность осуществления неравенства (7.10) равна
где
Интеграл Замечание. Если Пример. В условиях примера (стр.106) найти доверительный интервал, накрывающий генеральное среднее квадратическое отклонение По данным выборки объема n =15 исправленное среднее квадратическое отклонение
УПРОЩЕННЫЕ МЕТОДЫ РАСЧЕТА СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ВЫБОРКИ 8.1. Вариационный ряд с равноотстоящим вариантами. Условные варианты Непосредственное использование значений признака (вариант), произвольным образом выбранных из генеральной совокупности, приводит к существенным затруднениям при вычислении статистических характеристик выборки. Упрощенные методы их расчета базируются на замене первоначальных вариант xi условными Здесь С – так называемый “ложный нуль” (новое начало отсчета), Рассмотрим сначала вариационный ряд с равноотстоящими вариантами. Это означает, что
Пример. Найти условные варианты статистического распределения выборки
Принимаем С = 155,2. Очевидно ∆ = 5. Условные варианты будут равны: Проводить вычисления с ними, конечно проще, чем с первоначальными значениями признака xi . Эмпирические моменты Аналогично числовым характеристикам (теоретическим моментам рас-пределения генеральной совокупности), применяемым в теории вероятностей, в статистике рассматривают эмпирические моменты выборочного распределения. Обычным эмпирическим моментом порядка k называется среднее значение к – ых степеней разностей (Х – С):
Здесь ni - частота варианты xi, Начальным эмпирическим моментом порядка k называется обычный эмпирический момент k – го порядка при С = 0, то есть
Очевидно, что М0 = 1, Центральным эмпирическим моментом порядка k называется обычный момент k – го порядка, если
Первые четыре центральных момента выражаются через обычные моменты следующим образом:
Непосредственное вычисление центральных эмпирических моментов достаточно трудоемко. Для упрощения расчетов заменяют первоначальные варианты условными. Тогда приходят к так называемым условным эмпирическим моментам. Условным эмпирическим моментом порядка k называется начальный эмпирический момент k - го порядка для условных вариант:
В частноcти, поэтому
Очевидно,
Поэтому центральные моменты через условные будут выражаться по формулам:
Использование полученных формул позволяет значительно упростить вычисление оценок генеральной средней и генеральной дисперсии. 8.3. Сведение первоначальных вариант к равноотстоящим. Метод произведений Как правило, значения признака (варианты), регистрируемые в опытах, не являются равноотстоящими. При этом условные варианты получаются не целыми числами. Для сведения первоначальных вариант к равноотстоящим применяется следующий прием: Интервал, в котором заключены все наблюдавшиеся значения признака, делится на несколько равных частичных интервалов (желательно, чтобы в каждый частичный интервал попало не менее 10 первоначальных вариант); определяются середины частичных интервалов, которые и образуют последовательность равноотстоящих вариант; в качестве частоты каждой “новой” варианты принимается общее число первоначальных вариант, которые попали в соответствующий частичный интервал (с учетом замечания на стр. 98). При обработке опытных данных практически всегда приходится вычислять Пример. Из текущей продукции токарного автомата, обрабатывающего валики, сделана выборка объемом n =100 (см. таблицу 4). Требуется найти выборочную среднюю Разобьем весь интервал изменения значений признака (диаметра валика - Х) 15,20 – 15,60 мм на 8 частичных интервалов: 15,20 – 15,25; 15,25-15,30; …,15,55-15,60. Приняв середины частичных интервалов в качестве новых вариант, получим вариационный ряд из равноотстоящих вариант: Таблица 7
В четвертом столбце таблицы указаны условные варианты В качестве “ложного нуля” принята варианта Очевидно, ∆ = 0,05. В 5-ом, 6-ом и 7-ом столбцах таблицы помещены величины Контроль правильности вычислений производится следующим образом:
или 410,5 = 371,5 + 2∙(-30,5) + 100; 410,5 ≡ 410,5. По данным таблицы условные эмпирические моменты первого и второго порядков будут равны
Окончательно получим
Непосредственный подсчет выборочной средней и второго центрального момента по первоначальным значениям признака из таблицы 4 с использованием формул (7.1), (8.1) приводит к следующим результатам:
Как видно, замена первоначальных вариант равноотстоящими не приводит к существенным ошибкам, но при этом объем вычислений заметно сокращается.
КРИТЕРИИ СОГЛАСИЯ Между статистическим распределением случайной величины, которое строится всегда по ограниченному числу опытов, и предполагаемым теоретическим распределением неизбежно некоторое расхождение. Оно порождается либо случайными причинами, обусловленными ограниченным числом наблюдений, либо может быть неслучайным и связано с тем, что принимаемая гипотеза о предполагаемом законе распределения случайной величины противоречит опытным данным. Для оценки близости теоретического и эмпирического распределений и применяют критерии согласия. Они позволяют установить, является ли расхождение эмпирического и теоретического распределений несущественным (случайным) или значимым (неслучайным). Идея их построения заключается в следующем. Чтобы принять (или отвергнуть) некоторую гипотезу Н о том, что случайная величина Х подчинена определенному закону распределения с функцией F (x), вводят в рассмотрение величину W, которая характеризует меру расхождения между теоретической F (x) и эмпирической F (x) функциями распределения. Очевидно, W - случайная величина, закон распределения которой зависит от закона распределения Х и числа опытов n. Пусть в результате данной серии опытов установлено, что W приняла некоторое значение w. Предположим, что принятая гипотеза верна и найдем вероятность того, что расхождение W между эмпирическим и теоретическим распределениями за счет чисто случайных причин (связанных с недостаточным объемом опытных данных) не меньше, чем наблюдавшееся для данной серии опытов расхождение w, то есть, что W ≥ w. Если эта вероятность мала, то это значит, что причины расхождения неслучайны, и гипотеза о предполагаемом характере распределения случайной величины противоречит опытным данным, то есть ее надо отбросить, и наоборот. Вопрос о том, как мала или велика должна быть указанная вероятность, решается не из математических, а из практических соображений с учетом конкретных условий задачи. Обычно в качестве практически невозможных отклонений принимают такие, вероятность которых не превосходит 0,05 или 0,01 и т.п. Такую вероятность называют уровнем значимости. Итак, если В зависимости от того, какая величина принимается в качестве меры W, различают те или иные критерии согласия. Ниже будут рассмотрены лишь два из них, наиболее часто применяемые. 9.1. Критерий Допустим, что произведено n опытов над случайной величиной Х. Всю область изменения значений Х разобъем на S частичных интервалов или разрядов (в случае непрерывной величины) или групп, состоящих из отдельных значений дискретной величины. Подсчитаем эмпирические частоты ni тех значений xi, которые попали в i -ый разряд (группу). Предположим теперь, что для Х принят некоторый закон распределения. Тогда можно найти вероятность попадания Х в каждый из S разрядов: Критерий
Очевидно, величина Как известно, в теории вероятностей распределением
Кривые распределения
Здесь Распределение Можно показать, что закон распределения случайной величины W приближается к закону распределения Для распределения Пример. Произведено 250 измерений с точностью до 1мк диаметра валиков, обработанных на токарном автомате. В таблице 8 приведены отклонения Х от номинального размера, разбитые на интервалы по 5 мк в каждом, и числа деталей Таблица 8
1. По данным выборки методом произведений найдем оценки генеральной средней и генеральной дисперсии:
Теоретические частоты для предполагаемого нормального распределения определяются по формуле
где функция
Таблица 9
Определяем меру расхождения Таблица 10
При числе степеней свободы K = S – 3 = 2 и уровне значимости 0,05 по таблице Приложения 5 находим Замечание. При применении критерия Критерий Колмогорова В качестве меры расхождения между эмпирическим и теоретическим распределениями можно рассматривать максимум модуля разности между эмпирической и теоретической функциями распределения:
А.Н.Колмогоровым было показано, что независимо от вида функции F(x) при неограниченном возрастании n (а практически при n не менее нескольких десятков) интегральная функция распределения случайной величины Обозначим конкретное значение Пусть, например, уровень значимости равен 0,01. Тогда, если Критерий Колмогорова может быть использован также для решения вопроса о том, принадлежат ли две выборки объемов При этом находят величину
где Замечание. Достоинством критерия Колмогорова является его простота, а недостаток состоит в том, что его можно применять только, если предполагаемая теоретическая функция распределения F (x) полностью известна (то есть известен не только вид распределения, но и все входящие в него параметры). Пример. Имеются две группы однородных деталей, изготовленных одним станком, по 60 штук в каждой. Результаты измерений длины Х после группировки данных приведены в таблице 11. Таблица 11
Проверить с помощью критерия Колмогорова гипотезу о том, что обе выборки принадлежат одной генеральной совокупности. 1. Эмпирические функции распределения 2. Максимум модуля разности между ними, как видно из таблицы 11, равен 3. Определив Следовательно, при уровне значимости 0,01 гипотеза о том, что обе выборки принадлежат одной генеральной совокупности, не опровергается.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 710; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.013 с.) |

 Требуется найти доверительный интервал, накрывающий неизвестное среднее квадратическое отклонение генеральной совокупности
Требуется найти доверительный интервал, накрывающий неизвестное среднее квадратическое отклонение генеральной совокупности 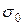 c заданной надежностью γ.
c заданной надежностью γ. или
или  .
.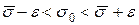 равносильно неравенству
равносильно неравенству (7.9)
(7.9)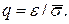
 перепишем (6.9) в виде
перепишем (6.9) в виде 
 и обозначая
и обозначая  , получим
, получим . (7.10)
. (7.10) имеет вид [1]
имеет вид [1]



 табулирован. Вычислив по данным выборки
табулирован. Вычислив по данным выборки 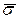 и зная n и γ, можно по таблицам найти
и зная n и γ, можно по таблицам найти  , а затем определить доверительный интервал
, а затем определить доверительный интервал 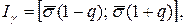 в котором с надежностью γ заключено неизвестное значение
в котором с надежностью γ заключено неизвестное значение  (см. Приложение 4).
(см. Приложение 4). то неравенство (7.9) следует заменить неравенством
то неравенство (7.9) следует заменить неравенством  . Можно показать, что в этом случае значения
. Можно показать, что в этом случае значения  могут быть найдены из уравнения
могут быть найдены из уравнения 
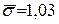 мм. При
мм. При  и
и  по таблице Приложения 4 найдем
по таблице Приложения 4 найдем  . Так как
. Так как 

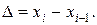 В качестве ложного нуля выбирают значение признака, имеющее наибольшую частоту. Оно обычно располагается примерно в середине вариационного ряда.
В качестве ложного нуля выбирают значение признака, имеющее наибольшую частоту. Оно обычно располагается примерно в середине вариационного ряда. для любого i =1,2... Тогда условные варианты будут целыми числами. Действительно, взяв в качестве С произвольную варианту xm, получим
для любого i =1,2... Тогда условные варианты будут целыми числами. Действительно, взяв в качестве С произвольную варианту xm, получим - целое число.
- целое число.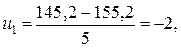 u2 = -1, u3 = 0, u4 = 1, u5 = 2.
u2 = -1, u3 = 0, u4 = 1, u5 = 2. .
. - объем выборки, С – произвольное постоянное число (“ложный нуль”).
- объем выборки, С – произвольное постоянное число (“ложный нуль”).
 - выборочная средняя.
- выборочная средняя.
 (8.1)
(8.1)

 ,
, .
.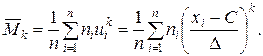
 ,
, .
.
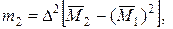


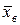 и
и  . Если объем выборки достаточно большой, то для сокращения вычислений обычно применяется метод произведений. Последовательность нахождения
. Если объем выборки достаточно большой, то для сокращения вычислений обычно применяется метод произведений. Последовательность нахождения  и второй центральный момент m 2.
и второй центральный момент m 2.

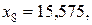 частоты которых:
частоты которых: 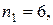 …,
…, 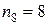 (см. таблицу 7).
(см. таблицу 7).




 .
.
 В нижней строке указаны суммы соответствующих столбцов.
В нижней строке указаны суммы соответствующих столбцов.






 (или 0,05 и т.п.), то выдвинутая гипотеза о теоретическом законе распределения противоречит опытным данным и должна быть отброшена и наоборот, если
(или 0,05 и т.п.), то выдвинутая гипотеза о теоретическом законе распределения противоречит опытным данным и должна быть отброшена и наоборот, если  , то гипотезу Н можно принять для данного уровня значимости.
, то гипотезу Н можно принять для данного уровня значимости. Пирсона
Пирсона Величины
Величины  называются теоретическими (выравнивающими) частотами.
называются теоретическими (выравнивающими) частотами. .
. к
к  .
. , каждая из которых подчинена нормированному нормальному закону. Плотность вероятностей этой величины имеет вид:
, каждая из которых подчинена нормированному нормальному закону. Плотность вероятностей этой величины имеет вид:

 для различных значений k показаны на рисунке.
для различных значений k показаны на рисунке.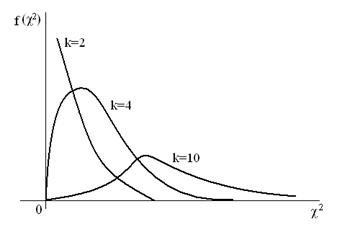
 - гамма - функция, k - число степеней свободы,
- гамма - функция, k - число степеней свободы,  , где S – число разрядов (групп), на которые делится диапазон всех наблюдавшихся значений случайной величины, m – число параметров предполагаемого теоретического распределения (например, для нормального закона m =2).
, где S – число разрядов (групп), на которые делится диапазон всех наблюдавшихся значений случайной величины, m – число параметров предполагаемого теоретического распределения (например, для нормального закона m =2).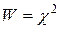 примет значение, не меньше, чем вычисленное по данным опытов число
примет значение, не меньше, чем вычисленное по данным опытов число  . Можно также сравнить наблюдаемые значения критерия
. Можно также сравнить наблюдаемые значения критерия  с, так называемыми, критическими точками распределения
с, так называемыми, критическими точками распределения  если
если  - нет оснований отвергать гипотезу, если
- нет оснований отвергать гипотезу, если  - принятую гипотезу отвергают (см. Приложение 5).
- принятую гипотезу отвергают (см. Приложение 5).



 табулирована (см.Приложение 1),
табулирована (см.Приложение 1),  Вычисления сведем в таблицу 9.
Вычисления сведем в таблицу 9.





 Так как наблюдаемое значение критерия
Так как наблюдаемое значение критерия  , гипотеза о соответствии данных наблюдений нормальному закону распределения признака в генеральной совокупности не опровергается.
, гипотеза о соответствии данных наблюдений нормальному закону распределения признака в генеральной совокупности не опровергается.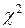 Пирсона необходимо, чтобы как общее число значений признака n, так и числа наблюдений в отдельных разрядах
Пирсона необходимо, чтобы как общее число значений признака n, так и числа наблюдений в отдельных разрядах  были достаточно велики. Практически необходимо, чтобы n > 50 – 60, а
были достаточно велики. Практически необходимо, чтобы n > 50 – 60, а  Если какое-либо из
Если какое-либо из  .
. приближается к функции
приближается к функции 
 , полученное в данной серии опытов, через
, полученное в данной серии опытов, через  Тогда
Тогда  Значения вероятности
Значения вероятности  табулированы и приводятся в литературе.
табулированы и приводятся в литературе.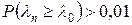 , то гипотеза о том, что Х имеет функцию распределения
, то гипотеза о том, что Х имеет функцию распределения  , не противоречит опытным данным, и наоборот.
, не противоречит опытным данным, и наоборот. и
и  одной генеральной совокупности.
одной генеральной совокупности.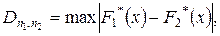
 - эмпирические функции распределения 1-ой и 2-ой выборок соответственно (i =1,2), а величина
- эмпирические функции распределения 1-ой и 2-ой выборок соответственно (i =1,2), а величина  определяется из выражения
определяется из выражения 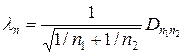 и при
и при  имеет асимптотической функцией распределения функцию
имеет асимптотической функцией распределения функцию  критерия Колмогорова.
критерия Колмогорова.
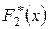


 , где
, где  и, следовательно,
и, следовательно, 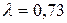 , по таблице Приложения 6 для данного значения
, по таблице Приложения 6 для данного значения 



