
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Локальная и интегральная теоремы ЛапласаСодержание книги
Поиск на нашем сайте
При больших значениях n непосредственное применение формулы Бернулли затруднительно из-за вычислительных трудностей. В этом слу-чае применяют локальную теорему Лапласа, которая справедлива, если число испытаний n достаточно велико (практически при Если вероятность p появления случайного события A в каждом испы-тании постоянна, то вероятность появления события k раз в n испытаниях приближенно (тем точнее, чем больше n) равна
где Функция Обобщением локальной теоремы Лапласа является интегральная теорема Лапласа. Она позволяет найти вероятность
где Интегральную формулу Лапласа можно представить в виде, удобном для вычислений:
где функция Пример. Найти вероятность того, что событие А (переключение передач) наступит 70 раз на трассе длиной 256 км, если вероятность пере-ключения на каждом км этой трассы равна 0,25. Решение. Число испытаний n соответствует числу км на трассе. Так как n=256 велико, применим локальную теорему Лапласа. По условию
Тогда По таблице находим
Пример. Вероятность появления события А в каждом из 200 незави-симых испытаний постоянна и равна Решение. Так как n велико и заданы интервалы изменения k, приме-ним интегральную теорему Лапласа. a) по условию Вычислим
Искомая вероятность равна
По таблице приложения 2 линейной интерполяцией найдем
б) В рассматриваемом случае следует принять Поэтому и по таблице приложения 2
в) События “ А появилось не менее 150 раз” и “ А появилось не более 149 раз” противоположны. Поэтому
Пример. Вероятность изготовления годной детали на станке равна 0,9. Сколько нужно обработать деталей, чтобы с вероятностью 0,98 можно было ожидать, что не менее 150 деталей будут годными? Решение. По условию Применяя интегральную формулу Лапласа, получим
или
Так как заведомо По таблице приложения 2 находим
Решая это уравнение как квадратное относительно Задачи для самостоятельного решения 1. (Задача Даламбера). Испытание состоит в двукратном подбрасывании монеты. Какова вероятность того, что в результате испытания герб выпадет хотя бы один раз? 2. Сколькими способами можно распределить 6 различных предметов между тремя лицами так, чтобы каждый получил по два предмета? 3. Лотерея выпущена на общую сумму n рублей. Цена одного билета r рублей. Ценные выигрыши падают на c билетов. Найти вероятность ценного выигрыша на один билет. 4. Задумано двузначное число, цифры которого различны. Найти вероятность того, что задуманным числом окажется: а) случайно названное двузначное число; б) случайно названное двузначное число, цифры которого различны. 5. Брошены 3 монеты. Найти вероятность того, что выпадут 2 герба. 6. За круглый стол в случайном порядке рассаживаются 4 мужчин и 4 женщины. Найти вероятность того, что никакие два лица одинакового пола не окажутся рядом. 7. Студенты данного курса изучают 8 предметов. В расписание занятий можно поставить 4 предмета в день. Сколько существует различных вариантов составления расписания на день? 8. Каждая из цифр 1, 2, 3, 4, 5 написана на одной карточке. Извлекаются наугад три карточки. Найти вероятность того, что составленное из них трехзначное число окажется четным. 9. В замке на общей оси 4 диска, каждый из которых разделен на 6 секторов, на которых написаны различные цифры. Замок открывается только в том случае, если диски установлены так, что цифры на них составляют определенное четырехзначное число. Найти вероятность того, что при произвольной установке дисков замок будет открыт. 10. Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера. Полученные кубики тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет иметь две окрашенные грани. 11. При наборе телефонного номер абонент забыл две последние цифры и набрал их наугад, помня только, что они нечетные и разные. Найти вероятность того, что номер набран правильно. 12. На стеллаже 100 деталей, из них 10 бракованных. Наудачу извлечены 3 детали. Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных. 13. Из последовательности чисел 1,2,…, n наудачу выбираются 2 числа. Найти вероятность того, что одно из них меньше k, а другое больше k, где 14. В шахматном турнире участвуют 20 человек, которые по жребию распределяются в две группы по 10 человек. Найти вероятность того, что: а) два наиболее сильных участника будут играть в разных группах; б) четыре наиболее сильных участника попадут по два в разные груп- пы. 15. При перевозке 8 изделий одного типа и 12 изделий другого типа повреждены два изделия. Какое событие более вероятно: а) повреждены изделия одного типа; б) разных типов. 16. В комплекте m стандартных и n нестандартных деталей. Наугад три раза извлекают деталь. Найти вероятность того, что все три извлеченных детали окажутся стандартными, если: а) - после каждого извлечения деталь возвращают в комплект; б) - извлеченные детали назад не возвращаются. 17. В урне a белых и b черных шаров. Из нее наугад 2 раза извлекают по одному шару. Найти вероятность того, что оба извлеченных шара будут одинакового цвета, если первый шар в урну: а) возвращают; б) не возвращают. 18. Студент знает 20 из 30 вопросов программы. В выбранном им наугад экзаменационном билете 3 вопроса. Найти вероятность того, что студент: а) не сдаст экзамен (не ответит ни на один вопрос); б) сдаст на “удовлетворительно” (ответит на один вопрос); в) сдаст на “хорошо” (ответит на 2 вопроса); г) сдаст на “отлично” (ответит на все три вопроса). 19. Некто купил карточку “Спортлото” и отметил в ней 6 из имеющихся 49 номеров, после чего в тираже разыгрывались 6 “выигравших” номеров из 49. Найти вероятности следующих событий:
выигравших номера из 49; 49; 20. В лифт семиэтажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Найти вероятности следующих событий: а) все пассажиры выйдут на 4-ом этаже; б) все пассажиры выйдут одновременно; в) все пассажиры выйдут на различных этажах 21. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг: а) квадрата; б) правильного треугольника в) правильного шестиугольника. (Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения внутри круга). 22. В равнобедренный прямоугольный треугольник вписан круг. Наудачу брошена точка. Найти вероятность попадания точки в область треугольника, не принадлежащую кругу. 23. В ромб со стороной a и углом при вершине основания 24. В круг радиуса R вписан квадрат. Найти вероятность того, что брошенные наугад внутрь круга 2 точки окажутся внутри квадрата. 25. Полет космического корабля можно считать застрахованным от столк-новения с метеоритными частицами, если вероятность такой “встречи” 26. Два лица договорились о встрече между 18 и 19 часами с условием, что пришедший раньше ждет другого в течение 15 мин, после чего уходит. Найти вероятность того, что встреча состоится, если приход каждого из лиц в течение указанного часа может произойти в любое время. 27. На отрезке OA длины L числовой оси Ox поставлены две точки 28. При движении автомобиля под его левые и правые колеса попадают препятствия (выступы и впадины дорожного полотна). Пусть A – событие, состоящее в попадании препятствия под левое колесо, B – под правое. Какой смысл имеют события: a) A+B; b) AB, c) 29. К механизмам управления автомобилем относятся рулевое управление и две тормозные системы. Событие A – исправно рулевое управление, 30. Пусть 31. При включении зажигания двигатель начинает работать с вероятностью p. Найти: а) вероятность того, что двигатель начнет работать при втором включении зажигания; б) вероятность того, что для ввода двигателя в работу придется включить зажигание не более двух раз. 32. К автобусной остановке каждые 6 мин. подходит автобус маршрута a и каждые 9 мин. - автобусмаршрута b. Предполагая моменты прихода на остановку автобусов независимыми, найти вероятность того, что: а) первый подошедший автобус окажется автобусом маршрута a; б) ав- тобус какого – либо маршрута подойдет к остановке в течение 3-х минут. 33. Студент знает 20 из 30 вопросов программы. Найти вероятность того, что студент даст правильный ответ на три последовательно предложенные ему один за другим вопроса программы. 34. Студент знает не все экзаменационные билеты. В каком случае вероятность вытащить неизвестный билет будет для него меньше: когда он тащит билет первым или последним? 35. 20 человек, разыгрывая одну вещь, по очереди тянут жребий. Какова вероятность выиграть у первого второго и т. д. участников? 36. Имеются две урны: в первой a белых и b черных шаров, во второй - c белых и d черных шаров. Из каждой урны наугад выбирают по одному шару. Определить вероятности следующих событий: а) – оба шара разных цветов; б) – оба шара одного цвета. 37. В урне один белый и два черных шара. Из урны два игрока поочередно наугад извлекают шар, причем после каждого извлечения шар возвращается в урну. Выигравшим считается тот, кто первым извлечет белый шар. Найти вероятность выигрыша для первого игрока, если максимальное число попыток равно трем. 38. В урне 2 белых и 4 черных шара. Два игрока поочередно извлекают шар (без возвращения). Выигрывает тот, кто первым вынет белый шар. Найти вероятность выигрыша для каждого участника игры. 39. В одной коробке 5 коротких и 10 длинных болтов, в другой коробке 10 коротких и 5 длинных болтов. Найти вероятность того, что хотя бы из одной коробки будет вынут один короткий болт, если из каждой коробки вынуть по одному болту. 40. Производятся испытания некоторого устройства. При каждом испытании устройство выходит из строя с вероятностью p. После первого выхода из строя устройство ремонтируется, после второго – признается негодным. Найти вероятность того, что устройство окончательно выйдет из строя в точности при k - ом испытании. 41. Прибор состоит из трех узлов. В первом узле
42. Завод изготавливает изделия, каждое из которых с вероятностью 43. Для повышения надежности устройства оно дублируется (n -1) другими такими же устройствами (см. рис.). Надежность (вероятность безотказной работы) каждого устройства равна p. Найти надежность системы. Сколько надо взять устройств, чтобы повысить надежность системы до заданной величины
44. В течение времени t эксплуатировалось N автомашин. Каждая из них имеет надежность p и выходит из строя независимо от других. Найти вероятность того, что механик, приступающий по окончании времени t к ремонту неисправных автомашин, не справится со своей задачей за время 45. Автомашину с преступниками преследуют две милицейские машины. Преступники начинают стрельбу и производят по одному выстрелу по милицейским машинам, подбивая их с вероятностью 46. Какова вероятность того, что хотя бы один из трех основных узлов (рама, передняя и задняя оси, подвеска) ходовой части автомобиля останется исправным после 10000 км пробега, если известно, что для каждого узла такая вероятность равна 0,4? 47. Игральная кость брошена n раз. Чему равна вероятность того, что: а) шестерка выпадет один раз; б) шестерка выпадет хотя бы один раз; в) шестерка выпадет не менее двух раз. 48. Электрическая цепь состоит из восьми параллельно включенных потребителей. Вероятность работы каждого из них равна 0,8. Взаимное влияние в цепи отсутствует. Найти вероятность того, что откажет не менее половины потребителей. Сколько потребителей надо включить параллельно, чтобы с вероятностью, не меньшей 0,99 быть уверенным в том, что не откажет хотя бы один из них? 49. Вероятность попадания в цель при каждом выстреле равна 0,1. Сколько выстрелов надо произвести, чтобы с вероятностью 0,9 быть уверенным в том, что число попаданий будет не менее 10? 50. На рисунках а) и б) изображены схемы дорог, Турист выходит из пункта B, выбирая наугад на разветвлении дорог один из возможных маршрутов. Какова вероятность того, что он беспрепятственно (то есть не заходя ни в один тупик) попадет в пункт A? а) б)
51. Из урны, содержащей M белых и N-M черных шаров, один шар не- известного цвета утерян. Какова вероятность извлечь наудачу из урны белый шар? 52. Имеются две урны: в первой a белых и b черных шаров, во второй c белых и d черных шаров. Из первой урны во вторую перекладывают, не глядя, один шар. Затем из второй урны извлекают наудачу один шар. Найти вероятность того, что этот шар будет белым. 53. В автобусе едут n пассажиров На следующей остановке каждый из них выходит с вероятностью p. Кроме того, в автобус с вероятностью 54. Группа студентов состоит из 4-х отличников, 6-ти хорошо успевающих и 15 занимающихся слабо. Отличники на предстоящем экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся студенты могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад один студент. Найти вероятность того, что он получит хорошую или отличную оценку. 55. Имеются два комплекта деталей: в первом 5 стандартных и 3 нестандартных детали, во втором 6 стандартных и 2 нестандартных детали. Из первого комплекта во второй переложили, не глядя, две детали, а затем из второго комплекта взяли одну деталь. Какова вероятность того, что она будет стандартной? 56. Имеются N лунок, по которым случайным образом разбрасываются M шариков. Найти вероятность того, что в данную лунку попадет k шариков. 57. Испытание заключается в бросании трех игральных костей. Найти вероятность того, что при пяти испытаниях ровно в трех появится в точности по две шестерки. 58. Производится стрельба по цели тремя снарядами. Снаряды попадают в цель независимо друг от друга. Для каждого снаряда вероятность попадания в цель равна 0,4. Если в цель попал один снаряд, он поражает цель (выводит ее из строя) с вероятностью 0,3; если два снаряда, они поражают цель с вероятностью 0,7; если три снаряда – с вероятностью 0,9. Найти полную вероятность поражения цели. 59. Колонна из трех грузовых машин и ведущего тягача послана для доставки грузов на военный объект. Без тягача выход к объекту невозможен. В пути автомашины проходят через зону обстрела, в которой каждая из них может быть подбита с вероятностью 0,3. После прибытия на объект все 4 машины разгружаются независимо. Вероятность полной разгрузки каждой из них за заданное время равна 0,7. Какова вероятность того, что весь груз будет благополучно передан на объект? 60. Имеются 3 урны: в первой a белых шаров и b черных, во второй - c белых и d черных шаров, в третьей k белых шаров (черных нет). Выбирается наудачу одна из урн и из нее вынимается шар. Этот шар оказался белым. Найти вероятность того, что этот шар вынут из первой, второй или третьей урны. 61. Монета брошена N раз (N велико!). Найти вероятность того, что герб выпадет ровно N / 2 раз. 62. Производство дает 1% брака. Найти вероятность того, что из взятых для контроля 1100 деталей будет забраковано не более 17. 63. Имеется 100 станков, работающих независимо друг от друга, одинаковой мощности и одного и того же режима работы, при котором их привод включен в течение 0,8 всего рабочего времени. Найти вероятность того, что в произвольно взятый момент времени окажутся включенными от 70 до 86 станков. 64. Изделия испытываются при перегрузочных режимах. Вероятности для каждого изделия пройти испытание равны Ответы 1. 0,75. 2. 7. 1680. 8. 0,4. 9. б) б) 16. а) 17. а) 18. а)
20. а) 23. 26. 33. 36. а) 39. 42.
43. мастер не справится со своей задачей, если число неисправных авто- мобилей больше, чем заключенное в б) в) 51. 54. 0,6. 55. 58. 0,389. 59.
Указание: Так как результат опыта уже известен, следует применить фор- мулы Бейеса. Событие A – появление белого шара. Априорные гипотезы:
61. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 965; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.014 с.) |

 ).
).

 для удобства вычислений табулирована (см. приложение 1). Так как функция
для удобства вычислений табулирована (см. приложение 1). Так как функция  четная, то в таблице приведены значения
четная, то в таблице приведены значения  того, что событие A появится не менее
того, что событие A появится не менее  и не более
и не более  раз (при тех же огра-ничениях)
раз (при тех же огра-ничениях)


 называется функцией Лапласа. Она также табулирована (см. приложение 2), причем в таблице приведены значения функции Ф(x) для положительных значений аргумента. Но при пользовании таблицей следует иметь в виду, что функция Лапласа нечетная:
называется функцией Лапласа. Она также табулирована (см. приложение 2), причем в таблице приведены значения функции Ф(x) для положительных значений аргумента. Но при пользовании таблицей следует иметь в виду, что функция Лапласа нечетная: 


 Искомая вероятность равна
Искомая вероятность равна
 Найти вероятность того, что событие A появится: а) не менее 150 раз и не более 180 раз; б) не менее 150 раз; в) не более 149 раз.
Найти вероятность того, что событие A появится: а) не менее 150 раз и не более 180 раз; б) не менее 150 раз; в) не более 149 раз.





 cледовательно,
cледовательно,
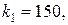



 Поэтому
Поэтому



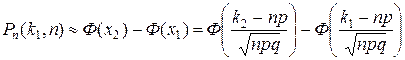
 .
. то
то  Функция Лапласа возрастающая и
Функция Лапласа возрастающая и  Поэтому можно принять
Поэтому можно принять 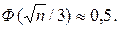 Тогда
Тогда  или
или  .
. Учитывая, что функ-ция Лапласа нечетная, получим
Учитывая, что функ-ция Лапласа нечетная, получим или
или  .
. , находим
, находим  Окончательно, требуемое количество деталей
Окончательно, требуемое количество деталей 
 - произвольное целое число.
- произвольное целое число. - верно угаданы 3 выигравших номера из 49;
- верно угаданы 3 выигравших номера из 49;  - верно угаданы 4
- верно угаданы 4 - верно угаданы 5 выигравших номера из
- верно угаданы 5 выигравших номера из - верно угаданы 6 выигравших номера из 49.
- верно угаданы 6 выигравших номера из 49. вписан круг. Наудачу брошена точка. Найти вероятность попадания точки в круг.
вписан круг. Наудачу брошена точка. Найти вероятность попадания точки в круг. Корабль летит со скоростью
Корабль летит со скоростью  км/сек. Площадь его поперечного сечения S =23 м2 . В космическом пространстве на каждые
км/сек. Площадь его поперечного сечения S =23 м2 . В космическом пространстве на каждые  км3 приходится одна опасная метеоритная частица. Какова максимально допустимая продолжительность полета корабля?
км3 приходится одна опасная метеоритная частица. Какова максимально допустимая продолжительность полета корабля? и
и  , причем
, причем  Какова вероятность того, что длина отрезка BC меньше длины отрезка OB?
Какова вероятность того, что длина отрезка BC меньше длины отрезка OB? , d)
, d)  ?
? - исправна k – ая тормозная система. Автомобиль работоспособен (событие C), если исправно рулевое управление и хотя бы одна тормозная система. Выразить события C и
- исправна k – ая тормозная система. Автомобиль работоспособен (событие C), если исправно рулевое управление и хотя бы одна тормозная система. Выразить события C и  через A и
через A и 
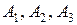 - дефекты, приводящие к опасному перегреву двигателя (
- дефекты, приводящие к опасному перегреву двигателя ( элементов, во втором -
элементов, во втором -  и в третьем
и в третьем  элементов. Для работы прибора безусловно необходим узел I; два других узла II и III дублируют друг друга (см. рис.). Вероятность работы каждого элемента одна и та же и равна p. Выход из строя одного элемента означает выход из строя всего узла. Элементы выходят из строя независимо друг от друга. Найти вероятность безотказной работы прибора.
элементов. Для работы прибора безусловно необходим узел I; два других узла II и III дублируют друг друга (см. рис.). Вероятность работы каждого элемента одна и та же и равна p. Выход из строя одного элемента означает выход из строя всего узла. Элементы выходят из строя независимо друг от друга. Найти вероятность безотказной работы прибора.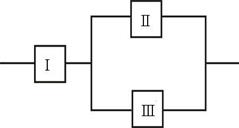
 (независимо от других) оказывается дефектным. При осмотре дефект, если он имеется, обнаруживается с вероятностью p. Для контроля из продукции завода отбираются n изделий. Найти вероятность следующих событий: A – ни в одном из изделий не будет обнаружено дефекта; B – среди n изделий ровно в двух будет обнаружен дефект; C – среди n изделий не менее чем в двух будет обнаружен дефект.
(независимо от других) оказывается дефектным. При осмотре дефект, если он имеется, обнаруживается с вероятностью p. Для контроля из продукции завода отбираются n изделий. Найти вероятность следующих событий: A – ни в одном из изделий не будет обнаружено дефекта; B – среди n изделий ровно в двух будет обнаружен дефект; C – среди n изделий не менее чем в двух будет обнаружен дефект. ?
?
 , если на ремонт каждой из неисправных автомашин ему требуется время
, если на ремонт каждой из неисправных автомашин ему требуется время 
 Если милицейская машина не подбита, то она независимо от другой стреляет по преступникам и подбивает их машину с вероятностью p. Найти вероятность того, что будет подбита: а) ровно одна машина (любая); б) хотя бы одна машина (любая).
Если милицейская машина не подбита, то она независимо от другой стреляет по преступникам и подбивает их машину с вероятностью p. Найти вероятность того, что будет подбита: а) ровно одна машина (любая); б) хотя бы одна машина (любая).

 3.
3.  4. а)
4. а)  б)
б)  5.
5.  6.
6. 
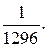 10. 0,096. 11. 0,05. 12. а)
10. 0,096. 11. 0,05. 12. а) 
 13.
13. 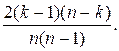 14. а)
14. а)  б)
б)  15. а)
15. а) 
 более вероятно повреждение изделий разных типов.
более вероятно повреждение изделий разных типов. б)
б) 
 б)
б) 
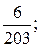 б)
б)  в)
в) 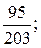 г)
г)  19.
19. 
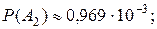


 б)
б) 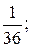 в)
в) 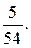 21. а)
21. а)  б)
б)  в)
в)  22.
22. 
 24.
24.  25.
25.  3 годам и 5 месяцам.
3 годам и 5 месяцам.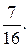 27. 0,5. 31. а)
27. 0,5. 31. а)  б)
б)  32. а) 0,6; б)
32. а) 0,6; б) 
 34. Безразлично. 35. Одинакова и равна 0,05.
34. Безразлично. 35. Одинакова и равна 0,05.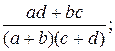 б)
б)  37.
37. 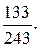 38.
38. 
 40.
40.  41.
41. 



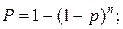
 44.
44.  Указание:
Указание: где
где  - наибольшее целое число,
- наибольшее целое число, 45. а)
45. а) 
 46. 0,784. 47. а)
46. 0,784. 47. а) 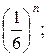 б)
б) 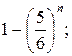
 48.
48.  49.
49. 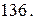 50. а)
50. а)  б)
б) 
 52.
52.  53.
53. 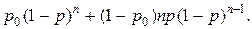
 56.
56.  57.
57. 
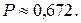 60.
60. 


 - выбор i –ой урны (i =1,2,3),
- выбор i –ой урны (i =1,2,3), 
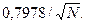 Указание: так как N велико и испытания независимы, то следует применить локальную теорему Лапласа. 62.
Указание: так как N велико и испытания независимы, то следует применить локальную теорему Лапласа. 62.  63.
63.  64. Если испытания закончатся на k – ом изделии (k =,2,3,…), то
64. Если испытания закончатся на k – ом изделии (k =,2,3,…), то 



